Biology:Circuit topology (polymers)
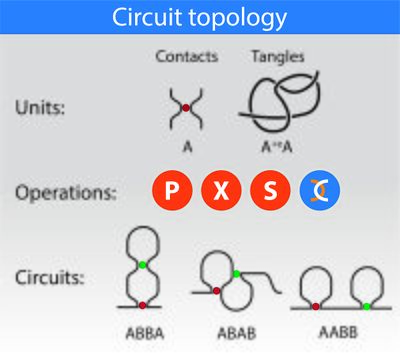
The circuit topology of a folded linear polymer refers to the arrangement of its intra-molecular contacts. Examples of linear polymers with intra-molecular contacts are nucleic acids and proteins. Proteins fold via formation of contacts of various nature, including hydrogen bonds, disulfide bonds, and beta-beta interactions.[1] RNA molecules fold by forming hydrogen bonds between nucleotides, forming nested or non-nested structures. Contacts in the genome are established via protein bridges including CTCF and cohesins and are measured by technologies including Hi-C.[2] Circuit topology categorises the topological arrangement of these physical contacts, that are referred to as hard contacts (or h-contacts). Furthermore, chains can fold via knotting (or formation of "soft" contacts (s-contacts)). Circuit topology uses a similar language to categorise both "soft" and "hard" contacts, and provides a full description of a folded linear chain. In this framework, a "circuit" refers to a segment of the chain where each contact site within the segment forms connections with other contact sites within the same segment, and thus is not left unpaired. A folded chain can thus be studied based on its constituting circuits.
A simple example of a folded chain is a chain with two hard contacts. For a chain with two binary contacts, three arrangements are available: parallel (P), series (S) and crossed (X). For a chain with n contacts, the topology can be described by an n by n matrix in which each element illustrates the relation between a pair of contacts and may take one of the three states, P, S and X. Multivalent contacts can also be categorised in full or via decomposition into several binary contacts. Similarly, circuit topology allows for classification of the pairwise arrangements of chain crossings and tangles, thus providing a complete 3D description of folded chains. Furthermore, one can apply circuit topology operations to soft and hard contacts to generate complex folds, using a bottom-up engineering approach.
Both knot theory and circuit topology aim to describe chain entanglement, making it important to understand their relationship. Knot theory considers any entangled chain as a connected sum of prime knots, which are themselves undecomposable. Circuit topology splits any entangled chains (including prime knots) into basic structural units called soft contacts, and lists simple rules how soft contacts can be put together.[3][4] An advantage of circuit topology is that it can be applied to open linear chains with intra-chain interactions, so called hard contacts.[5] This enabled topological analysis of proteins and genomes, which are often described as "unknot" in knot theory. [6] [7] Finally, circuit topology enables studying interactions between hard contacts and entanglements and is able to identify slip-knots, while knot theory typically overlooks hard contacts and split knots. Thus, circuit topology serves as a complementary approach to knot theory.
Circuit topology has implications for folding kinetics and molecular evolution and has been applied to engineer polymers including molecular origami.[8] Circuit topology along with contact order and size are determinants of folding rate of linear polymers.[9] The approach can also be used for medical applications including the prediction of pathogenicity of mutations.
Further reading
- B. Scalvini et al., Circuit topology analysis of cellular genome reveals signature motifs, conformational heterogeneity, and scaling. iScience (2022). link
- B. Scalvini et al., Topological principles of protein folding. PCCP (2021). link
- A. Golovnev at el., Generalized circuit topology of folded linear chains. iScience (2020). link
- M. Heidari et al., Circuit topology analysis of polymer folding reactions. ACS Central Science (2020) link
References
- ↑ Mashaghi, Alireza; van Wijk, Roeland J.; Tans, Sander J. (2014). "Circuit Topology of Proteins and Nucleic Acids". Structure 22 (9): 1227–1237. doi:10.1016/j.str.2014.06.015. PMID 25126961.
- ↑ Scalvini, B. et al. (2022) ‘Circuit topology analysis of cellular genome reveals signature motifs, conformational heterogeneity, and scaling’, iScience, 25(3), p. 103866.
- ↑ Golovnev A and Mashaghi A, Circuit Topology for Bottom-Up Engineering of Molecular Knots. Symmetry 2021, 13(12), 2353; https://doi.org/10.3390/sym13122353
- ↑ Flapan E et al., A tile model of circuit topology for self-entangled biopolymers Sci Rep. 2023 Jun 1;13(1):8889 https://www.nature.com/articles/s41598-023-35771-8
- ↑ A. Golovnev at el., Generalized circuit topology of folded linear chains. iScience (2020) https://www.cell.com/iscience/fulltext/S2589-0042(20)30684-2
- ↑ Yasuyuki Tezuka, Tetsuo Deguchi, Topological Polymer Chemistry: Concepts and Practices (2022) ISBN:978-981-16-6807-4
- ↑ Leiden scientists develop topological barcodes for folded molecules
- ↑ Yasuyuki Tezuka and Tetsuo Deguchi, Topological Polymer Chemistry: Concepts and Practices (2022) ISBN 978-981-16-6806-7
- ↑ Mugler, Andrew; Tans, Sander J.; Mashaghi, Alireza (2014). "Circuit topology of self-interacting chains: implications for folding and unfolding dynamics". Phys. Chem. Chem. Phys. 16 (41): 22537–22544. doi:10.1039/C4CP03402C. PMID 25228051. Bibcode: 2014PCCP...1622537M.
See also