Chemistry:ITIES
In electrochemistry, ITIES (interface between two immiscible electrolyte solutions)[1][2][3] is an electrochemical interface that is either polarisable or polarised. An ITIES is polarisable if one can change the Galvani potential difference, or in other words the difference of inner potentials between the two adjacent phases, without noticeably changing the chemical composition of the respective phases (i.e. without noticeable electrochemical reactions taking place at the interface). An ITIES system is polarised if the distribution of the different charges and redox species between the two phases determines the Galvani potential difference.
Usually, one electrolyte is an aqueous electrolyte composed of hydrophilic ions such as NaCl dissolved in water and the other electrolyte is a lipophilic salt such as tetrabutylammonium tetraphenylborate dissolved in an organic solvent immiscible with water such as nitrobenzene, or 1,2-dichloroethane.
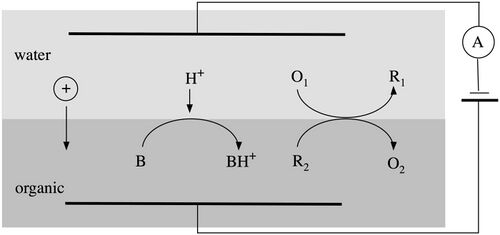
Charge transfer reactions of an ITIES
Three major classes of charge transfer reactions can be studied at an ITIES:
- Ion transfer reactions
- Assisted ion transfer reactions
- Heterogeneous electron transfer reactions
The Nernst equation for an ion transfer reaction reads
- [math]\displaystyle{ \Delta^\text{w}_\text{o}\phi = \phi^\text{w} - \phi^\text{o} = \Delta^\text{w}_\text{o}\phi^\ominus_i + \frac{RT}{z_iF}\ln\left(\frac{a^\text{o}_i}{a^\text{w}_i}\right) }[/math],
where [math]\displaystyle{ \Delta^\text{w}_\text{o}\phi^\ominus_i }[/math] is the standard transfer potential defined as the Gibbs energy of transfer expressed in a voltage scale.
- [math]\displaystyle{ \Delta^\text{w}_\text{o}\phi^\ominus_i = \frac{\Delta G^{\ominus ,\text{w}\rightarrow \text{o}}_{tr,i}}{z_iF} }[/math]
The Nernst equation for a single heterogeneous electron transfer reaction reads
- [math]\displaystyle{ \Delta^\text{w}_\text{o}\phi = \Delta^\text{w}_\text{o}\phi^\ominus_\text{ET} + \frac{RT}{F}ln\left(\frac{a^\text{w}_{\text{R}_1}a^\text{o}_{\text{O}_2}}{a^\text{w}_{\text{O}_1}a^\text{o}_{\text{R}_2}}\right) }[/math],
where [math]\displaystyle{ \Delta^\text{w}_o\phi^\ominus_\text{ET} }[/math] is the standard redox potential for the interfacial transfer of electrons defined as the difference the standard redox potentials of the two redox couples but referred to the aqueous standard hydrogen electrode (SHE).
- [math]\displaystyle{ \Delta^\text{w}_\text{o}\phi^\ominus_\text{ET} = \left[E^\ominus_{\text{O}_2/\text{R}_2}\right]^\text{o}_\text{SHE} - \left[E^\ominus_{\text{O}_1/\text{R}_1}\right]^\text{w}_\text{SHE} }[/math]
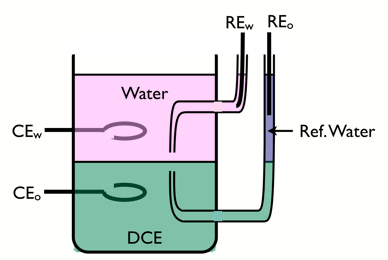
Four-electrode cell
To study charge transfer reactions of an ITIES, a four-electrode cell is used.
Two reference electrodes are used to control the polarisation of the interface, and two counter electrodes made of noble metals are used to pass the current. The aqueous supporting electrolyte must be hydrophilic, such as LiCl, and the organic electrolyte must be lipophilic, such as tetraheptylammonium tetra-pentafluorophenyl borate.
Ion partition coefficient and ion distribution coefficient
Contrary to a neutral solute, the partition coefficient of an ion depends on the Galvani potential difference between the two phases:
- [math]\displaystyle{ P_i = \frac{a^\text{o}_i}{a^\text{w}_i} = \exp \left[\frac{z_iF}{RT}(\Delta^\text{w}_\text{o}\phi - \Delta^\text{w}_\text{o}\phi^\ominus_i)\right] = P^\ominus_i \exp \left[\frac{z_iF}{RT}\Delta^\text{w}_\text{o}\phi\right] }[/math]
Distribution potential
When a salt is distributed between two phases, the Galvani potential difference is called the distribution potential and is obtained from the respective Nernst equations for the cation C+ and the anion A– to read
- [math]\displaystyle{ \Delta^\text{w}_\text{o}\phi = \frac{\Delta^\text{w}_\text{o}\phi^\ominus_\text{C+}+\Delta^\text{w}_\text{o}\phi^\ominus_\text{A-}}{2} + \frac{RT}{2F}\ln{\left(\frac{\gamma^\text{o}_\text{C+}\gamma^\text{w}_\text{A-}}{\gamma^\text{w}_\text{C+}\gamma^\text{o}_\text{A-}}\right)} }[/math]
where γ represents the activity coefficient.
See also
References
- ↑ Hung, Le Quoc (1980-12-23). "Electrochemical properties of the interface between two immiscible electrolyte solutions: Part I. Equilibrium situation and galvani potential difference". Journal of Electroanalytical Chemistry 115 (2): 159–174. doi:10.1016/S0022-0728(80)80323-8. ISSN 0022-0728.
- ↑ Hung, Le Quoc (1983-07-08). "Electrochemical properties of the interface between two immiscible electrolyte solutions: Part III. The general case of the galvani potential difference at the interface and of the distribution of an arbitrary number of components interacting in both phases". Journal of Electroanalytical Chemistry 149 (1–2): 1–14. doi:10.1016/S0022-0728(83)80553-1. ISSN 0022-0728.
- ↑ Samec, Zdenek (1988-06-01). "Electrical double layer at the interface between two immiscible electrolyte solutions". Chemical Reviews 88 (4): 617–632. doi:10.1021/cr00086a003.