Wrapped exponential distribution

Short description: Probability distribution

Wrapped Exponential

Probability density function 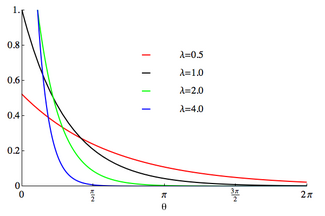The support is chosen to be [0,2π]
Cumulative distribution function 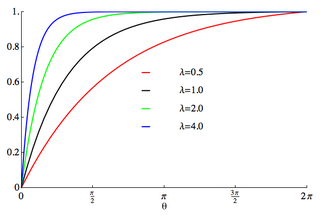The support is chosen to be [0,2π]
Parameters	[math]\displaystyle{ \lambda\gt 0 }[/math]
Support	[math]\displaystyle{ 0\le\theta\lt 2\pi }[/math]
PDF	[math]\displaystyle{ \frac{\lambda e^{-\lambda \theta}}{1-e^{-2\pi \lambda}} }[/math]
CDF	[math]\displaystyle{ \frac{1-e^{-\lambda \theta}}{1-e^{-2\pi \lambda}} }[/math]
Mean	[math]\displaystyle{ \arctan(1/\lambda) }[/math] (circular)
Variance	[math]\displaystyle{ 1-\frac{\lambda}{\sqrt{1+\lambda^2}} }[/math] (circular)
Entropy	[math]\displaystyle{ 1+\ln\left(\frac{\beta-1}{\lambda}\right)-\frac{\beta}{\beta-1}\ln(\beta) }[/math] where [math]\displaystyle{ \beta=e^{2\pi\lambda} }[/math] (differential)
CF	[math]\displaystyle{ \frac{1}{1-in/\lambda} }[/math]

In probability theory and directional statistics, a wrapped exponential distribution is a wrapped probability distribution that results from the "wrapping" of the exponential distribution around the unit circle.

Definition

The probability density function of the wrapped exponential distribution is

[math]\displaystyle{ f_{WE}(\theta;\lambda)=\sum_{k=0}^\infty \lambda e^{-\lambda (\theta+2 \pi k)}=\frac{\lambda e^{-\lambda \theta}}{1-e^{-2\pi \lambda}} , }[/math]

for [math]\displaystyle{ 0 \le \theta \lt 2\pi }[/math] where [math]\displaystyle{ \lambda \gt 0 }[/math] is the rate parameter of the unwrapped distribution. This is identical to the truncated distribution obtained by restricting observed values X from the exponential distribution with rate parameter λ to the range [math]\displaystyle{ 0\le X \lt 2\pi }[/math].

Characteristic function

The characteristic function of the wrapped exponential is just the characteristic function of the exponential function evaluated at integer arguments:

[math]\displaystyle{ \varphi_n(\lambda)=\frac{1}{1-in/\lambda} }[/math]

which yields an alternate expression for the wrapped exponential PDF in terms of the circular variable z=e ^{i (θ-m)} valid for all real θ and m:

[math]\displaystyle{ \begin{align} f_{WE}(z;\lambda) & =\frac{1}{2\pi}\sum_{n=-\infty}^\infty \frac{z^{-n}}{1-in/\lambda}\\[10pt] & = \begin{cases} \frac{\lambda}{\pi}\,\textrm{Im}(\Phi(z,1,-i\lambda))-\frac{1}{2\pi} & \text{if }z \neq 1 \\[12pt] \frac{\lambda}{1-e^{-2\pi\lambda}} & \text{if }z=1 \end{cases} \end{align} }[/math]

where [math]\displaystyle{ \Phi() }[/math] is the Lerch transcendent function.

Circular moments

In terms of the circular variable [math]\displaystyle{ z=e^{i\theta} }[/math] the circular moments of the wrapped exponential distribution are the characteristic function of the exponential distribution evaluated at integer arguments:

[math]\displaystyle{ \langle z^n\rangle=\int_\Gamma e^{in\theta}\,f_{WE}(\theta;\lambda)\,d\theta = \frac{1}{1-in/\lambda} , }[/math]

where [math]\displaystyle{ \Gamma\, }[/math] is some interval of length [math]\displaystyle{ 2\pi }[/math]. The first moment is then the average value of z, also known as the mean resultant, or mean resultant vector:

[math]\displaystyle{ \langle z \rangle=\frac{1}{1-i/\lambda} . }[/math]

The mean angle is

[math]\displaystyle{ \langle \theta \rangle=\mathrm{Arg}\langle z \rangle = \arctan(1/\lambda) , }[/math]

and the length of the mean resultant is

[math]\displaystyle{ R=|\langle z \rangle| = \frac{\lambda}{\sqrt{1+\lambda^2}} . }[/math]

and the variance is then 1-R.

Characterisation

The wrapped exponential distribution is the maximum entropy probability distribution for distributions restricted to the range [math]\displaystyle{ 0\le \theta \lt 2\pi }[/math] for a fixed value of the expectation [math]\displaystyle{ \operatorname{E}(\theta) }[/math].

See also

• Wrapped distribution
• Directional statistics