Matroid polytope
In mathematics, a matroid polytope, also called a matroid basis polytope (or basis matroid polytope) to distinguish it from other polytopes derived from a matroid, is a polytope constructed via the bases of a matroid. Given a matroid [math]\displaystyle{ M }[/math], the matroid polytope [math]\displaystyle{ P_M }[/math] is the convex hull of the indicator vectors of the bases of [math]\displaystyle{ M }[/math].
Definition
Let [math]\displaystyle{ M }[/math] be a matroid on [math]\displaystyle{ n }[/math] elements. Given a basis [math]\displaystyle{ B \subseteq \{1,\dots, n\} }[/math] of [math]\displaystyle{ M }[/math], the indicator vector of [math]\displaystyle{ B }[/math] is
- [math]\displaystyle{ \mathbf e_B := \sum_{i \in B} \mathbf e_i, }[/math]
where [math]\displaystyle{ \mathbf e_i }[/math] is the standard [math]\displaystyle{ i }[/math]th unit vector in [math]\displaystyle{ \mathbb{R}^n }[/math]. The matroid polytope [math]\displaystyle{ P_M }[/math] is the convex hull of the set
- [math]\displaystyle{ \{\mathbf e_B \mid B \text{ is a basis of } M\} \subseteq \mathbb{R}^n. }[/math]
Examples
- Let [math]\displaystyle{ M }[/math] be the rank 2 matroid on 4 elements with bases
- [math]\displaystyle{ \mathcal{B}(M) = \{\{1,2\},\{1,3\},\{1,4\},\{2,3\},\{2,4\}\}. }[/math]
- That is, all 2-element subsets of [math]\displaystyle{ \{1,2,3,4\} }[/math] except [math]\displaystyle{ \{3,4\} }[/math]. The corresponding indicator vectors of [math]\displaystyle{ \mathcal{B}(M) }[/math] are
- [math]\displaystyle{ \{\{1,1,0,0\}, \{1,0,1,0\}, \{1,0,0,1\}, \{0,1,1,0\}, \{0,1,0,1\}\}. }[/math]
- The matroid polytope of [math]\displaystyle{ M }[/math] is
- [math]\displaystyle{ P_M = \text{conv}\{\{1,1,0,0\}, \{1,0,1,0\}, \{1,0,0,1\}, \{0,1,1,0\}, \{0,1,0,1\}\}. }[/math]
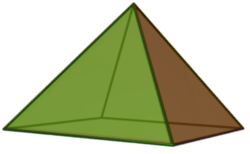
- These points form four equilateral triangles at point [math]\displaystyle{ \{1,1,0,0\} }[/math], therefore its convex hull is the square pyramid by definition.
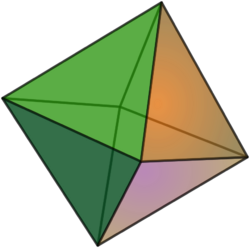
- Let [math]\displaystyle{ N }[/math] be the rank 2 matroid on 4 elements with bases that are all 2-element subsets of [math]\displaystyle{ \{1,2,3,4\} }[/math]. The corresponding matroid polytope [math]\displaystyle{ P_N }[/math] is the octahedron. Observe that the polytope [math]\displaystyle{ P_M }[/math] from the previous example is contained in [math]\displaystyle{ P_N }[/math].
- If [math]\displaystyle{ M }[/math] is the uniform matroid of rank [math]\displaystyle{ r }[/math] on [math]\displaystyle{ n }[/math] elements, then the matroid polytope [math]\displaystyle{ P_M }[/math] is the hypersimplex [math]\displaystyle{ \Delta_n^r }[/math].[1]
Properties
- A matroid polytope is contained in the hypersimplex [math]\displaystyle{ \Delta_n^r }[/math], where [math]\displaystyle{ r }[/math] is the rank of the associated matroid and [math]\displaystyle{ n }[/math] is the size of the ground set of the associated matroid.[2] Moreover, the vertices of [math]\displaystyle{ P_M }[/math] are a subset of the vertices of [math]\displaystyle{ \Delta_n^r }[/math].
- Every edge of a matroid polytope [math]\displaystyle{ P_M }[/math] is a parallel translate of [math]\displaystyle{ e_i-e_j }[/math] for some [math]\displaystyle{ i,j\in E }[/math], the ground set of the associated matroid. In other words, the edges of [math]\displaystyle{ P_M }[/math] correspond exactly to the pairs of bases [math]\displaystyle{ B, B' }[/math] that satisfy the basis exchange property: [math]\displaystyle{ B' = B\setminus{i\cup j} }[/math] for some [math]\displaystyle{ i,j\in E. }[/math][2] Because of this property, every edge length is the square root of two. More generally, the families of sets for which the convex hull of indicator vectors has edge lengths one or the square root of two are exactly the delta-matroids.
- Matroid polytopes are members of the family of generalized permutohedra.[3]
- Let [math]\displaystyle{ r:2^E \rightarrow \mathbb{Z} }[/math] be the rank function of a matroid [math]\displaystyle{ M }[/math]. The matroid polytope [math]\displaystyle{ P_M }[/math] can be written uniquely as a signed Minkowski sum of simplices:[3]
- [math]\displaystyle{ P_M = \sum_{A\subseteq E} \tilde{\beta}(M/A) \Delta_{E-A} }[/math]
- where [math]\displaystyle{ E }[/math] is the ground set of the matroid [math]\displaystyle{ M }[/math] and [math]\displaystyle{ \beta(M) }[/math] is the signed beta invariant of [math]\displaystyle{ M }[/math]:
- [math]\displaystyle{ \tilde{\beta}(M) = (-1)^{r(M)+1}\beta(M), }[/math]
- [math]\displaystyle{ \beta(M) = (-1)^{r(M)} \sum_{X\subseteq E} (-1)^{|X|}r(X). }[/math]
- [math]\displaystyle{ P_M:= \left\{\textbf{x}\in \mathbb{R}_+^E~|~\sum_{e\in U}\textbf{x}(e)\leq r(U), \forall U\subseteq E\right\} }[/math]
Related polytopes
Independence matroid polytope
The matroid independence polytope or independence matroid polytope is the convex hull of the set
- [math]\displaystyle{ \{\, \mathbf e_I \mid I \text{ is an independent set of } M \,\} \subseteq \mathbb R^n. }[/math]
The (basis) matroid polytope is a face of the independence matroid polytope. Given the rank [math]\displaystyle{ \psi }[/math] of a matroid [math]\displaystyle{ M }[/math], the independence matroid polytope is equal to the polymatroid determined by [math]\displaystyle{ \psi }[/math].
Flag matroid polytope
The flag matroid polytope is another polytope constructed from the bases of matroids. A flag [math]\displaystyle{ \mathcal{F} }[/math] is a strictly increasing sequence
- [math]\displaystyle{ F^1 \subset F^2\subset \cdots \subset F^m \, }[/math]
of finite sets.[4] Let [math]\displaystyle{ k_i }[/math] be the cardinality of the set [math]\displaystyle{ F_i }[/math]. Two matroids [math]\displaystyle{ M }[/math] and [math]\displaystyle{ N }[/math] are said to be concordant if their rank functions satisfy
- [math]\displaystyle{ r_M(Y) - r_M(X) \leq r_N(Y) - r_N(X) \text{ for all } X\subset Y \subseteq E. \, }[/math]
Given pairwise concordant matroids [math]\displaystyle{ M_1,\dots,M_m }[/math] on the ground set [math]\displaystyle{ E }[/math] with ranks [math]\displaystyle{ r_1\lt \cdots \lt r_m }[/math], consider the collection of flags [math]\displaystyle{ (B_1,\dots, B_m) }[/math] where [math]\displaystyle{ B_i }[/math] is a basis of the matroid [math]\displaystyle{ M_i }[/math] and [math]\displaystyle{ B_1 \subset \cdots\subset B_m }[/math]. Such a collection of flags is a flag matroid [math]\displaystyle{ \mathcal{F} }[/math]. The matroids [math]\displaystyle{ M_1,\dots,M_m }[/math] are called the constituents of [math]\displaystyle{ \mathcal{F} }[/math]. For each flag [math]\displaystyle{ B=(B_1,\dots,B_m) }[/math] in a flag matroid [math]\displaystyle{ \mathcal{F} }[/math], let [math]\displaystyle{ v_B }[/math] be the sum of the indicator vectors of each basis in [math]\displaystyle{ B }[/math]
- [math]\displaystyle{ v_B = v_{B_1}+\cdots+v_{B_m}. \, }[/math]
Given a flag matroid [math]\displaystyle{ \mathcal{F} }[/math], the flag matroid polytope [math]\displaystyle{ P_\mathcal{F} }[/math] is the convex hull of the set
- [math]\displaystyle{ \{v_B \mid B\text{ is a flag in }\mathcal{F}\}. }[/math]
A flag matroid polytope can be written as a Minkowski sum of the (basis) matroid polytopes of the constituent matroids:[4]
- [math]\displaystyle{ P_\mathcal{F} = P_{M_1} + \cdots + P_{M_k}. \, }[/math]
References
- ↑ "Cardinality homogeneous set systems, cycles in matroids, and associated polytopes", The Sharpest Cut: The Impact of Manfred Padberg and His Work, MPS/SIAM Ser. Optim., SIAM, Philadelphia, PA, 2004, pp. 99–120. See in particular the remarks following Prop. 8.20 on p. 114.
- ↑ 2.0 2.1 Gelfand, I.M.; Goresky, R.M.; MacPherson, R.D.; Serganova, V.V. (1987). "Combinatorial geometries, convex polyhedra, and Schubert cells". Advances in Mathematics 63 (3): 301–316. doi:10.1016/0001-8708(87)90059-4.
- ↑ 3.0 3.1 Ardila, Federico; Benedetti, Carolina; Doker, Jeffrey (2010). "Matroid polytopes and their volumes". Discrete & Computational Geometry 43 (4): 841–854. doi:10.1007/s00454-009-9232-9.
- ↑ 4.0 4.1 Borovik, Alexandre V.; Gelfand, I.M.; White, Neil (2013). "Coxeter Matroids". Progress in Mathematics 216. doi:10.1007/978-1-4612-2066-4.
 |