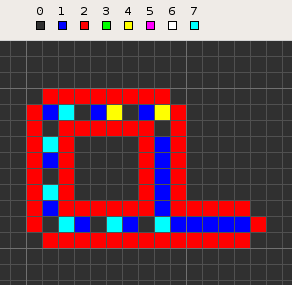
Langton's loops
Langton's loops are a particular "species" of artificial life in a cellular automaton created in 1984 by Christopher Langton. They consist of a loop of cells containing genetic information, which flows continuously around the loop and out along an "arm" (or pseudopod), which will become the daughter loop. The "genes" instruct it to make three left turns, completing the loop, which then disconnects from its parent.
History
In 1952 John von Neumann created the first cellular automaton (CA) with the goal of creating a self-replicating machine.[1] This automaton was necessarily very complex due to its computation- and construction-universality. In 1968 Edgar F. Codd reduced the number of states from 29 in von Neumann's CA to 8 in his.[2] When Christopher Langton did away with the universality condition, he was able to significantly reduce the automaton's complexity. Its self-replicating loops are based on one of the simplest elements in Codd's automaton, the periodic emitter.
Specification
Langton's Loops run in a CA that has 8 states, and uses the von Neumann neighborhood with rotational symmetry. The transition table can be found here: [1].
As with Codd's CA, Langton's Loops consist of sheathed wires. The signals travel passively along the wires until they reach the open ends, when the command they carry is executed.
Colonies
Because of a particular property of the loops' "pseudopodia", they are unable to reproduce into the space occupied by another loop. Thus, once a loop is surrounded, it is incapable of reproducing, resulting in a coral-like colony with a thin layer of reproducing organisms surrounding a core of inactive "dead" organisms. Unless provided unbounded space, the colony's size will be limited. The maximum population will be asymptotic to [math]\displaystyle{ \textstyle \left \lfloor \frac{A}{121} \right \rfloor }[/math], where A is the total area of the space in cells.
Encoding of the genome
The loops' genetic code is stored as a series of nonzero-zero state pairs. The standard loop's genome is illustrated in the picture at the top, and may be stated as a series of numbered states starting from the T-junction and running clockwise: 70-70-70-70-70-70-40-40. The '70' command advances the end of the wire by one cell, while the '40-40' sequence causes the left turn. State 3 is used as a temporary marker for several stages.
While the roles of states 0,1,2,3,4 and 7 are similar to Codd's CA, the remaining states 5 and 6 are used instead to mediate the loop replication process. After the loop has completed, state 5 travels counter-clockwise along the sheath of the parent loop to the next corner, causing the next arm to be produced in a different direction. State 6 temporarily joins the genome of the daughter loop and initialises the growing arm at the next corner it reaches.
The genome is used a total of six times: once to extend the pseudopod to the desired location, four times to complete the loop, and again to transfer the genome into the daughter loop. Clearly, this is dependent on the fourfold rotational symmetry of the loop; without it, the loop would be incapable of containing the information required to describe it. The same use of symmetry for genome compression is used in many biological viruses, such as the icosahedral adenovirus.
| CA | number of states | neighborhood | number of cells (typical) | replication period (typical) | thumbnail |
|---|---|---|---|---|---|
| Langton's loops[3] (1984): The original self-reproducing loop. | 8 | von Neumann | 86 | 151 | |
| Byl's loop[4] (1989): By removing the inner sheath, Byl reduced the size of the loop. | 6 | von Neumann | 12 | 25 | |
| Chou-Reggia loop[5] (1993): A further reduction of the loop by removing all sheaths. | 8 | von Neumann | 5 | 15 | |
| Tempesti loop[6] (1995): Tempesti added construction capabilities to his loop, allowing patterns to be written inside the loop after reproduction. | 10 | Moore | 148 | 304 | |
| Perrier loop[7] (1996): Perrier added a program stack and an extensible data tape to Langton's loop, allowing it to compute anything computable. | 64 | von Neumann | 158 | 235 | |
| SDSR loop[8] (1998): With an extra structure-dissolving state added to Langton's loops, the SDSR loop has a limited lifetime and dissolves at the end of its life cycle. This allows continuous growth and turn-over of generations. | 9 | von Neumann | 86 | 151 | |
| Evoloop[9] (1999): An extension of the SDSR loop, Evoloop is capable of interaction with neighboring loops as well as of evolution. Often, the greatest selection pressure in a colony of Evoloops is the competition for space, and natural selection favors the smallest functional loop present. Further studies demonstrated more complexity than originally thought in the Evoloop system.[10] | 9 | von Neumann | 149 | 363 | |
| Sexyloop[11] (2007): Sexyloop is a modification of the Evoloop where self-reproducing loops have the capability of sex. With this ability, the loops are capable of transferring genetic material into other loops. This increases diversity in the evolution of new species of loops. | 10 | von Neumann | 149 | 363 |
See also
- Artificial life – Field of study
- Cellular automaton – Discrete model studied in computer science
- Biography:Christopher Langton – American computer scientist
- Codd's cellular automaton – 2D cellular automaton devised by Edgar F. Codd in 1968
- Conway's Game of Life – Two-dimensional cellular automaton devised by J. H. Conway in 1970
- Langton's ant – Two-dimensional Turing machine with emergent behavior
- Von Neumann cellular automaton – Cellular automaton used to model universal construction
References
- ↑ von Neumann, John; Burks, Arthur W. (1966). "Theory of Self-Reproducing Automata." (Scanned book online). www.walenz.org. http://www.walenz.org/vonNeumann/index.html.
- ↑ Codd, Edgar F. (1968). Cellular Automata. Academic Press, New York.
- ↑ C. G. Langton (1984). "Self-reproduction in cellular automata". Physica D 10 (1–2): 135–144. doi:10.1016/0167-2789(84)90256-2. https://deepblue.lib.umich.edu/bitstream/2027.42/24968/1/0000395.pdf.
- ↑ J. Byl (1989). "Self-Reproduction in small cellular automata". Physica D 34 (1–2): 295–299. doi:10.1016/0167-2789(89)90242-X.
- ↑ J. A. Reggia; S. L. Armentrout; H.-H. Chou; Y. Peng (1993). "Simple systems that exhibit self-directed replication". Science 259 (5099): 1282–1287. doi:10.1126/science.259.5099.1282. PMID 17732248.
- ↑ G. Tempesti (1995). "A New Self-Reproducing Cellular Automaton Capable of Construction and Computation". Granada, Spain: Lecture Notes in Artificial Intelligence, 929, Springer Verlag, Berlin. pp. 555–563.
- ↑ J.-Y. Perrier; M. Sipper; J. Zahnd (1996). "Toward a viable, self-reproducing universal computer". Physica D 97 (4): 335–352. doi:10.1016/0167-2789(96)00091-7.
- ↑ Sayama, Hiroki (1998). "Introduction of Structural Dissolution into Langton's Self-Reproducing Loop". Los Angeles, California: MIT Press. pp. 114–122. http://cseweb.ucsd.edu/~rik/alife6/papers/IN79.html.
- ↑ Sayama, Hiroki (1999). "Toward the Realization of an Evolving Ecosystem on Cellular Automata". Beppu, Oita, Japan. pp. 254–257.
- ↑ Chris Salzberg; Hiroki Sayama (2004). "Complex genetic evolution of artificial self-replicators in cellular automata". Complexity 10 (2): 33–39. doi:10.1002/cplx.20060. http://www3.interscience.wiley.com/journal/109860047/abstract.
- ↑ Nicolas Oros; C. L. Nehaniv (2007). "Sexyloop: Self-Reproduction, Evolution and Sex in Cellular Automata". pp. 130–138.
External links
- Video of Chris Langton demonstrating self reproducing loops.
- visual representation of several of the self-replicating loops in a Java applet
- The Rule Table Repository has the transition tables for many of the CA mentioned above.
- Golly - supports Langton's Loops along with the Game of Life, and other rulesets.
 |