Richmond surface
From HandWiki
Revision as of 22:18, 13 June 2021 by imported>Jport (url)
Short description: Minimal surface in differential geometry
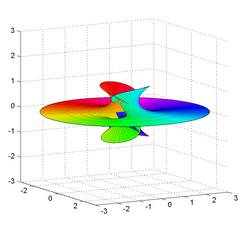
In differential geometry, a Richmond surface is a minimal surface first described by Herbert William Richmond in 1904. [1] It is a family of surfaces with one planar end and one Enneper surface-like self-intersecting end.
It has Weierstrass–Enneper parameterization [math]\displaystyle{ f(z)=1/z^2, g(z)=z^m }[/math]. This allows a parametrization based on a complex parameter as
- [math]\displaystyle{ \begin{align} X(z) &= \Re[(-1/2z) - z^{2m+1}/(4m+2)]\\ Y(z) &= \Re[(-i/2z) + i z^{2m+1}/(4m+2)]\\ Z(z) &= \Re[z^m / m] \end{align} }[/math]
The associate family of the surface is just the surface rotated around the z-axis.
Taking m = 2 a real parametric expression becomes:[2]
- [math]\displaystyle{ \begin{align} X(u,v) &= (1/3)u^3 - uv^2 + \frac{u}{u^2+v^2}\\ Y(u,v) &= -u^2v + (1/3)v^3 - \frac{v}{u^2+v^2}\\ Z(u,v) &= 2u \end{align} }[/math]
References
- ↑ Jesse Douglas, Tibor Radó, The Problem of Plateau: A Tribute to Jesse Douglas & Tibor Radó, World Scientific, 1992 (p. 239-240)
- ↑ John Oprea, The Mathematics of Soap Films: Explorations With Maple, American Mathematical Soc., 2000
 |