Bivariate von Mises distribution
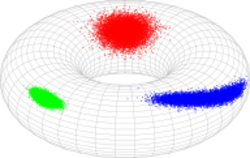
In probability theory and statistics, the bivariate von Mises distribution is a probability distribution describing values on a torus. It may be thought of as an analogue on the torus of the bivariate normal distribution. The distribution belongs to the field of directional statistics. The general bivariate von Mises distribution was first proposed by Kanti Mardia in 1975.[1][2] One of its variants is today used in the field of bioinformatics to formulate a probabilistic model of protein structure in atomic detail, [3][4] such as backbone-dependent rotamer libraries.
Definition
The bivariate von Mises distribution is a probability distribution defined on the torus, [math]\displaystyle{ S^1 \times S^1 }[/math] in [math]\displaystyle{ \mathbb{R}^3 }[/math]. The probability density function of the general bivariate von Mises distribution for the angles [math]\displaystyle{ \phi, \psi \in [0, 2\pi] }[/math] is given by[1]
- [math]\displaystyle{ f(\phi, \psi) \propto \exp [ \kappa_1 \cos(\phi - \mu) + \kappa_2 \cos(\psi - \nu) + (\cos(\phi-\mu), \sin(\phi-\mu)) \mathbf{A} (\cos(\psi - \nu), \sin(\psi - \nu))^T ], }[/math]
where [math]\displaystyle{ \mu }[/math] and [math]\displaystyle{ \nu }[/math] are the means for [math]\displaystyle{ \phi }[/math] and [math]\displaystyle{ \psi }[/math], [math]\displaystyle{ \kappa_1 }[/math] and [math]\displaystyle{ \kappa_2 }[/math] their concentration and the matrix [math]\displaystyle{ \mathbf{A} \in \mathbb{M}(2,2) }[/math] is related to their correlation.
Two commonly used variants of the bivariate von Mises distribution are the sine and cosine variant.
The cosine variant of the bivariate von Mises distribution[3] has the probability density function
- [math]\displaystyle{ f(\phi, \psi) = Z_c(\kappa_1, \kappa_2, \kappa_3) \ \exp [ \kappa_1 \cos(\phi - \mu) + \kappa_2 \cos(\psi - \nu) - \kappa_3 \cos(\phi - \mu - \psi + \nu) ], }[/math]
where [math]\displaystyle{ \mu }[/math] and [math]\displaystyle{ \nu }[/math] are the means for [math]\displaystyle{ \phi }[/math] and [math]\displaystyle{ \psi }[/math], [math]\displaystyle{ \kappa_1 }[/math] and [math]\displaystyle{ \kappa_2 }[/math] their concentration and [math]\displaystyle{ \kappa_3 }[/math] is related to their correlation. [math]\displaystyle{ Z_c }[/math] is the normalization constant. This distribution with [math]\displaystyle{ \kappa_3 }[/math]=0 has been used for kernel density estimates of the distribution of the protein dihedral angles [math]\displaystyle{ \phi }[/math] and [math]\displaystyle{ \psi }[/math].[4]
The sine variant has the probability density function[5]
- [math]\displaystyle{ f(\phi, \psi) = Z_s(\kappa_1, \kappa_2, \kappa_3) \ \exp [ \kappa_1 \cos(\phi - \mu) + \kappa_2 \cos(\psi - \nu) + \kappa_3 \sin(\phi - \mu) \sin(\psi - \nu) ], }[/math]
where the parameters have the same interpretation.
See also
- Von Mises distribution, a similar distribution on the one-dimensional unit circle
- Kent distribution, a related distribution on the two-dimensional unit sphere
- von Mises–Fisher distribution
- Directional statistics
References
- ↑ 1.0 1.1 Mardia, Kanti (1975). "Statistics of directional data". J. R. Stat. Soc. B 37 (3): 349–393.
- ↑ Mardia, K. V.; Frellsen, J. (2012). "Statistics of Bivariate von Mises Distributions". Bayesian Methods in Structural Bioinformatics. Statistics for Biology and Health. pp. 159. doi:10.1007/978-3-642-27225-7_6. ISBN 978-3-642-27224-0. https://archive.org/details/bayesianmethodss00hame.
- ↑ 3.0 3.1 Boomsma, W.; Mardia, K. V.; Taylor, C. C.; Ferkinghoff-Borg, J.; Krogh, A.; Hamelryck, T. (2008). "A generative, probabilistic model of local protein structure". Proceedings of the National Academy of Sciences 105 (26): 8932–7. doi:10.1073/pnas.0801715105. PMID 18579771. Bibcode: 2008PNAS..105.8932B.
- ↑ 4.0 4.1 "A smoothed backbone-dependent rotamer library for proteins derived from adaptive kernel density estimates and regressions". Structure 19 (6): 844–858. 2011. doi:10.1016/j.str.2011.03.019. PMID 21645855.
- ↑ Singh, H. (2002). "Probabilistic model for two dependent circular variables". Biometrika 89 (3): 719–723. doi:10.1093/biomet/89.3.719.
 |

