Multivariate normal distribution

Short description: Generalization of the one-dimensional normal distribution to higher dimensions

Multivariate normal

Probability density function 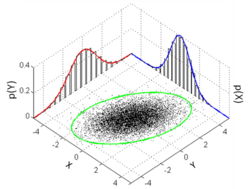Many sample points from a multivariate normal distribution with [math]\displaystyle{ \boldsymbol\mu = \left[\begin{smallmatrix}0 \\ 0\end{smallmatrix}\right] }[/math] and [math]\displaystyle{ \boldsymbol\Sigma = \left[\begin{smallmatrix}1 & 3/5 \\ 3/5 & 2\end{smallmatrix}\right] }[/math], shown along with the 3-sigma ellipse, the two marginal distributions, and the two 1-d histograms.
Notation	[math]\displaystyle{ \mathcal{N}(\boldsymbol\mu,\, \boldsymbol\Sigma) }[/math]
Parameters	μ ∈ Rk — location Σ ∈ Rk × k — covariance (positive semi-definite matrix)
Support	x ∈ μ + span(Σ) ⊆ Rk
PDF	[math]\displaystyle{ (2\pi)^{-k/2}\det (\boldsymbol\Sigma)^{-1/2} \, \exp \left( -\frac{1}{2} (\mathbf{x} - \boldsymbol\mu)^\mathrm{T} \boldsymbol\Sigma^{-1}(\mathbf{x} - \boldsymbol\mu) \right), }[/math] exists only when Σ is positive-definite
Mean	μ
Mode	μ
Variance	Σ
Entropy	[math]\displaystyle{ \frac{k}{2} \log \mathord\left( 2\pi \mathrm{e} \right) + \frac{1}{2} \log \det\mathord\left( \boldsymbol\Sigma \right) }[/math]
MGF	[math]\displaystyle{ \exp\!\Big( \boldsymbol\mu^\mathrm{T} \mathbf{t} + \tfrac{1}{2} \mathbf{t}^\mathrm{T} \boldsymbol\Sigma \mathbf{t}\Big) }[/math]
CF	[math]\displaystyle{ \exp\!\Big( i\boldsymbol\mu^\mathrm{T} \mathbf{t} - \tfrac{1}{2} \mathbf{t}^\mathrm{T} \boldsymbol\Sigma \mathbf{t}\Big) }[/math]
Kullback-Leibler divergence	See § Kullback–Leibler divergence

In probability theory and statistics, the multivariate normal distribution, multivariate Gaussian distribution, or joint normal distribution is a generalization of the one-dimensional (univariate) normal distribution to higher dimensions. One definition is that a random vector is said to be k-variate normally distributed if every linear combination of its k components has a univariate normal distribution. Its importance derives mainly from the multivariate central limit theorem. The multivariate normal distribution is often used to describe, at least approximately, any set of (possibly) correlated real-valued random variables each of which clusters around a mean value.

Definitions

Notation and parametrization

The multivariate normal distribution of a k-dimensional random vector [math]\displaystyle{ \mathbf{X} = (X_1,\ldots,X_k)^{\mathrm T} }[/math] can be written in the following notation:

[math]\displaystyle{ \mathbf{X}\ \sim\ \mathcal{N}(\boldsymbol\mu,\, \boldsymbol\Sigma), }[/math]

or to make it explicitly known that X is k-dimensional,

[math]\displaystyle{ \mathbf{X}\ \sim\ \mathcal{N}_k(\boldsymbol\mu,\, \boldsymbol\Sigma), }[/math]

with k-dimensional mean vector

[math]\displaystyle{ \boldsymbol\mu = \operatorname{E}[\mathbf{X}] = ( \operatorname{E}[X_1], \operatorname{E}[X_2], \ldots, \operatorname{E}[X_k] ) ^ \mathrm{T}, }[/math]

and [math]\displaystyle{ k \times k }[/math] covariance matrix

[math]\displaystyle{ \Sigma_{i,j} = \operatorname{E} [(X_i - \mu_i)( X_j - \mu_j)] = \operatorname{Cov}[X_i, X_j] }[/math]

such that [math]\displaystyle{ 1 \le i \le k }[/math] and [math]\displaystyle{ 1 \le j \le k }[/math]. The inverse of the covariance matrix is called the precision matrix, denoted by [math]\displaystyle{ \boldsymbol{Q}=\boldsymbol\Sigma^{-1} }[/math].

Standard normal random vector

A real random vector [math]\displaystyle{ \mathbf{X} = (X_1,\ldots,X_k)^{\mathrm T} }[/math] is called a standard normal random vector if all of its components [math]\displaystyle{ X_i }[/math] are independent and each is a zero-mean unit-variance normally distributed random variable, i.e. if [math]\displaystyle{ X_i \sim\ \mathcal{N}(0,1) }[/math] for all [math]\displaystyle{ i=1\ldots k }[/math].

Centered normal random vector

A real random vector [math]\displaystyle{ \mathbf{X} = (X_1,\ldots,X_k)^{\mathrm T} }[/math] is called a centered normal random vector if there exists a deterministic [math]\displaystyle{ k \times \ell }[/math] matrix [math]\displaystyle{ \boldsymbol{A} }[/math] such that [math]\displaystyle{ \boldsymbol{A} \mathbf{Z} }[/math] has the same distribution as [math]\displaystyle{ \mathbf{X} }[/math] where [math]\displaystyle{ \mathbf{Z} }[/math] is a standard normal random vector with [math]\displaystyle{ \ell }[/math] components.

Normal random vector

A real random vector [math]\displaystyle{ \mathbf{X} = (X_1,\ldots,X_k)^{\mathrm T} }[/math] is called a normal random vector if there exists a random [math]\displaystyle{ \ell }[/math]-vector [math]\displaystyle{ \mathbf{Z} }[/math], which is a standard normal random vector, a [math]\displaystyle{ k }[/math]-vector [math]\displaystyle{ \mathbf{\mu} }[/math], and a [math]\displaystyle{ k \times \ell }[/math] matrix [math]\displaystyle{ \boldsymbol{A} }[/math], such that [math]\displaystyle{ \mathbf{X}=\boldsymbol{A} \mathbf{Z} + \mathbf{\mu} }[/math].

Formally:

[math]\displaystyle{ \mathbf{X}\ \sim\ \mathcal{N}(\mathbf{\mu}, \boldsymbol\Sigma) \quad \iff \quad \text{there exist } \mathbf{\mu}\in\mathbb{R}^k,\boldsymbol{A}\in\mathbb{R}^{k\times \ell} \text{ such that } \mathbf{X}=\boldsymbol{A} \mathbf{Z} + \mathbf{\mu} \text{ and } \forall n=1,\ldots,l : Z_n \sim\ \mathcal{N}(0, 1), \text{i.i.d.} }[/math]

Here the covariance matrix is [math]\displaystyle{ \boldsymbol\Sigma = \boldsymbol{A} \boldsymbol{A}^{\mathrm T} }[/math].

In the degenerate case where the covariance matrix is singular, the corresponding distribution has no density; see the section below for details. This case arises frequently in statistics; for example, in the distribution of the vector of residuals in the ordinary least squares regression. The [math]\displaystyle{ X_i }[/math] are in general not independent; they can be seen as the result of applying the matrix [math]\displaystyle{ \boldsymbol{A} }[/math] to a collection of independent Gaussian variables [math]\displaystyle{ \mathbf{Z} }[/math].

Equivalent definitions

The following definitions are equivalent to the definition given above. A random vector [math]\displaystyle{ \mathbf{X} = (X_1, \ldots, X_k)^\mathrm{T} }[/math] has a multivariate normal distribution if it satisfies one of the following equivalent conditions.

• Every linear combination [math]\displaystyle{ Y=a_1 X_1 + \cdots + a_k X_k }[/math] of its components is normally distributed. That is, for any constant vector [math]\displaystyle{ \mathbf{a} \in \mathbb{R}^k }[/math], the random variable [math]\displaystyle{ Y=\mathbf{a}^{\mathrm T}\mathbf{X} }[/math] has a univariate normal distribution, where a univariate normal distribution with zero variance is a point mass on its mean.
• There is a k-vector [math]\displaystyle{ \mathbf{\mu} }[/math] and a symmetric, positive semidefinite [math]\displaystyle{ k \times k }[/math] matrix [math]\displaystyle{ \boldsymbol\Sigma }[/math], such that the characteristic function of [math]\displaystyle{ \mathbf{X} }[/math] is [math]\displaystyle{ \varphi_\mathbf{X}(\mathbf{u}) = \exp\Big( i\mathbf{u}^\mathrm{T}\boldsymbol\mu - \tfrac{1}{2} \mathbf{u}^\mathrm{T}\boldsymbol\Sigma \mathbf{u} \Big). }[/math]

The spherical normal distribution can be characterised as the unique distribution where components are independent in any orthogonal coordinate system.

Density function

Bivariate normal joint density

Non-degenerate case

The multivariate normal distribution is said to be "non-degenerate" when the symmetric covariance matrix [math]\displaystyle{ \boldsymbol\Sigma }[/math] is positive definite. In this case the distribution has density

[math]\displaystyle{ f_{\mathbf X}(x_1,\ldots,x_k) = \frac{\exp\left(-\frac 1 2 \left({\mathbf x} - {\boldsymbol\mu}\right)^\mathrm{T}{\boldsymbol\Sigma}^{-1}\left({\mathbf x}-{\boldsymbol\mu}\right)\right)}{\sqrt{(2\pi)^k |\boldsymbol\Sigma|}} }[/math]

where [math]\displaystyle{ {\mathbf x} }[/math] is a real k-dimensional column vector and [math]\displaystyle{ |\boldsymbol\Sigma|\equiv \det\boldsymbol\Sigma }[/math] is the determinant of [math]\displaystyle{ \boldsymbol\Sigma }[/math], also known as the generalized variance. The equation above reduces to that of the univariate normal distribution if [math]\displaystyle{ \boldsymbol\Sigma }[/math] is a [math]\displaystyle{ 1 \times 1 }[/math] matrix (i.e. a single real number).

The circularly symmetric version of the complex normal distribution has a slightly different form.

Each iso-density locus — the locus of points in k-dimensional space each of which gives the same particular value of the density — is an ellipse or its higher-dimensional generalization; hence the multivariate normal is a special case of the elliptical distributions.

The quantity [math]\displaystyle{ \sqrt{({\mathbf x}-{\boldsymbol\mu})^\mathrm{T}{\boldsymbol\Sigma}^{-1}({\mathbf x}-{\boldsymbol\mu})} }[/math] is known as the Mahalanobis distance, which represents the distance of the test point [math]\displaystyle{ {\mathbf x} }[/math] from the mean [math]\displaystyle{ {\boldsymbol\mu} }[/math]. Note that in the case when [math]\displaystyle{ k = 1 }[/math], the distribution reduces to a univariate normal distribution and the Mahalanobis distance reduces to the absolute value of the standard score. See also Interval below.

Bivariate case

In the 2-dimensional nonsingular case ([math]\displaystyle{ k = \operatorname{rank}\left(\Sigma\right) = 2 }[/math]), the probability density function of a vector [math]\displaystyle{ \text{[XY]′} }[/math] is: [math]\displaystyle{ f(x,y) = \frac{1}{2 \pi \sigma_X \sigma_Y \sqrt{1-\rho^2}} \exp \left( -\frac{1}{2\left[1 - \rho^2\right]}\left[ \left(\frac{x-\mu_X}{\sigma_X}\right)^2 - 2\rho\left(\frac{x - \mu_X}{\sigma_X}\right)\left(\frac{y - \mu_Y}{\sigma_Y}\right) + \left(\frac{y - \mu_Y}{\sigma_Y}\right)^2 \right] \right) }[/math] where [math]\displaystyle{ \rho }[/math] is the correlation between [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] and where [math]\displaystyle{ \sigma_X\gt 0 }[/math] and [math]\displaystyle{ \sigma_Y\gt 0 }[/math]. In this case,

[math]\displaystyle{ \boldsymbol\mu = \begin{pmatrix} \mu_X \\ \mu_Y \end{pmatrix}, \quad \boldsymbol\Sigma = \begin{pmatrix} \sigma_X^2 & \rho \sigma_X \sigma_Y \\ \rho \sigma_X \sigma_Y & \sigma_Y^2 \end{pmatrix}. }[/math]

In the bivariate case, the first equivalent condition for multivariate reconstruction of normality can be made less restrictive as it is sufficient to verify that a countably infinite set of distinct linear combinations of [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] are normal in order to conclude that the vector of [math]\displaystyle{ \text{[XY]′} }[/math] is bivariate normal.

The bivariate iso-density loci plotted in the [math]\displaystyle{ x,y }[/math]-plane are ellipses, whose principal axes are defined by the eigenvectors of the covariance matrix [math]\displaystyle{ \boldsymbol\Sigma }[/math] (the major and minor semidiameters of the ellipse equal the square-root of the ordered eigenvalues).

Bivariate normal distribution centered at [math]\displaystyle{ (1, 3) }[/math] with a standard deviation of 3 in roughly the [math]\displaystyle{ (0.878, 0.478) }[/math] direction and of 1 in the orthogonal direction.

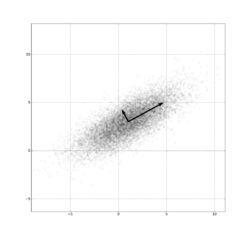
As the absolute value of the correlation parameter [math]\displaystyle{ \rho }[/math] increases, these loci are squeezed toward the following line :

[math]\displaystyle{ y(x) = \sgn (\rho)\frac{\sigma_Y}{\sigma_X} (x - \mu _X) + \mu_Y. }[/math]

This is because this expression, with [math]\displaystyle{ \sgn(\rho) }[/math] (where sgn is the Sign function) replaced by [math]\displaystyle{ \rho }[/math], is the best linear unbiased prediction of [math]\displaystyle{ Y }[/math] given a value of [math]\displaystyle{ X }[/math].

Degenerate case

If the covariance matrix [math]\displaystyle{ \boldsymbol\Sigma }[/math] is not full rank, then the multivariate normal distribution is degenerate and does not have a density. More precisely, it does not have a density with respect to k-dimensional Lebesgue measure (which is the usual measure assumed in calculus-level probability courses). Only random vectors whose distributions are absolutely continuous with respect to a measure are said to have densities (with respect to that measure). To talk about densities but avoid dealing with measure-theoretic complications it can be simpler to restrict attention to a subset of [math]\displaystyle{ \operatorname{rank}(\boldsymbol\Sigma) }[/math] of the coordinates of [math]\displaystyle{ \mathbf{x} }[/math] such that the covariance matrix for this subset is positive definite; then the other coordinates may be thought of as an affine function of these selected coordinates.

To talk about densities meaningfully in singular cases, then, we must select a different base measure. Using the disintegration theorem we can define a restriction of Lebesgue measure to the [math]\displaystyle{ \operatorname{rank}(\boldsymbol\Sigma) }[/math]-dimensional affine subspace of [math]\displaystyle{ \mathbb{R}^k }[/math] where the Gaussian distribution is supported, i.e. [math]\displaystyle{ \left\{\boldsymbol\mu + \boldsymbol{\Sigma^{1/2}}\mathbf{v} : \mathbf{v} \in \mathbb{R}^k\right\} }[/math]. With respect to this measure the distribution has the density of the following motif:

[math]\displaystyle{ f(\mathbf{x}) = \frac{e^{ -\frac{1}{2}\left(\mathbf{x} - \boldsymbol\mu\right)^\mathrm{T} \boldsymbol\Sigma^+\left(\mathbf{x} - \boldsymbol\mu\right) }}\sqrt{(2\pi)^k \det\nolimits^*(\boldsymbol\Sigma)} }[/math]

where [math]\displaystyle{ \boldsymbol\Sigma^+ }[/math] is the generalized inverse, [math]\displaystyle{ k }[/math] is the rank of [math]\displaystyle{ \boldsymbol\Sigma }[/math] and [math]\displaystyle{ \det\nolimits^* }[/math] is the pseudo-determinant.

Cumulative distribution function

The notion of cumulative distribution function (cdf) in dimension 1 can be extended in two ways to the multidimensional case, based on rectangular and ellipsoidal regions.

The first way is to define the cdf [math]\displaystyle{ F(\mathbf{x}) }[/math] of a random vector [math]\displaystyle{ \mathbf{X} }[/math] as the probability that all components of [math]\displaystyle{ \mathbf{X} }[/math] are less than or equal to the corresponding values in the vector [math]\displaystyle{ \mathbf{x} }[/math]:

[math]\displaystyle{ F(\mathbf{x}) = \mathbb{P}(\mathbf{X}\leq \mathbf{x}), \quad \text{where } \mathbf{X} \sim \mathcal{N}(\boldsymbol\mu,\, \boldsymbol\Sigma). }[/math]

Though there is no closed form for [math]\displaystyle{ F(\mathbf{x}) }[/math], there are a number of algorithms that estimate it numerically.

Another way is to define the cdf [math]\displaystyle{ F(r) }[/math] as the probability that a sample lies inside the ellipsoid determined by its Mahalanobis distance [math]\displaystyle{ r }[/math] from the Gaussian, a direct generalization of the standard deviation. In order to compute the values of this function, closed analytic formulae exist, as follows.

Interval

The interval for the multivariate normal distribution yields a region consisting of those vectors x satisfying

[math]\displaystyle{ ({\mathbf x}-{\boldsymbol\mu})^\mathrm{T}{\boldsymbol\Sigma}^{-1}({\mathbf x}-{\boldsymbol\mu}) \leq \chi^2_k(p). }[/math]

Here [math]\displaystyle{ {\mathbf x} }[/math] is a [math]\displaystyle{ k }[/math]-dimensional vector, [math]\displaystyle{ {\boldsymbol\mu} }[/math] is the known [math]\displaystyle{ k }[/math]-dimensional mean vector, [math]\displaystyle{ \boldsymbol\Sigma }[/math] is the known covariance matrix and [math]\displaystyle{ \chi^2_k(p) }[/math] is the quantile function for probability [math]\displaystyle{ p }[/math] of the chi-squared distribution with [math]\displaystyle{ k }[/math] degrees of freedom. When [math]\displaystyle{ k = 2, }[/math] the expression defines the interior of an ellipse and the chi-squared distribution simplifies to an exponential distribution with mean equal to two (rate equal to half).

Complementary cumulative distribution function (tail distribution)

The complementary cumulative distribution function (ccdf) or the tail distribution is defined as [math]\displaystyle{ \overline F(\mathbf{x}) = 1 - \mathbb P\left(\mathbf X\leq \mathbf x\right) }[/math]. When [math]\displaystyle{ \mathbf{X} \sim \mathcal{N}(\boldsymbol\mu,\, \boldsymbol\Sigma) }[/math], then the ccdf can be written as a probability the maximum of dependent Gaussian variables:

[math]\displaystyle{ \overline F(\mathbf{x}) = \mathbb P\left(\bigcup_i\{X_i\geq x_i\}\right) = \mathbb P\left(\max_i Y_i\geq 0\right), \quad \text{where } \mathbf{Y} \sim \mathcal{N}\left(\boldsymbol\mu - \mathbf{x},\, \boldsymbol\Sigma\right). }[/math]

While no simple closed formula exists for computing the ccdf, the maximum of dependent Gaussian variables can be estimated accurately via the Monte Carlo method.

Properties

Probability in different domains

Top: the probability of a bivariate normal in the domain [math]\displaystyle{ x\sin y-y\cos x\gt 1 }[/math] (blue regions). Middle: the probability of a trivariate normal in a toroidal domain. Bottom: converging Monte-Carlo integral of the probability of a 4-variate normal in the 4d regular polyhedral domain defined by [math]\displaystyle{ \sum_{i=1}^4 \vert x_i \vert \lt 1 }[/math]. These are all computed by the numerical method of ray-tracing.

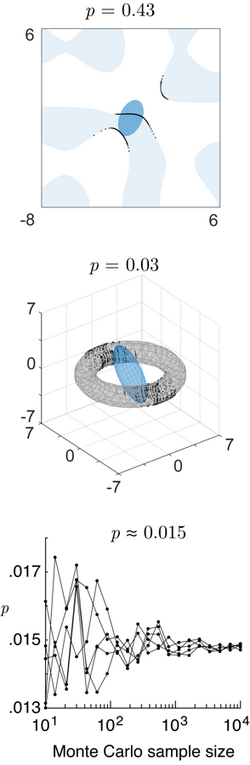
The probability content of the multivariate normal in a quadratic domain defined by [math]\displaystyle{ q(\boldsymbol{x}) = \boldsymbol{x}' \mathbf{Q_2} \boldsymbol{x} + \boldsymbol{q_1}' \boldsymbol{x} + q_0\gt 0 }[/math] (where [math]\displaystyle{ \mathbf{Q_2} }[/math] is a matrix, [math]\displaystyle{ \boldsymbol{q_1} }[/math] is a vector, and [math]\displaystyle{ q_0 }[/math] is a scalar), which is relevant for Bayesian classification/decision theory using Gaussian discriminant analysis, is given by the generalized chi-squared distribution. The probability content within any general domain defined by [math]\displaystyle{ f(\boldsymbol{x})\gt 0 }[/math] (where [math]\displaystyle{ f(\boldsymbol{x}) }[/math] is a general function) can be computed using the numerical method of ray-tracing (Matlab code).

Higher moments

The kth-order moments of x are given by

[math]\displaystyle{ \mu_{1,\ldots,N}(\mathbf{x}) \mathrel\stackrel{\mathrm{def}}{=} \mu _{r_1,\ldots,r_N}(\mathbf{x}) \mathrel\stackrel{\mathrm{def}}{=} \operatorname E\left[ \prod_{j=1}^N X_j^{r_j} \right] }[/math]

where r₁ + r₂ + ⋯ + r_N = k.

The kth-order central moments are as follows

1. If k is odd, μ_{1, …, N}(x − μ) = 0.
2. If k is even with k = 2λ, then [math]\displaystyle{ \mu_{1,\dots,2\lambda}(\mathbf{x}-\boldsymbol\mu ) = \sum \left( \sigma_{ij} \sigma_{k\ell} \cdots \sigma_{XZ}\right) }[/math]

where the sum is taken over all allocations of the set [math]\displaystyle{ \left\{ 1,\ldots,2\lambda \right\} }[/math] into λ (unordered) pairs. That is, for a kth (= 2λ = 6) central moment, one sums the products of λ = 3 covariances (the expected value μ is taken to be 0 in the interests of parsimony):

[math]\displaystyle{ \begin{align} & \operatorname E[X_1 X_2 X_3 X_4 X_5 X_6] \\[8pt] = {} & \operatorname E[X_1 X_2]\operatorname E[X_3 X_4]\operatorname E[X_5 X_6] + \operatorname E[X_1 X_2]\operatorname E[X_3 X_5]\operatorname E[X_4 X_6] + \operatorname E[X_1 X_2]\operatorname E[X_3 X_6] \operatorname E[X_4 X_5] \\[4pt] & {} + \operatorname E[X_1 X_3]\operatorname E[X_2 X_4]\operatorname E[X_5 X_6] + \operatorname E[X_1 X_3]\operatorname E[X_2 X_5]\operatorname E[X_4 X_6] + \operatorname E[X_1 X_3]\operatorname E[X_2 X_6] \operatorname E[X_4 X_5] \\[4pt] & {} + \operatorname E[X_1 X_4]\operatorname E[X_2 X_3]\operatorname E[X_5 X_6] + \operatorname E[X_1 X_4]\operatorname E[X_2 X_5]\operatorname E[X_3 X_6]+ \operatorname E[X_1 X_4]\operatorname E[X_2 X_6] \operatorname E[X_3 X_5] \\[4pt] & {} + \operatorname E[X_1 X_5]\operatorname E[X_2 X_3]\operatorname E[X_4 X_6] + \operatorname E[X_1 X_5]\operatorname E[X_2 X_4]\operatorname E[X_3 X_6] + \operatorname E[X_1 X_5]\operatorname E[X_2 X_6] \operatorname E[X_3 X_4] \\[4pt] & {} + \operatorname E[X_1 X_6]\operatorname E[X_2 X_3]\operatorname E[X_4 X_5] + \operatorname E[X_1 X_6]\operatorname E[X_2 X_4]\operatorname E[X_3 X_5] + \operatorname E[X_1 X_6] \operatorname E[X_2 X_5]\operatorname E[X_3 X_4]. \end{align} }[/math]

This yields [math]\displaystyle{ \tfrac{(2\lambda -1)!}{2^{\lambda -1}(\lambda -1)!} }[/math] terms in the sum (15 in the above case), each being the product of λ (in this case 3) covariances. For fourth order moments (four variables) there are three terms. For sixth-order moments there are 3 × 5 = 15 terms, and for eighth-order moments there are 3 × 5 × 7 = 105 terms.

The covariances are then determined by replacing the terms of the list [math]\displaystyle{ [ 1, \ldots, 2\lambda] }[/math] by the corresponding terms of the list consisting of r₁ ones, then r₂ twos, etc.. To illustrate this, examine the following 4th-order central moment case:

[math]\displaystyle{ \begin{align} \operatorname E \left [ X_i^4 \right ] & = 3\sigma_{ii}^2 \\[4pt] \operatorname E \left[ X_i^3 X_j \right ] & = 3\sigma_{ii} \sigma_{ij} \\[4pt] \operatorname E \left[ X_i^2 X_j^2 \right ] & = \sigma_{ii}\sigma_{jj}+2 \sigma _{ij}^2 \\[4pt] \operatorname E \left[ X_i^2 X_j X_k \right ] & = \sigma_{ii}\sigma _{jk}+2\sigma _{ij}\sigma_{ik} \\[4pt] \operatorname E \left [ X_i X_j X_k X_n \right ] & = \sigma_{ij}\sigma _{kn} + \sigma _{ik} \sigma_{jn} + \sigma_{in} \sigma _{jk}. \end{align} }[/math]

where [math]\displaystyle{ \sigma_{ij} }[/math] is the covariance of X_i and X_j. With the above method one first finds the general case for a kth moment with k different X variables, [math]\displaystyle{ E\left[ X_i X_j X_k X_n\right] }[/math], and then one simplifies this accordingly. For example, for [math]\displaystyle{ \operatorname E[ X_i^2 X_k X_n ] }[/math], one lets X_i = X_j and one uses the fact that [math]\displaystyle{ \sigma_{ii} = \sigma_i^2 }[/math].

Functions of a normal vector

a: Probability density of a function [math]\displaystyle{ \cos x^2 }[/math] of a single normal variable [math]\displaystyle{ x }[/math] with [math]\displaystyle{ \mu=-2 }[/math] and [math]\displaystyle{ \sigma=3 }[/math]. b: Probability density of a function [math]\displaystyle{ x^y }[/math] of a normal vector [math]\displaystyle{ (x, y) }[/math], with mean [math]\displaystyle{ \boldsymbol{\mu}=(1, 2) }[/math], and covariance [math]\displaystyle{ \mathbf{\Sigma} = \begin{bmatrix} .01 & .016 \\ .016 & .04 \end{bmatrix} }[/math]. c: Heat map of the joint probability density of two functions of a normal vector [math]\displaystyle{ (x, y) }[/math], with mean [math]\displaystyle{ \boldsymbol{\mu}=(-2, 5) }[/math], and covariance [math]\displaystyle{ \mathbf{\Sigma} = \begin{bmatrix} 10 & -7 \\ -7 & 10 \end{bmatrix} }[/math]. d: Probability density of a function [math]\displaystyle{ \sum_{i=1}^4 \vert x_i \vert }[/math] of 4 iid standard normal variables. These are computed by the numerical method of ray-tracing.

A quadratic form of a normal vector [math]\displaystyle{ \boldsymbol{x} }[/math], [math]\displaystyle{ q(\boldsymbol{x}) = \boldsymbol{x}' \mathbf{Q_2} \boldsymbol{x} + \boldsymbol{q_1}' \boldsymbol{x} + q_0 }[/math] (where [math]\displaystyle{ \mathbf{Q_2} }[/math] is a matrix, [math]\displaystyle{ \boldsymbol{q_1} }[/math] is a vector, and [math]\displaystyle{ q_0 }[/math] is a scalar), is a generalized chi-squared variable. The direction of a normal vector follows a projected normal distribution.

If [math]\displaystyle{ f(\boldsymbol{x}) }[/math] is a general scalar-valued function of a normal vector, its probability density function, cumulative distribution function, and inverse cumulative distribution function can be computed with the numerical method of ray-tracing (Matlab code).

Likelihood function

If the mean and covariance matrix are known, the log likelihood of an observed vector [math]\displaystyle{ \boldsymbol{x} }[/math] is simply the log of the probability density function:

[math]\displaystyle{ \ln L (\boldsymbol{x})= -\frac{1}{2} \left[ \ln (|\boldsymbol\Sigma|\,) + (\boldsymbol{x}-\boldsymbol\mu)'\boldsymbol\Sigma^{-1}(\boldsymbol{x}-\boldsymbol\mu) + k\ln(2\pi) \right] }[/math],

The circularly symmetric version of the noncentral complex case, where [math]\displaystyle{ \boldsymbol{z} }[/math] is a vector of complex numbers, would be

[math]\displaystyle{ \ln L (\boldsymbol{z}) = -\ln (|\boldsymbol\Sigma|\,) -(\boldsymbol{z}-\boldsymbol\mu)^\dagger\boldsymbol\Sigma^{-1}(\boldsymbol{z}-\boldsymbol\mu) -k\ln(\pi) }[/math]

i.e. with the conjugate transpose (indicated by [math]\displaystyle{ \dagger }[/math]) replacing the normal transpose (indicated by [math]\displaystyle{ ' }[/math]). This is slightly different than in the real case, because the circularly symmetric version of the complex normal distribution has a slightly different form for the normalization constant.

A similar notation is used for multiple linear regression.

Since the log likelihood of a normal vector is a quadratic form of the normal vector, it is distributed as a generalized chi-squared variable.

Differential entropy

The differential entropy of the multivariate normal distribution is

[math]\displaystyle{ \begin{align} h\left(f\right) & = -\int_{-\infty}^\infty \int_{-\infty}^\infty \cdots\int_{-\infty}^\infty f(\mathbf{x}) \ln f(\mathbf{x})\,d\mathbf{x}\\ & = \frac12 \ln{} \left|2\pi e\boldsymbol\Sigma \right| = \frac{k}{2} + \frac{k}{2} \ln{} 2\pi + \frac{1}{2} \ln{} \left|\boldsymbol\Sigma \right|\\ \end{align} }[/math]

where the bars denote the matrix determinant, k is the dimensionality of the vector space, and the result has units of nats.

Kullback–Leibler divergence

The Kullback–Leibler divergence from [math]\displaystyle{ \mathcal{N}_1(\boldsymbol\mu_1, \boldsymbol\Sigma_1) }[/math] to [math]\displaystyle{ \mathcal{N}_0(\boldsymbol\mu_0, \boldsymbol\Sigma_0) }[/math], for non-singular matrices Σ₁ and Σ₀, is:

[math]\displaystyle{ D_\text{KL}(\mathcal{N}_0 \parallel \mathcal{N}_1) = { 1 \over 2 } \left\{ \operatorname{tr} \left( \boldsymbol\Sigma_1^{-1} \boldsymbol\Sigma_0 \right) + \left( \boldsymbol\mu_1 - \boldsymbol\mu_0\right)^{\rm T} \boldsymbol\Sigma_1^{-1} ( \boldsymbol\mu_1 - \boldsymbol\mu_0 ) - k +\ln { | \boldsymbol \Sigma_1 | \over | \boldsymbol\Sigma_0 | } \right\}, }[/math]

where [math]\displaystyle{ |\cdot| }[/math] denotes the matrix determinant, [math]\displaystyle{ tr(\cdot) }[/math] is the trace, [math]\displaystyle{ ln(\cdot) }[/math] is the natural logarithm and [math]\displaystyle{ k }[/math] is the dimension of the vector space.

The logarithm must be taken to base e since the two terms following the logarithm are themselves base-e logarithms of expressions that are either factors of the density function or otherwise arise naturally. The equation therefore gives a result measured in nats. Dividing the entire expression above by log_e 2 yields the divergence in bits.

When [math]\displaystyle{ \boldsymbol\mu_1 = \boldsymbol\mu_0 }[/math],

[math]\displaystyle{ D_\text{KL}(\mathcal{N}_0 \parallel \mathcal{N}_1) = { 1 \over 2 } \left\{ \operatorname{tr} \left( \boldsymbol\Sigma_1^{-1} \boldsymbol\Sigma_0 \right) - k +\ln { | \boldsymbol \Sigma_1 | \over | \boldsymbol\Sigma_0 | }\right\}. }[/math]

Mutual information

The mutual information of a distribution is a special case of the Kullback–Leibler divergence in which [math]\displaystyle{ P }[/math] is the full multivariate distribution and [math]\displaystyle{ Q }[/math] is the product of the 1-dimensional marginal distributions. In the notation of the Kullback–Leibler divergence section of this article, [math]\displaystyle{ \boldsymbol\Sigma_1 }[/math] is a diagonal matrix with the diagonal entries of [math]\displaystyle{ \boldsymbol\Sigma_0 }[/math], and [math]\displaystyle{ \boldsymbol\mu_1 = \boldsymbol\mu_0 }[/math]. The resulting formula for mutual information is:

[math]\displaystyle{ I(\boldsymbol{X}) = - { 1 \over 2 } \ln | \boldsymbol \rho_0 |, }[/math]

where [math]\displaystyle{ \boldsymbol \rho_0 }[/math] is the correlation matrix constructed from [math]\displaystyle{ \boldsymbol \Sigma_0 }[/math].

In the bivariate case the expression for the mutual information is:

[math]\displaystyle{ I(x;y) = - { 1 \over 2 } \ln (1 - \rho^2). }[/math]

Joint normality

Normally distributed and independent

If [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] are normally distributed and independent, this implies they are "jointly normally distributed", i.e., the pair [math]\displaystyle{ (X,Y) }[/math] must have multivariate normal distribution. However, a pair of jointly normally distributed variables need not be independent (would only be so if uncorrelated, [math]\displaystyle{ \rho = 0 }[/math] ).

Two normally distributed random variables need not be jointly bivariate normal

The fact that two random variables [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] both have a normal distribution does not imply that the pair [math]\displaystyle{ (X,Y) }[/math] has a joint normal distribution. A simple example is one in which X has a normal distribution with expected value 0 and variance 1, and [math]\displaystyle{ Y=X }[/math] if [math]\displaystyle{ |X| \gt c }[/math] and [math]\displaystyle{ Y=-X }[/math] if [math]\displaystyle{ |X| \lt c }[/math], where [math]\displaystyle{ c \gt 0 }[/math]. There are similar counterexamples for more than two random variables. In general, they sum to a mixture model.

Correlations and independence

In general, random variables may be uncorrelated but statistically dependent. But if a random vector has a multivariate normal distribution then any two or more of its components that are uncorrelated are independent. This implies that any two or more of its components that are pairwise independent are independent. But, as pointed out just above, it is not true that two random variables that are (separately, marginally) normally distributed and uncorrelated are independent.

Conditional distributions

If N-dimensional x is partitioned as follows

[math]\displaystyle{ \mathbf{x} = \begin{bmatrix} \mathbf{x}_1 \\ \mathbf{x}_2 \end{bmatrix} \text{ with sizes }\begin{bmatrix} q \times 1 \\ (N-q) \times 1 \end{bmatrix} }[/math]

and accordingly μ and Σ are partitioned as follows

[math]\displaystyle{ \boldsymbol\mu = \begin{bmatrix} \boldsymbol\mu_1 \\ \boldsymbol\mu_2 \end{bmatrix} \text{ with sizes }\begin{bmatrix} q \times 1 \\ (N-q) \times 1 \end{bmatrix} }[/math]

[math]\displaystyle{ \boldsymbol\Sigma = \begin{bmatrix} \boldsymbol\Sigma_{11} & \boldsymbol\Sigma_{12} \\ \boldsymbol\Sigma_{21} & \boldsymbol\Sigma_{22} \end{bmatrix} \text{ with sizes }\begin{bmatrix} q \times q & q \times (N-q) \\ (N-q) \times q & (N-q) \times (N-q) \end{bmatrix} }[/math]

then the distribution of x₁ conditional on x₂ = a is multivariate normal (x₁ | x₂ = a) ~ N(μ, Σ) where

[math]\displaystyle{ \bar{\boldsymbol\mu} = \boldsymbol\mu_1 + \boldsymbol\Sigma_{12} \boldsymbol\Sigma_{22}^{-1} \left( \mathbf{a} - \boldsymbol\mu_2 \right) }[/math]

and covariance matrix

[math]\displaystyle{ \overline{\boldsymbol\Sigma} = \boldsymbol\Sigma_{11} - \boldsymbol\Sigma_{12} \boldsymbol\Sigma_{22}^{-1} \boldsymbol\Sigma_{21}. }[/math]

Here [math]\displaystyle{ \boldsymbol\Sigma_{22}^{-1} }[/math] is the generalized inverse of [math]\displaystyle{ \boldsymbol\Sigma_{22} }[/math]. The matrix [math]\displaystyle{ \overline{\boldsymbol\Sigma} }[/math] is the Schur complement of Σ₂₂ in Σ. That is, the equation above is equivalent to inverting the overall covariance matrix, dropping the rows and columns corresponding to the variables being conditioned upon, and inverting back to get the conditional covariance matrix.

Note that knowing that x₂ = a alters the variance, though the new variance does not depend on the specific value of a; perhaps more surprisingly, the mean is shifted by [math]\displaystyle{ \boldsymbol\Sigma_{12} \boldsymbol\Sigma_{22}^{-1} \left(\mathbf{a} - \boldsymbol\mu_2 \right) }[/math]; compare this with the situation of not knowing the value of a, in which case x₁ would have distribution [math]\displaystyle{ \mathcal{N}_q \left(\boldsymbol\mu_1, \boldsymbol\Sigma_{11} \right) }[/math].

An interesting fact derived in order to prove this result, is that the random vectors [math]\displaystyle{ \mathbf{x}_2 }[/math] and [math]\displaystyle{ \mathbf{y}_1=\mathbf{x}_1-\boldsymbol\Sigma_{12}\boldsymbol\Sigma_{22}^{-1}\mathbf{x}_2 }[/math] are independent.

The matrix Σ₁₂Σ₂₂⁻¹ is known as the matrix of regression coefficients.

Bivariate case

In the bivariate case where x is partitioned into [math]\displaystyle{ X_1 }[/math] and [math]\displaystyle{ X_2 }[/math], the conditional distribution of [math]\displaystyle{ X_1 }[/math] given [math]\displaystyle{ X_2 }[/math] is

[math]\displaystyle{ X_1\mid X_2=a \ \sim\ \mathcal{N}\left(\mu_1+\frac{\sigma_1}{\sigma_2}\rho( a - \mu_2),\, (1-\rho^2)\sigma_1^2\right) }[/math]

where [math]\displaystyle{ \rho }[/math] is the correlation coefficient between [math]\displaystyle{ X_1 }[/math] and [math]\displaystyle{ X_2 }[/math].

Bivariate conditional expectation

In the general case

[math]\displaystyle{ \begin{pmatrix} X_1 \\ X_2 \end{pmatrix} \sim \mathcal{N} \left( \begin{pmatrix} \mu_1 \\ \mu_2 \end{pmatrix} , \begin{pmatrix} \sigma^2_1 & \rho \sigma_1 \sigma_2 \\ \rho \sigma_1 \sigma_2 & \sigma^2_2 \end{pmatrix} \right) }[/math]

The conditional expectation of X₁ given X₂ is:

[math]\displaystyle{ \operatorname{E}(X_1 \mid X_2=x_2) = \mu_1 + \rho \frac{\sigma_1}{\sigma_2}(x_2 - \mu_2) }[/math]

Proof: the result is obtained by taking the expectation of the conditional distribution [math]\displaystyle{ X_1\mid X_2 }[/math] above.

In the centered case with unit variances

[math]\displaystyle{ \begin{pmatrix} X_1 \\ X_2 \end{pmatrix} \sim \mathcal{N} \left( \begin{pmatrix} 0 \\ 0 \end{pmatrix} , \begin{pmatrix} 1 & \rho \\ \rho & 1 \end{pmatrix} \right) }[/math]

The conditional expectation of X₁ given X₂ is

[math]\displaystyle{ \operatorname{E}(X_1 \mid X_2=x_2)= \rho x_2 }[/math]

and the conditional variance is

[math]\displaystyle{ \operatorname{var}(X_1 \mid X_2 = x_2) = 1-\rho^2; }[/math]

thus the conditional variance does not depend on x₂.

The conditional expectation of X₁ given that X₂ is smaller/bigger than z is:

[math]\displaystyle{ \operatorname{E}(X_1 \mid X_2 \lt z) = -\rho { \varphi(z) \over \Phi(z) } , }[/math]

[math]\displaystyle{ \operatorname{E}(X_1 \mid X_2 \gt z) = \rho { \varphi(z) \over (1- \Phi(z)) } , }[/math]

where the final ratio here is called the inverse Mills ratio.

Proof: the last two results are obtained using the result [math]\displaystyle{ \operatorname{E}(X_1 \mid X_2=x_2)= \rho x_2 }[/math], so that

[math]\displaystyle{ \operatorname{E}(X_1 \mid X_2 \lt z) = \rho E(X_2 \mid X_2 \lt z) }[/math] and then using the properties of the expectation of a truncated normal distribution.

Marginal distributions

To obtain the marginal distribution over a subset of multivariate normal random variables, one only needs to drop the irrelevant variables (the variables that one wants to marginalize out) from the mean vector and the covariance matrix. The proof for this follows from the definitions of multivariate normal distributions and linear algebra.

Example

Let X = [X₁, X₂, X₃] be multivariate normal random variables with mean vector μ = [μ₁, μ₂, μ₃] and covariance matrix Σ (standard parametrization for multivariate normal distributions). Then the joint distribution of X′ = [X₁, X₃] is multivariate normal with mean vector μ′ = [μ₁, μ₃] and covariance matrix [math]\displaystyle{ \boldsymbol\Sigma' = \begin{bmatrix} \boldsymbol\Sigma_{11} & \boldsymbol\Sigma_{13} \\ \boldsymbol\Sigma_{31} & \boldsymbol\Sigma_{33} \end{bmatrix} }[/math].

Affine transformation

If Y = c + BX is an affine transformation of [math]\displaystyle{ \mathbf{X}\ \sim \mathcal{N}(\boldsymbol\mu, \boldsymbol\Sigma), }[/math] where c is an [math]\displaystyle{ M \times 1 }[/math] vector of constants and B is a constant [math]\displaystyle{ M \times N }[/math] matrix, then Y has a multivariate normal distribution with expected value c + Bμ and variance BΣB^T i.e., [math]\displaystyle{ \mathbf{Y} \sim \mathcal{N} \left(\mathbf{c} + \mathbf{B} \boldsymbol\mu, \mathbf{B} \boldsymbol\Sigma \mathbf{B}^{\rm T}\right) }[/math]. In particular, any subset of the X_i has a marginal distribution that is also multivariate normal. To see this, consider the following example: to extract the subset (X₁, X₂, X₄)^T, use

[math]\displaystyle{ \mathbf{B} = \begin{bmatrix} 1 & 0 & 0 & 0 & 0 & \ldots & 0 \\ 0 & 1 & 0 & 0 & 0 & \ldots & 0 \\ 0 & 0 & 0 & 1 & 0 & \ldots & 0 \end{bmatrix} }[/math]

which extracts the desired elements directly.

Another corollary is that the distribution of Z = b · X, where b is a constant vector with the same number of elements as X and the dot indicates the dot product, is univariate Gaussian with [math]\displaystyle{ Z\sim\mathcal{N}\left(\mathbf{b}\cdot\boldsymbol\mu, \mathbf{b}^{\rm T}\boldsymbol\Sigma \mathbf{b}\right) }[/math]. This result follows by using

[math]\displaystyle{ \mathbf{B}=\begin{bmatrix} b_1 & b_2 & \ldots & b_n \end{bmatrix} = \mathbf{b}^{\rm T}. }[/math]

Observe how the positive-definiteness of Σ implies that the variance of the dot product must be positive.

An affine transformation of X such as 2X is not the same as the sum of two independent realisations of X.

Geometric interpretation

The equidensity contours of a non-singular multivariate normal distribution are ellipsoids (i.e. affine transformations of hyperspheres) centered at the mean. Hence the multivariate normal distribution is an example of the class of elliptical distributions. The directions of the principal axes of the ellipsoids are given by the eigenvectors of the covariance matrix [math]\displaystyle{ \boldsymbol\Sigma }[/math]. The squared relative lengths of the principal axes are given by the corresponding eigenvalues.

If Σ = UΛU^T = UΛ^1/2(UΛ^1/2)^T is an eigendecomposition where the columns of U are unit eigenvectors and Λ is a diagonal matrix of the eigenvalues, then we have

[math]\displaystyle{ \mathbf{X}\ \sim \mathcal{N}(\boldsymbol\mu, \boldsymbol\Sigma) \iff \mathbf{X}\ \sim \boldsymbol\mu+\mathbf{U}\boldsymbol\Lambda^{1/2}\mathcal{N}(0, \mathbf{I}) \iff \mathbf{X}\ \sim \boldsymbol\mu+\mathbf{U}\mathcal{N}(0, \boldsymbol\Lambda). }[/math]

Moreover, U can be chosen to be a rotation matrix, as inverting an axis does not have any effect on N(0, Λ), but inverting a column changes the sign of U's determinant. The distribution N(μ, Σ) is in effect N(0, I) scaled by Λ^1/2, rotated by U and translated by μ.

Conversely, any choice of μ, full rank matrix U, and positive diagonal entries Λ_i yields a non-singular multivariate normal distribution. If any Λ_i is zero and U is square, the resulting covariance matrix UΛU^T is singular. Geometrically this means that every contour ellipsoid is infinitely thin and has zero volume in n-dimensional space, as at least one of the principal axes has length of zero; this is the degenerate case.

"The radius around the true mean in a bivariate normal random variable, re-written in polar coordinates (radius and angle), follows a Hoyt distribution."

In one dimension the probability of finding a sample of the normal distribution in the interval [math]\displaystyle{ \mu\pm \sigma }[/math] is approximately 68.27%, but in higher dimensions the probability of finding a sample in the region of the standard deviation ellipse is lower.

Dimensionality	Probability
1	0.6827
2	0.3935
3	0.1987
4	0.0902
5	0.0374
6	0.0144
7	0.0052
8	0.0018
9	0.0006
10	0.0002

Statistical inference

Parameter estimation

Further information: Estimation of covariance matrices

The derivation of the maximum-likelihood estimator of the covariance matrix of a multivariate normal distribution is straightforward.

In short, the probability density function (pdf) of a multivariate normal is

[math]\displaystyle{ f(\mathbf{x})= \frac{1}{\sqrt { (2\pi)^k|\boldsymbol \Sigma| } } \exp\left(-{1 \over 2} (\mathbf{x}-\boldsymbol\mu)^{\rm T} \boldsymbol\Sigma^{-1} ({\mathbf x}-\boldsymbol\mu)\right) }[/math]

and the ML estimator of the covariance matrix from a sample of n observations is

[math]\displaystyle{ \widehat{\boldsymbol\Sigma} = {1 \over n}\sum_{i=1}^n ({\mathbf x}_i-\overline{\mathbf x})({\mathbf x}_i-\overline{\mathbf x})^\mathrm{T} }[/math]

which is simply the sample covariance matrix. This is a biased estimator whose expectation is

[math]\displaystyle{ E\left[\widehat{\boldsymbol\Sigma}\right] = \frac{n-1}{n} \boldsymbol\Sigma. }[/math]

An unbiased sample covariance is

[math]\displaystyle{ \widehat{\boldsymbol\Sigma} = \frac1{n-1}\sum_{i=1}^n (\mathbf{x}_i-\overline{\mathbf{x}})(\mathbf{x}_i-\overline{\mathbf{x}})^{\rm T} = \frac1{n-1} \left[X'\left(I - \frac{1}{n} \cdot J\right) X\right] }[/math] (matrix form; [math]\displaystyle{ I }[/math] is the [math]\displaystyle{ K\times K }[/math] identity matrix, J is a [math]\displaystyle{ K \times K }[/math] matrix of ones; the term in parentheses is thus the [math]\displaystyle{ K \times K }[/math] centering matrix)

The Fisher information matrix for estimating the parameters of a multivariate normal distribution has a closed form expression. This can be used, for example, to compute the Cramér–Rao bound for parameter estimation in this setting. See Fisher information for more details.

Bayesian inference

In Bayesian statistics, the conjugate prior of the mean vector is another multivariate normal distribution, and the conjugate prior of the covariance matrix is an inverse-Wishart distribution [math]\displaystyle{ \mathcal{W}^{-1} }[/math] . Suppose then that n observations have been made

[math]\displaystyle{ \mathbf{X} = \{\mathbf{x}_1,\dots,\mathbf{x}_n\} \sim \mathcal{N}(\boldsymbol\mu,\boldsymbol\Sigma) }[/math]

and that a conjugate prior has been assigned, where

[math]\displaystyle{ p(\boldsymbol\mu,\boldsymbol\Sigma)=p(\boldsymbol\mu\mid\boldsymbol\Sigma)\ p(\boldsymbol\Sigma), }[/math]

where

[math]\displaystyle{ p(\boldsymbol\mu\mid\boldsymbol\Sigma) \sim\mathcal{N}(\boldsymbol\mu_0,m^{-1}\boldsymbol\Sigma) , }[/math]

and

[math]\displaystyle{ p(\boldsymbol\Sigma) \sim \mathcal{W}^{-1}(\boldsymbol\Psi,n_0). }[/math]

Then

[math]\displaystyle{ \begin{array}{rcl} p(\boldsymbol\mu\mid\boldsymbol\Sigma,\mathbf{X}) & \sim & \mathcal{N}\left(\frac{n\bar{\mathbf{x}} + m\boldsymbol\mu_0}{n+m},\frac{1}{n+m}\boldsymbol\Sigma\right),\\ p(\boldsymbol\Sigma\mid\mathbf{X}) & \sim & \mathcal{W}^{-1}\left(\boldsymbol\Psi+n\mathbf{S}+\frac{nm}{n+m}(\bar{\mathbf{x}}-\boldsymbol\mu_0)(\bar{\mathbf{x}}-\boldsymbol\mu_0)', n+n_0\right), \end{array} }[/math]

where

[math]\displaystyle{ \begin{align} \bar{\mathbf{x}} & = \frac{1}{n}\sum_{i=1}^{n} \mathbf{x}_i ,\\ \mathbf{S} & = \frac{1}{n}\sum_{i=1}^{n} (\mathbf{x}_i - \bar{\mathbf{x}})(\mathbf{x}_i - \bar{\mathbf{x}})' . \end{align} }[/math]

Multivariate normality tests

Multivariate normality tests check a given set of data for similarity to the multivariate normal distribution. The null hypothesis is that the data set is similar to the normal distribution, therefore a sufficiently small p-value indicates non-normal data. Multivariate normality tests include the Cox–Small test and Smith and Jain's adaptation of the Friedman–Rafsky test created by Larry Rafsky and Jerome Friedman.

Mardia's test is based on multivariate extensions of skewness and kurtosis measures. For a sample {x₁, ..., x_n} of k-dimensional vectors we compute

[math]\displaystyle{ \begin{align} & \widehat{\boldsymbol\Sigma} = {1 \over n} \sum_{j=1}^n \left(\mathbf{x}_j - \bar{\mathbf{x}}\right)\left(\mathbf{x}_j - \bar{\mathbf{x}}\right)^\mathrm{T} \\ & A = {1 \over 6n} \sum_{i=1}^n \sum_{j=1}^n \left[ (\mathbf{x}_i - \bar{\mathbf{x}})^\mathrm{T}\;\widehat{\boldsymbol\Sigma}^{-1} (\mathbf{x}_j - \bar{\mathbf{x}}) \right]^3 \\ & B = \sqrt{\frac{n}{8k(k+2)}}\left\{{1 \over n} \sum_{i=1}^n \left[ (\mathbf{x}_i - \bar{\mathbf{x}})^\mathrm{T}\;\widehat{\boldsymbol\Sigma}^{-1} (\mathbf{x}_i - \bar{\mathbf{x}}) \right]^2 - k(k+2) \right\} \end{align} }[/math]

Under the null hypothesis of multivariate normality, the statistic A will have approximately a chi-squared distribution with 1/6⋅k(k + 1)(k + 2) degrees of freedom, and B will be approximately standard normal N(0,1).

Mardia's kurtosis statistic is skewed and converges very slowly to the limiting normal distribution. For medium size samples [math]\displaystyle{ (50 \le n \lt 400) }[/math], the parameters of the asymptotic distribution of the kurtosis statistic are modified For small sample tests ([math]\displaystyle{ n\lt 50 }[/math]) empirical critical values are used. Tables of critical values for both statistics are given by Rencher for k = 2, 3, 4.

Mardia's tests are affine invariant but not consistent. For example, the multivariate skewness test is not consistent against symmetric non-normal alternatives.

The BHEP test computes the norm of the difference between the empirical characteristic function and the theoretical characteristic function of the normal distribution. Calculation of the norm is performed in the L²(μ) space of square-integrable functions with respect to the Gaussian weighting function [math]\displaystyle{ \mu_\beta(\mathbf{t}) = (2\pi\beta^2)^{-k/2} e^{-|\mathbf{t}|^2/(2\beta^2)} }[/math]. The test statistic is

[math]\displaystyle{ \begin{align} T_\beta &= \int_{\mathbb{R}^k} \left| {1 \over n} \sum_{j=1}^n e^{i\mathbf{t}^\mathrm{T}\widehat{\boldsymbol\Sigma}^{-1/2}(\mathbf{x}_j - \bar{\mathbf{x})}} - e^{-|\mathbf{t}|^2/2} \right|^2 \; \boldsymbol\mu_\beta(\mathbf{t}) \, d\mathbf{t} \\ &= {1 \over n^2} \sum_{i,j=1}^n e^{-{\beta^2 \over 2}(\mathbf{x}_i-\mathbf{x}_j)^\mathrm{T}\widehat{\boldsymbol\Sigma}^{-1}(\mathbf{x}_i-\mathbf{x}_j)} - \frac{2}{n(1 + \beta^2)^{k/2}}\sum_{i=1}^n e^{ -\frac{\beta^2}{2(1+\beta^2)} (\mathbf{x}_i-\bar{\mathbf{x}})^\mathrm{T}\widehat{\boldsymbol\Sigma}^{-1}(\mathbf{x}_i-\bar{\mathbf{x}})} + \frac{1}{(1 + 2\beta^2)^{k/2}} \end{align} }[/math]

The limiting distribution of this test statistic is a weighted sum of chi-squared random variables.

A detailed survey of these and other test procedures is available.

Classification into multivariate normal classes

Left: Classification of seven multivariate normal classes. Coloured ellipses are 1 sd error ellipses. Black marks the boundaries between the classification regions. [math]\displaystyle{ p_e }[/math] is the probability of total classification error. Right: the error matrix. [math]\displaystyle{ p_{ij} }[/math] is the probability of classifying a sample from normal [math]\displaystyle{ i }[/math] as [math]\displaystyle{ j }[/math]. These are computed by the numerical method of ray-tracing (Matlab code).

Gaussian Discriminant Analysis

Suppose that observations (which are vectors) are presumed to come from one of several multivariate normal distributions, with known means and covariances. Then any given observation can be assigned to the distribution from which it has the highest probability of arising. This classification procedure is called Gaussian discriminant analysis. The classification performance, i.e. probabilities of the different classification outcomes, and the overall classification error, can be computed by the numerical method of ray-tracing (Matlab code).

Computational methods

Drawing values from the distribution

A widely used method for drawing (sampling) a random vector x from the N-dimensional multivariate normal distribution with mean vector μ and covariance matrix Σ works as follows:

1. Find any real matrix A such that A A^T = Σ. When Σ is positive-definite, the Cholesky decomposition is typically used, and the extended form of this decomposition can always be used (as the covariance matrix may be only positive semi-definite) in both cases a suitable matrix A is obtained. An alternative is to use the matrix A = UΛ^½ obtained from a spectral decomposition Σ = UΛU⁻¹ of Σ. The former approach is more computationally straightforward but the matrices A change for different orderings of the elements of the random vector, while the latter approach gives matrices that are related by simple re-orderings. In theory both approaches give equally good ways of determining a suitable matrix A, but there are differences in computation time.
2. Let z = (z₁, …, z_N)^T be a vector whose components are N independent standard normal variates (which can be generated, for example, by using the Box–Muller transform).
3. Let x be μ + Az. This has the desired distribution due to the affine transformation property.

See also

• Chi distribution, the pdf of the 2-norm (Euclidean norm or vector length) of a multivariate normally distributed vector (uncorrelated and zero centered).
  • Rayleigh distribution, the pdf of the vector length of a bivariate normally distributed vector (uncorrelated and zero centered)
  • Rice distribution, the pdf of the vector length of a bivariate normally distributed vector (uncorrelated and non-centered)
  • Hoyt distribution, the pdf of the vector length of a bivariate normally distributed vector (correlated and centered)
• Complex normal distribution, an application of bivariate normal distribution
• Copula, for the definition of the Gaussian or normal copula model.
• Multivariate t-distribution, which is another widely used spherically symmetric multivariate distribution.
• Multivariate stable distribution extension of the multivariate normal distribution, when the index (exponent in the characteristic function) is between zero and two.
• Mahalanobis distance
• Wishart distribution
• Matrix normal distribution

References

Literature

• Rencher, A.C. (1995). Methods of Multivariate Analysis. New York: Wiley. 
• Tong, Y. L. (1990). The multivariate normal distribution. Springer Series in Statistics. New York: Springer-Verlag. doi:10.1007/978-1-4613-9655-0. ISBN 978-1-4613-9657-4.