Gaussian correlation inequality
The Gaussian correlation inequality (GCI), formerly known as the Gaussian correlation conjecture (GCC), is a mathematical theorem in the fields of mathematical statistics and convex geometry.
The statement
The Gaussian correlation inequality states:
Let [math]\displaystyle{ \mu }[/math] be an n-dimensional Gaussian probability measure on [math]\displaystyle{ \mathbb{R}^n }[/math], i.e. [math]\displaystyle{ \mu }[/math] a multivariate normal distribution, centered at the origin. Then for all convex sets [math]\displaystyle{ E,F \subset \mathbb{R}^n }[/math] that are symmetric about the origin,
- [math]\displaystyle{ \mu(E \cap F) \geq \mu(E) \cdot \mu(F). }[/math]
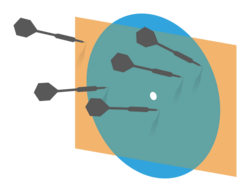
As a simple example for n=2, one can think of darts being thrown at a board, with their landing spots in the plane distributed according to a 2-variable normal distribution centered at the origin. (This is a reasonable assumption for any given darts player, with different players being described by different normal distributions.) If we now consider a circle and a rectangle in the plane, both centered at the origin, then the proportion of the darts landing in the intersection of both shapes is no less than the product of the proportions of the darts landing in each shape. This can also be formulated in terms of conditional probabilities: if you're informed that your last dart hit the rectangle, then this information will increase your estimate of the probability that the dart hit the circle.
History
A special case of the inequality was conjectured in 1955;[1] further development was given by Olive Jean Dunn in 1958.[2][3] The general case was stated in 1972, also as a conjecture.[4] The case of dimension n=2 was proved in 1977[5] and certain special cases of higher dimension have also been proven in subsequent years.[6]
The general case of the inequality remained open until 2014, when Thomas Royen, a retired German statistician, proved it using relatively elementary tools.[7] In fact, Royen generalized the conjecture and proved it for multivariate gamma distributions. The proof did not gain attention when it was published in 2014, due to Royen's relative anonymity and the fact that the proof was published in a predatory journal.[2][8] Another reason was a history of false proofs (by others) and many failed attempts to prove the conjecture, causing skepticism among mathematicians in the field.[2]
The conjecture, and its solution, came to public attention in 2017, when other mathematicians described Royen's proof in a mainstream publication[9] and popular media reported on the story.[2][10][11]
References
- ↑ Dunnett, C. W.; Sobel, M. (1955). "Approximations to the probability integral and certain percentage points of a multivariate analogue of Student's t -distribution" (in en). Biometrika 42 (1–2): 258–267. doi:10.1093/biomet/42.1-2.258. ISSN 0006-3444.
- ↑ 2.0 2.1 2.2 2.3 Wolchover, Natalie (March 28, 2017). "A Long-Sought Proof, Found and Almost Lost". QUANTA magazine. https://www.quantamagazine.org/statistician-proves-gaussian-correlation-inequality-20170328/.
- ↑ Schechtman, G.; Schlumprecht, Th.; Zinn, J. (January 1998). "On the Gaussian measure of the intersection". The Annals of Probability 26 (1): 346–357. doi:10.1214/aop/1022855422. ISSN 0091-1798.
- ↑ Das Gupta, S.; Eaton, M. L.; Olkin, I.; Perlman, M.; Savage, L. J.; Sobel, M. (1972). "Inequalities on the probability content of convex regions for elliptically contoured distributions". Proceedings of the Sixth Berkeley Symposium on Mathematical Statistics and Probability. II: Probability theory. Berkeley, California: Univ. California Press. pp. 241–265.
- ↑ Pitt, Loren D. (1977). "A Gaussian Correlation Inequality for Symmetric Convex Sets". The Annals of Probability 5 (3): 470–474. doi:10.1214/aop/1176995808. https://projecteuclid.org/journals/annals-of-probability/volume-5/issue-3/A-Gaussian-Correlation-Inequality-for-Symmetric-Convex-Sets/10.1214/aop/1176995808.full.
- ↑ Harge, Gilles (1999). "A Particular Case of Correlation Inequality for the Gaussian Measure". The Annals of Probability 27 (4): 1939–1951. doi:10.1214/aop/1022874822. https://projecteuclid.org/journals/annals-of-probability/volume-27/issue-4/A-Particular-Case-of-Correlation-Inequality-for-the-Gaussian-Measure/10.1214/aop/1022874822.pdf.
- ↑ Royen, Thomas (November 2014). "A simple proof of the Gaussian correlation conjecture extended to multivariate gamma distributions". Far East Journal of Theoretical Statistics 48 (2): 139–145. http://www.pphmj.com/abstract/8713.htm.
- ↑ "Pushpa Publishing House". http://www.pphmj.com/abstract/8713.htm.
- ↑ Latała, R.; Matlak, D. (2017). "Royen's Proof of the Gaussian Correlation Inequality". Geometric Aspects of Functional Analysis. Lecture Notes in Mathematics. 2169. pp. 265–275. doi:10.1007/978-3-319-45282-1_17. ISBN 978-3-319-45281-4.
- ↑ Farand, Chloe (2017-04-03). "Retired man solves one of hardest maths problems in the world and no one notices" (in en-GB). The Independent. https://www.independent.co.uk/news/science/german-man-thomas-royen-solve-maths-problem-gaussian-correlation-inequality-retired-67-age-a7663936.html.
- ↑ Dambeck, Holger (2017-04-04). "Erfolg mit 67 Jahren: Der Wunderopa der Mathematik". http://www.spiegel.de/wissenschaft/mensch/mathematiker-thomas-royen-beweist-mit-67-jahren-statistikproblem-gci-a-1141709.html.
External links
- George Lowther, The Gaussian Correlation Conjecture, "Almost Sure"
 |