Opposite group
In group theory, a branch of mathematics, an opposite group is a way to construct a group from another group that allows one to define right action as a special case of left action.
Monoids, groups, rings, and algebras can be viewed as categories with a single object. The construction of the opposite category generalizes the opposite group, opposite ring, etc.
Definition
Let [math]\displaystyle{ G }[/math] be a group under the operation [math]\displaystyle{ * }[/math]. The opposite group of [math]\displaystyle{ G }[/math], denoted [math]\displaystyle{ G^{\mathrm{op}} }[/math], has the same underlying set as [math]\displaystyle{ G }[/math], and its group operation [math]\displaystyle{ \mathbin{\ast'} }[/math] is defined by [math]\displaystyle{ g_1 \mathbin{\ast'} g_2 = g_2 * g_1 }[/math].
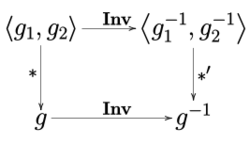
If [math]\displaystyle{ G }[/math] is abelian, then it is equal to its opposite group. Also, every group [math]\displaystyle{ G }[/math] (not necessarily abelian) is naturally isomorphic to its opposite group: An isomorphism [math]\displaystyle{ \varphi: G \to G^{\mathrm{op}} }[/math] is given by [math]\displaystyle{ \varphi(x) = x^{-1} }[/math]. More generally, any antiautomorphism [math]\displaystyle{ \psi: G \to G }[/math] gives rise to a corresponding isomorphism [math]\displaystyle{ \psi': G \to G^{\mathrm{op}} }[/math] via [math]\displaystyle{ \psi'(g)=\psi(g) }[/math], since
- [math]\displaystyle{ \psi'(g * h) = \psi(g * h) = \psi(h) * \psi(g) = \psi(g) \mathbin{\ast'} \psi(h)=\psi'(g) \mathbin{\ast'} \psi'(h). }[/math]
Group action
Let [math]\displaystyle{ X }[/math] be an object in some category, and [math]\displaystyle{ \rho: G \to \mathrm{Aut}(X) }[/math] be a right action. Then [math]\displaystyle{ \rho^{\mathrm{op}}: G^{\mathrm{op}} \to \mathrm{Aut}(X) }[/math] is a left action defined by [math]\displaystyle{ \rho^{\mathrm{op}}(g)x = x\rho(g) }[/math], or [math]\displaystyle{ g^{\mathrm{op}}x = xg }[/math].
See also
External links
 |

