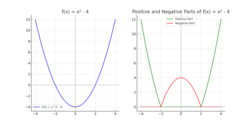
Positive and negative parts

Short description: Decomposition of real-valued functions

Positive and Negative Parts of f(x) = x² - 4

In mathematics, the positive part of a real or extended real-valued function is defined by the formula

[math]\displaystyle{ f^+(x) = \max(f(x),0) = \begin{cases} f(x) & \mbox{ if } f(x) \gt 0 \\ 0 & \mbox{ otherwise.} \end{cases} }[/math]

Intuitively, the graph of [math]\displaystyle{ f^+ }[/math] is obtained by taking the graph of [math]\displaystyle{ f }[/math], chopping off the part under the x-axis, and letting [math]\displaystyle{ f^+ }[/math] take the value zero there.

Similarly, the negative part of f is defined as

[math]\displaystyle{ f^-(x) =\max(-f(x),0)= -\min(f(x),0) = \begin{cases} -f(x) & \mbox{ if } f(x) \lt 0 \\ 0 & \mbox{ otherwise.} \end{cases} }[/math]

Note that both f⁺ and f⁻ are non-negative functions. A peculiarity of terminology is that the 'negative part' is neither negative nor a part (like the imaginary part of a complex number is neither imaginary nor a part).

The function f can be expressed in terms of f⁺ and f⁻ as

[math]\displaystyle{ f = f^+ - f^-. }[/math]

Also note that

[math]\displaystyle{ |f| = f^+ + f^- }[/math].

Using these two equations one may express the positive and negative parts as

[math]\displaystyle{ f^+= \frac{|f| + f}{2} }[/math]

[math]\displaystyle{ f^-= \frac{|f| - f}{2}. }[/math]

Another representation, using the Iverson bracket is

[math]\displaystyle{ f^+= [f\gt 0]f }[/math]

[math]\displaystyle{ f^-= -[f\lt 0]f. }[/math]

One may define the positive and negative part of any function with values in a linearly ordered group.

The unit ramp function is the positive part of the identity function.

Measure-theoretic properties

Given a measurable space (X,Σ), an extended real-valued function f is measurable if and only if its positive and negative parts are. Therefore, if such a function f is measurable, so is its absolute value |f|, being the sum of two measurable functions. The converse, though, does not necessarily hold: for example, taking f as

[math]\displaystyle{ f=1_V-{1\over2}, }[/math]

where V is a Vitali set, it is clear that f is not measurable, but its absolute value is, being a constant function.

The positive part and negative part of a function are used to define the Lebesgue integral for a real-valued function. Analogously to this decomposition of a function, one may decompose a signed measure into positive and negative parts — see the Hahn decomposition theorem.

See also

• Rectifier (neural networks)
• Even and odd functions
• Real and imaginary parts

References

• Jones, Frank (2001). Lebesgue integration on Euclidean space, Rev. ed. Sudbury, Mass.: Jones and Bartlett. ISBN 0-7637-1708-8. 

• Hunter, John K; Nachtergaele, Bruno (2001). Applied analysis. Singapore; River Edge, NJ: World Scientific. ISBN 981-02-4191-7. 

• Rana, Inder K (2002). An introduction to measure and integration, 2nd ed. Providence, R.I.: American Mathematical Society. ISBN 0-8218-2974-2. 

External links

• Positive part on MathWorld