Weighted automaton

Short description: Finite-state machine where edges carry weights

Hasse diagram of some classes of quantitative automata, ordered by expressiveness.

In theoretical computer science and formal language theory, a weighted automaton or weighted finite-state machine is a generalization of a finite-state machine in which the edges have weights, for example real numbers or integers. Finite-state machines are only capable of answering decision problems; they take as input a string and produce a Boolean output, i.e. either "accept" or "reject". In contrast, weighted automata produce a quantitative output, for example a count of how many answers are possible on a given input string, or a probability of how likely the input string is according to a probability distribution. They are one of the simplest studied models of quantitative automata.

The definition of a weighted automaton is generally given over an arbitrary semiring [math]\displaystyle{ R }[/math], an abstract set with an addition operation [math]\displaystyle{ + }[/math] and a multiplication operation [math]\displaystyle{ \times }[/math]. The automaton consists of a finite set of states, a finite input alphabet of characters [math]\displaystyle{ \Sigma }[/math] and edges which are labeled with both a character in [math]\displaystyle{ \Sigma }[/math] and a weight in [math]\displaystyle{ R }[/math]. The weight of any path in the automaton is defined to be the product of weights along the path, and the weight of a string is the sum of the weights of all paths which are labeled with that string. The weighted automaton thus defines a function from [math]\displaystyle{ \Sigma^* }[/math] to [math]\displaystyle{ R }[/math].

Weighted automata generalize deterministic finite automata (DFAs) and nondeterministic finite automata (NFAs), which correspond to weighted automata over the Boolean semiring, where addition is logical disjunction and multiplication is logical conjunction. In the DFA case, there is only one accepting path for any input string, so disjunction is not applied. When the weights are real numbers and the outgoing weights for each state add to one, weighted automata can be considered a probabilistic model and are also known as probabilistic automata. These machines define a probability distribution over all strings, and are related to other probabilistic models such as Markov decision processes and Markov chains.

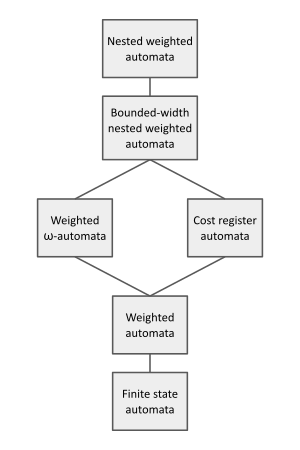
Weighted automata have applications in natural language processing where they are used to assign weights to words and sentences, as well as in image compression. They were first introduced by Marcel-Paul Schützenberger in his 1961 paper On the definition of a family of automata. Since their introduction, many extensions have been proposed, for example nested weighted automata, cost register automata, and weighted finite-state transducers. Researchers have studied weighted automata from the perspective of learning a machine from its input-output behavior (see computational learning theory) and studying decidability questions.

Definition

A commutative semiring (or rig) is a set R equipped with two distinguished elements [math]\displaystyle{ 0 \ne 1 }[/math] and addition and multiplication operations [math]\displaystyle{ \oplus }[/math] and [math]\displaystyle{ \otimes }[/math] such that [math]\displaystyle{ \oplus }[/math] is commutative and associative with identity [math]\displaystyle{ 0 }[/math], [math]\displaystyle{ \otimes }[/math] is commutative and associative with identity [math]\displaystyle{ 1 }[/math], [math]\displaystyle{ \otimes }[/math] distributes over [math]\displaystyle{ \oplus }[/math], and 0 is an absorbing element for [math]\displaystyle{ \otimes }[/math].

A weighted automaton over [math]\displaystyle{ R }[/math] is a tuple [math]\displaystyle{ \mathcal{A} = (Q, \Sigma, \Delta, I, F) }[/math] where:

• [math]\displaystyle{ Q }[/math] is a finite set of states.
• [math]\displaystyle{ \Sigma }[/math] is a finite alphabet.
• [math]\displaystyle{ \Delta \subseteq Q \times \Sigma \times R \times Q }[/math] is a finite set of transitions [math]\displaystyle{ (q, \sigma, w, q') }[/math], where [math]\displaystyle{ \sigma }[/math] is called a character and [math]\displaystyle{ w }[/math] is called a weight.
• [math]\displaystyle{ I: Q \to R }[/math] is an initial weight function.
• [math]\displaystyle{ F: Q \to R }[/math] is a final weight function.

A path on input [math]\displaystyle{ w \in \Sigma^* }[/math] is a finite path in the graph, where the concatenation of the character labels equals [math]\displaystyle{ w }[/math]. The weight of the path [math]\displaystyle{ q_0, q_1, \ldots, q_n }[/math] is the product ([math]\displaystyle{ \otimes }[/math]) of the weights along the path, additionally multiplied by the initial and final weights [math]\displaystyle{ I(q_0) \otimes I(q_n) }[/math]. The weight of the word [math]\displaystyle{ w }[/math] is the sum ([math]\displaystyle{ \oplus }[/math]) of the weights of all paths on input [math]\displaystyle{ w }[/math] (or 0 if there are no accepting paths). In this way the machine defines a function [math]\displaystyle{ [\![ \mathcal{A} ]\!]: \Sigma^* \to R }[/math].

The underlying NFA of [math]\displaystyle{ \mathcal{A} }[/math] is an NFA formed by removing all transitions with weight [math]\displaystyle{ 0 }[/math] and then erasing all of the weights on the transitions [math]\displaystyle{ \Delta }[/math], so that the new transition set lies in [math]\displaystyle{ Q \times \Sigma \times Q }[/math]. The initial states and final states are the set of states [math]\displaystyle{ q }[/math] such that [math]\displaystyle{ I(q) \ne 0 }[/math] and [math]\displaystyle{ F(q) \ne 0 }[/math], respectively.

Variations

• A weighted automaton is deterministic if the underlying NFA is deterministic and unambiguous if the underlying NFA is unambiguous. In these cases, there is always exactly one accepting path, so the [math]\displaystyle{ \oplus }[/math] operation is never applied and can be omitted from the definition.

• It is possible to extend the definition to allow epsilon transitions [math]\displaystyle{ (q, \epsilon, w, q') }[/math], where [math]\displaystyle{ \epsilon }[/math] is the empty string. In this case, one must then require that there are no cycles of epsilon transitions. This does not increase the expressiveness of weighted automata. If epsilon transitions are allowed, the initial weights and final weights can be replaced by initial and final sets of states without loss of expressiveness.

• The transition function can be given as a matrix [math]\displaystyle{ \Delta_\sigma \in R^{Q \times Q} }[/math] with entries in [math]\displaystyle{ R }[/math] for each [math]\displaystyle{ \sigma }[/math], rather than a set of transitions. The entry of the matrix at [math]\displaystyle{ (q, q') }[/math] is the sum of all transitions labeled [math]\displaystyle{ (q, \sigma, q') }[/math].

• Some authors omit the initial and final weight functions [math]\displaystyle{ I }[/math] and [math]\displaystyle{ F }[/math]. Instead, [math]\displaystyle{ I }[/math] and [math]\displaystyle{ F }[/math] are replaced by a set of initial and final states. If epsilon transitions are not present, this technically decreases expressiveness as it forces [math]\displaystyle{ [\![ \mathcal{A} ]\!](\varepsilon) }[/math] to depend only on the number of states that are both initial and final.

• Some authors restrict to specific semirings, such as [math]\displaystyle{ \mathbb{N} }[/math] or [math]\displaystyle{ \mathbb{Z} }[/math], particularly when studying decidability results.

• The requirement that there is a zero element for [math]\displaystyle{ \oplus }[/math] is sometimes omitted; in this case the machine defines a partial function from [math]\displaystyle{ \Sigma^* }[/math] to [math]\displaystyle{ R }[/math] rather than a total function.