Adaptive coordinate descent
Adaptive coordinate descent[1] is an improvement of the coordinate descent algorithm to non-separable optimization by the use of adaptive encoding.[2] The adaptive coordinate descent approach gradually builds a transformation of the coordinate system such that the new coordinates are as decorrelated as possible with respect to the objective function. The adaptive coordinate descent was shown to be competitive to the state-of-the-art evolutionary algorithms and has the following invariance properties:
- Invariance with respect to monotonous transformations of the function (scaling)
- Invariance with respect to orthogonal transformations of the search space (rotation).
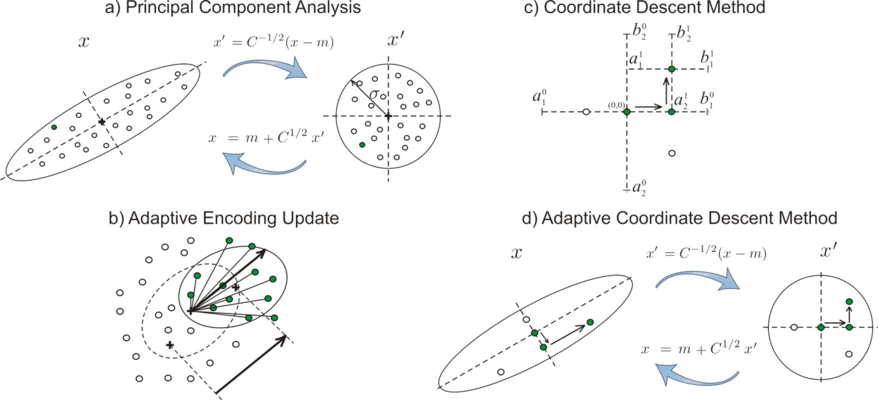
CMA-like Adaptive Encoding Update (b) mostly based on principal component analysis (a) is used to extend the coordinate descent method (c) to the optimization of non-separable problems (d).
The adaptation of an appropriate coordinate system allows adaptive coordinate descent to outperform coordinate descent on non-separable functions. The following figure illustrates the convergence of both algorithms on 2-dimensional Rosenbrock function up to a target function value , starting from the initial point .
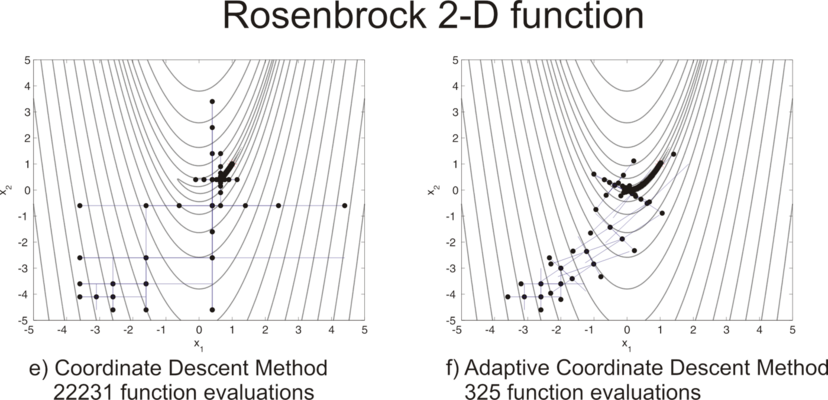
The adaptive coordinate descent method reaches the target value after only 325 function evaluations (about 70 times faster than coordinate descent), that is comparable to gradient-based methods. The algorithm has linear time complexity if update coordinate system every D iterations, it is also suitable for large-scale (D>>100) non-linear optimization.
Relevant approaches
First approaches to optimization using adaptive coordinate system were proposed already in the 1960s (see, e.g., Rosenbrock's method). PRincipal Axis (PRAXIS) algorithm, also referred to as Brent's algorithm, is a derivative-free algorithm which assumes quadratic form of the optimized function and repeatedly updates a set of conjugate search directions.[3] The algorithm, however, is not invariant to scaling of the objective function and may fail under its certain rank-preserving transformations (e.g., will lead to a non-quadratic shape of the objective function). A recent analysis of PRAXIS can be found in.[4] For practical applications see,[5] where an adaptive coordinate descent approach with step-size adaptation and local coordinate system rotation was proposed for robot-manipulator path planning in 3D space with static polygonal obstacles.
See also
References
- ↑ Loshchilov, I.; M. Schoenauer; M. Sebag (2011). "Adaptive Coordinate Descent". ACM Press. pp. 885–892. http://www.loshchilov.com/publications/GECCO2011_AdaptiveCoordinateDescent.pdf.
- ↑ Nikolaus Hansen. "Adaptive Encoding: How to Render Search Coordinate System Invariant". Parallel Problem Solving from Nature - PPSN X, Sep 2008, Dortmund, Germany. pp.205-214, 2008.
- ↑ Brent, R.P. (1972). Prentice-Hall.
- ↑ Ali, U.; Kickmeier-Rust, M.D. (2008). "Implementation and Applications of a Three-Round User Strategy for Improved Principal Axis Minimization". pp. 505–513.
- ↑ Pavlov, D. (2006). "Manipulator path planning in 3-dimensional space". Springer. pp. 505–513.
External links
- SOURCE CODE ACD ACD is a MATLAB source code for Adaptive Coordinate Descent
 |
