Amoeba (mathematics)

Short description: Set associated with a complex-valued polynomial

The amoeba of [math]\displaystyle{ P(z,w) = w - 2z - 1. }[/math]

The amoeba of [math]\displaystyle{ P(z,w) = 3z^2 + 5zw + w^3 + 1. }[/math] Notice the "vacuole" in the middle of the amoeba.

The amoeba of [math]\displaystyle{ P(z,w) = 1 + z + z^2 + z^3 + z^2 w^3 + 10zw + 12z^2 w + 10z^2 w^2. }[/math]

The amoeba of [math]\displaystyle{ P(z,w) = 50z^3 + 83z^2 w + 24zw^2 + w^3 + 392z^2 + 414zw + 50w^2 - 28z + 59w - 100. }[/math]

Points in the amoeba of [math]\displaystyle{ P(x,y,z) = x + y + z - 1. }[/math] Note that the amoeba is actually 3-dimensional, and not a surface (this is not entirely evident from the image).

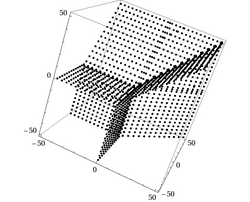
In complex analysis, a branch of mathematics, an amoeba is a set associated with a polynomial in one or more complex variables. Amoebas have applications in algebraic geometry, especially tropical geometry.

Definition

Consider the function

[math]\displaystyle{ \operatorname{Log}: \big({\mathbb C} \setminus \{0\}\big)^n \to \mathbb R^n }[/math]

defined on the set of all n-tuples [math]\displaystyle{ z = (z_1, z_2, \dots, z_n) }[/math] of non-zero complex numbers with values in the Euclidean space [math]\displaystyle{ \mathbb R^n, }[/math] given by the formula

[math]\displaystyle{ \operatorname{Log}(z_1, z_2, \dots, z_n) = \big(\log|z_1|, \log|z_2|, \dots, \log|z_n|\big). }[/math]

Here, log denotes the natural logarithm. If p(z) is a polynomial in [math]\displaystyle{ n }[/math] complex variables, its amoeba [math]\displaystyle{ \mathcal A_p }[/math] is defined as the image of the set of zeros of p under Log, so

[math]\displaystyle{ \mathcal A_p = \left\{\operatorname{Log}(z) : z \in \big(\mathbb C \setminus \{0\}\big)^n, p(z) = 0\right\}. }[/math]

Amoebas were introduced in 1994 in a book by Gelfand, Kapranov, and Zelevinsky.

Properties

Let [math]\displaystyle{ V \subset (\mathbb{C}^{*})^{n} }[/math] be the zero locus of a polynomial

[math]\displaystyle{ f(z) = \sum_{j \in A}a_{j}z^{j} }[/math]

where [math]\displaystyle{ A \subset \mathbb{Z}^{n} }[/math] is finite, [math]\displaystyle{ a_{j} \in \mathbb{C} }[/math] and [math]\displaystyle{ z^{j} = z_{1}^{j_{1}}\cdots z_{n}^{j_{n}} }[/math] if [math]\displaystyle{ z = (z_{1},\dots,z_{n}) }[/math] and [math]\displaystyle{ j = (j_{1},\dots,j_{n}) }[/math]. Let [math]\displaystyle{ \Delta_{f} }[/math] be the Newton polyhedron of [math]\displaystyle{ f }[/math], i.e.,

[math]\displaystyle{ \Delta_{f} = \text{Convex Hull}\{j \in A \mid a_{j} \ne 0\}. }[/math]

Then

• Any amoeba is a closed set.
• Any connected component of the complement [math]\displaystyle{ \mathbb R^n \setminus \mathcal A_p }[/math] is convex.
• The area of an amoeba of a not identically zero polynomial in two complex variables is finite.
• A two-dimensional amoeba has a number of "tentacles", which are infinitely long and exponentially narrow towards infinity.
• The number of connected components of the complement [math]\displaystyle{ \mathbb{R}^{n} \setminus \mathcal{A}_{p} }[/math] is not greater than [math]\displaystyle{ \#(\Delta_{f} \cap \mathbb{Z}^{n}) }[/math] and not less than the number of vertices of [math]\displaystyle{ \Delta_{f} }[/math].
• There is an injection from the set of connected components of complement [math]\displaystyle{ \mathbb{R}^{n} \setminus \mathcal{A}_{p} }[/math] to [math]\displaystyle{ \Delta_{f} \cap \mathbb{Z}^{n} }[/math]. The vertices of [math]\displaystyle{ \Delta_{f} }[/math] are in the image under this injection. A connected component of complement [math]\displaystyle{ \mathbb{R}^{n} \setminus \mathcal{A}_{p} }[/math] is bounded if and only if its image is in the interior of [math]\displaystyle{ \Delta_{f} }[/math].
• If [math]\displaystyle{ V \subset (\mathbb{C}^{*})^{2} }[/math], then the area of [math]\displaystyle{ \mathcal{A}_{p}(V) }[/math] is not greater than [math]\displaystyle{ \pi^{2}\text{Area}(\Delta_{f}) }[/math].

Ronkin function

A useful tool in studying amoebas is the Ronkin function. For p(z), a polynomial in n complex variables, one defines the Ronkin function

[math]\displaystyle{ N_p : \mathbb R^n \to \mathbb R }[/math]

by the formula

[math]\displaystyle{ N_p(x) = \frac{1}{(2\pi i)^n} \int_{\operatorname{Log}^{-1}(x)} \log|p(z)| \,\frac{dz_1}{z_1} \wedge \frac{dz_2}{z_2} \wedge \cdots \wedge \frac{dz_n}{z_n}, }[/math]

where [math]\displaystyle{ x }[/math] denotes [math]\displaystyle{ x = (x_1, x_2, \dots, x_n). }[/math] Equivalently, [math]\displaystyle{ N_p }[/math] is given by the integral

[math]\displaystyle{ N_p(x) = \frac{1}{(2\pi)^n} \int_{[0, 2\pi]^n} \log|p(z)| \,d\theta_1 \,d\theta_2 \cdots d\theta_n, }[/math]

where

[math]\displaystyle{ z = \left(e^{x_1+i\theta_1}, e^{x_2+i\theta_2}, \dots, e^{x_n+i\theta_n}\right). }[/math]

The Ronkin function is convex and affine on each connected component of the complement of the amoeba of [math]\displaystyle{ p(z) }[/math].

As an example, the Ronkin function of a monomial

[math]\displaystyle{ p(z) = a z_1^{k_1} z_2^{k_2} \dots z_n^{k_n} }[/math]

with [math]\displaystyle{ a \ne 0 }[/math] is

[math]\displaystyle{ N_p(x) = \log|a| + k_1 x_1 + k_2 x_2 + \cdots + k_n x_n. }[/math]

References

• Itenberg, Ilia; Mikhalkin, Grigory; Shustin, Eugenii (2007). Tropical algebraic geometry. Oberwolfach Seminars. 35. Basel: Birkhäuser. ISBN 978-3-7643-8309-1. 
• Viro, Oleg (2002), "What Is ... An Amoeba?", Notices of the American Mathematical Society 49 (8): 916–917, https://www.ams.org/notices/200208/what-is.pdf .

Further reading

• Theobald, Thorsten (2002). "Computing amoebas". Exp. Math. 11 (4): 513–526. doi:10.1080/10586458.2002.10504703. https://eudml.org/doc/52814. 

External links

• Amoebas of algebraic varieties