Astronomy:Bi-elliptic transfer
In astronautics and aerospace engineering, the bi-elliptic transfer is an orbital maneuver that moves a spacecraft from one orbit to another and may, in certain situations, require less delta-v than a Hohmann transfer maneuver.
| Part of a series on |
| Astrodynamics |
|---|
 |
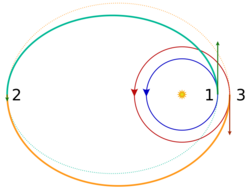
The bi-elliptic transfer consists of two half-elliptic orbits. From the initial orbit, a first burn expends delta-v to boost the spacecraft into the first transfer orbit with an apoapsis at some point [math]\displaystyle{ r_b }[/math] away from the central body. At this point a second burn sends the spacecraft into the second elliptical orbit with periapsis at the radius of the final desired orbit, where a third burn is performed, injecting the spacecraft into the desired orbit.[1]
While they require one more engine burn than a Hohmann transfer and generally require a greater travel time, some bi-elliptic transfers require a lower amount of total delta-v than a Hohmann transfer when the ratio of final to initial semi-major axis is 11.94 or greater, depending on the intermediate semi-major axis chosen.[2]
The idea of the bi-elliptical transfer trajectory was first[citation needed] published by Ary Sternfeld in 1934.[3]
Calculation
Delta-v
The three required changes in velocity can be obtained directly from the vis-viva equation [math]\displaystyle{ v^2 = \mu \left( \frac{2}{r} - \frac{1}{a} \right), }[/math] where
- [math]\displaystyle{ v }[/math] is the speed of an orbiting body,
- [math]\displaystyle{ \mu = GM }[/math] is the standard gravitational parameter of the primary body,
- [math]\displaystyle{ r }[/math] is the distance of the orbiting body from the primary, i.e., the radius,
- [math]\displaystyle{ a }[/math] is the semi-major axis of the body's orbit.
In what follows,
- [math]\displaystyle{ r_1 }[/math] is the radius of the initial circular orbit,
- [math]\displaystyle{ r_2 }[/math] is the radius of the final circular orbit,
- [math]\displaystyle{ r_b }[/math] is the common apoapsis radius of the two transfer ellipses and is a free parameter of the maneuver,
- [math]\displaystyle{ a_1 }[/math] and [math]\displaystyle{ a_2 }[/math] are the semimajor axes of the two elliptical transfer orbits, which are given by [math]\displaystyle{ a_1 = \frac{r_1 + r_b}{2}, }[/math] and [math]\displaystyle{ a_2 = \frac{r_2 + r_b}{2}. }[/math]
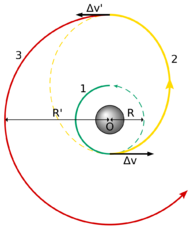
Starting from the initial circular orbit with radius [math]\displaystyle{ r_1 }[/math] (dark blue circle in the figure to the right), a prograde burn (mark 1 in the figure) puts the spacecraft on the first elliptical transfer orbit (aqua half-ellipse). The magnitude of the required delta-v for this burn is [math]\displaystyle{ \Delta v_1 = \sqrt{ \frac{2 \mu}{r_1} - \frac{\mu}{a_1}} - \sqrt{\frac{\mu}{r_1}}. }[/math]
When the apoapsis of the first transfer ellipse is reached at a distance [math]\displaystyle{ r_b }[/math] from the primary, a second prograde burn (mark 2) raises the periapsis to match the radius of the target circular orbit, putting the spacecraft on a second elliptic trajectory (orange half-ellipse). The magnitude of the required delta-v for the second burn is [math]\displaystyle{ \Delta v_2 = \sqrt{\frac{2 \mu}{r_b} - \frac{\mu}{a_2}} - \sqrt{\frac{2 \mu}{r_b} - \frac{\mu}{a_1}}. }[/math]
Lastly, when the final circular orbit with radius [math]\displaystyle{ r_2 }[/math] is reached, a retrograde burn (mark 3) circularizes the trajectory into the final target orbit (red circle). The final retrograde burn requires a delta-v of magnitude [math]\displaystyle{ \Delta v_3 = \sqrt{\frac{2 \mu}{r_2} - \frac{\mu}{a_2}} - \sqrt{\frac{\mu}{r_2}}. }[/math]
If [math]\displaystyle{ r_b = r_2 }[/math], then the maneuver reduces to a Hohmann transfer (in that case [math]\displaystyle{ \Delta v_3 }[/math] can be verified to become zero). Thus the bi-elliptic transfer constitutes a more general class of orbital transfers, of which the Hohmann transfer is a special two-impulse case.
The maximal possible savings can be computed by assuming that [math]\displaystyle{ r_b = \infty }[/math], in which case the total [math]\displaystyle{ \Delta v }[/math] simplifies to [math]\displaystyle{ \sqrt{\mu/r_1} \left(\sqrt{2} - 1\right) \left(1 + \sqrt{r_1/r_2}\right) }[/math]. In this case, one also speaks of a bi-parabolic transfer because the two transfer trajectories are no longer ellipses but parabolas. The transfer time increases to infinity too.
Transfer time
Like the Hohmann transfer, both transfer orbits used in the bi-elliptic transfer constitute exactly one half of an elliptic orbit. This means that the time required to execute each phase of the transfer is half the orbital period of each transfer ellipse.
Using the equation for the orbital period and the notation from above, [math]\displaystyle{ T = 2 \pi \sqrt{\frac{a^3}{\mu}}. }[/math]
The total transfer time [math]\displaystyle{ t }[/math] is the sum of the times required for each half-orbit. Therefore: [math]\displaystyle{ t_1 = \pi \sqrt{\frac{a_1^3}{\mu}} \quad \text{and} \quad t_2 = \pi \sqrt{\frac{a_2^3}{\mu}}, }[/math] and finally: [math]\displaystyle{ t = t_1 + t_2. }[/math]
Comparison with the Hohmann transfer
Delta-v
The figure shows the total [math]\displaystyle{ \Delta v }[/math] required to transfer from a circular orbit of radius [math]\displaystyle{ r_1 }[/math] to another circular orbit of radius [math]\displaystyle{ r_2 }[/math]. The [math]\displaystyle{ \Delta v }[/math] is shown normalized to the orbital speed in the initial orbit, [math]\displaystyle{ v_1 }[/math], and is plotted as a function of the ratio of the radii of the final and initial orbits, [math]\displaystyle{ R \equiv r_2 / r_1 }[/math]; this is done so that the comparison is general (i.e. not dependent of the specific values of [math]\displaystyle{ r_1 }[/math] and [math]\displaystyle{ r_2 }[/math], only on their ratio).[2]
The thick black curve indicates the [math]\displaystyle{ \Delta v }[/math] for the Hohmann transfer, while the thinner colored curves correspond to bi-elliptic transfers with varying values of the parameter [math]\displaystyle{ \alpha \equiv r_b / r_1 }[/math], defined as the apoapsis radius [math]\displaystyle{ r_b }[/math] of the elliptic auxiliary orbit normalized to the radius of the initial orbit, and indicated next to the curves. The inset shows a close-up of the region where the bi-elliptic curves cross the Hohmann curve for the first time.
One sees that the Hohmann transfer is always more efficient if the ratio of radii [math]\displaystyle{ R }[/math] is smaller than 11.94. On the other hand, if the radius of the final orbit is more than 15.58 times larger than the radius of the initial orbit, then any bi-elliptic transfer, regardless of its apoapsis radius (as long as it's larger than the radius of the final orbit), requires less [math]\displaystyle{ \Delta v }[/math] than a Hohmann transfer. Between the ratios of 11.94 and 15.58, which transfer is best depends on the apoapsis distance [math]\displaystyle{ r_b }[/math]. For any given [math]\displaystyle{ R }[/math] in this range, there is a value of [math]\displaystyle{ r_b }[/math] above which the bi-elliptic transfer is superior and below which the Hohmann transfer is better. The following table lists the value of [math]\displaystyle{ \alpha \equiv r_b / r_1 }[/math] that results in the bi-elliptic transfer being better for some selected cases.[4]
| Ratio of radii, [math]\displaystyle{ \frac{r_2}{r_1} }[/math] | Minimal [math]\displaystyle{ \alpha \equiv \frac{r_b}{r_1} }[/math] | Comments |
|---|---|---|
| <11.94 | N/A | Hohmann transfer is always better |
| 11.94 | [math]\displaystyle{ \infty }[/math] | Bi-parabolic transfer |
| 12 | 815.81 | |
| 13 | 48.90 | |
| 14 | 26.10 | |
| 15 | 18.19 | |
| 15.58 | 15.58 | |
| >15.58 | [math]\displaystyle{ \gt \frac{r_2}{r_1} }[/math] | Any bi-elliptic transfer is better |
Transfer time
The long transfer time of the bi-elliptic transfer, [math]\displaystyle{ t = \pi\sqrt{\frac{a_1^3}{\mu}} + \pi\sqrt{\frac{a_2^3}{\mu}}, }[/math] is a major drawback for this maneuver. It even becomes infinite for the bi-parabolic transfer limiting case.
The Hohmann transfer takes less than half of the time because there is just one transfer half-ellipse. To be precise, [math]\displaystyle{ t = \pi\sqrt{\frac{a^3}{\mu}}. }[/math]
Versatility in combination maneuvers
While a bi-elliptic transfer has a small parameter window where it's strictly superior to a Hohmann Transfer in terms of delta V for a planar transfer between circular orbits, the savings is fairly small, and a bi-elliptic transfer is a far greater aid when used in combination with certain other maneuvers.
At apoapsis, the spacecraft is travelling at low orbital velocity, and significant changes in periapsis can be achieved for small delta V cost. Transfers that resemble a bi-elliptic but which incorporate a plane-change maneuver at apoapsis can dramatically save delta-V on missions where the plane needs to be adjusted as well as the altitude, versus making the plane change in low circular orbit on top of a Hohmann transfer.
Likewise, dropping periapsis all the way into the atmosphere of a planetary body for aerobraking is inexpensive in velocity at apoapsis, but permits the use of "free" drag to aid in the final circularization burn to drop apoapsis; though it adds an extra mission stage of periapsis-raising back out of the atmosphere, this may, under some parameters, cost significantly less delta V than simply dropping periapsis in one burn from circular orbit.
Example
To transfer from a circular low Earth orbit with r0 = 6700 km to a new circular orbit with r1 = 93 800 km using a Hohmann transfer orbit requires a Δv of 2825.02 + 1308.70 = 4133.72 m/s. However, because r1 = 14r0 > 11.94r0, it is possible to do better with a bi-elliptic transfer. If the spaceship first accelerated 3061.04 m/s, thus achieving an elliptic orbit with apogee at r2 = 40r0 = 268 000 km, then at apogee accelerated another 608.825 m/s to a new orbit with perigee at r1 = 93 800 km, and finally at perigee of this second transfer orbit decelerated by 447.662 m/s, entering the final circular orbit, then the total Δv would be only 4117.53 m/s, which is 16.19 m/s (0.4%) less.
The Δv saving could be further improved by increasing the intermediate apogee, at the expense of longer transfer time. For example, an apogee of 75.8r0 = 507 688 km (1.3 times the distance to the Moon) would result in a 1% Δv saving over a Hohmann transfer, but require a transit time of 17 days. As an impractical extreme example, an apogee of 1757r0 = 11 770 000 km (30 times the distance to the Moon) would result in a 2% Δv saving over a Hohmann transfer, but the transfer would require 4.5 years (and, in practice, be perturbed by the gravitational effects of other Solar system bodies). For comparison, the Hohmann transfer requires 15 hours and 34 minutes.
| Type | Hohmann | Bi-elliptic | ||||
|---|---|---|---|---|---|---|
| Apogee (km) | 93 800 | 268 000 | 507 688 | 11 770 000 | ∞ | |
| Burn (m/s) |
1 | |||||
| 2 | ||||||
| 3 | ||||||
| Total (m/s) | 4133.72 | 4117.53 | 4092.38 | 4051.04 | 4048.76 | |
| Of Hohmann | 100% | 99.6% | 99.0% | 98.0% | 97.94% | |
 Δv applied prograde
Δv applied prograde Δv applied retrograde
Δv applied retrograde
Evidently, the bi-elliptic orbit spends more of its delta-v early on (in the first burn). This yields a higher contribution to the specific orbital energy and, due to the Oberth effect, is responsible for the net reduction in required delta-v.
See also
References
- ↑ Curtis, Howard (2005). Orbital Mechanics for Engineering Students. Elsevier. p. 264. ISBN 0-7506-6169-0. https://books.google.com/books?id=6aO9aGNBAgIC.
- ↑ 2.0 2.1 Vallado, David Anthony (2001). Fundamentals of Astrodynamics and Applications. Springer. p. 318. ISBN 0-7923-6903-3. https://books.google.com/books?id=PJLlWzMBKjkC.
- ↑ Sternfeld, Ary J. (1934-02-12), "Sur les trajectoires permettant d'approcher d'un corps attractif central à partir d'une orbite keplérienne donnée" (in French), Comptes rendus de l'Académie des sciences (Paris) 198 (1): 711–713, http://gallica.bnf.fr/ark:/12148/bpt6k31506/f711.image.langEN.
- ↑ Gobetz, F. W.; Doll, J. R. (May 1969). "A Survey of Impulsive Trajectories". AIAA Journal (American Institute of Aeronautics and Astronautics) 7 (5): 801–834. doi:10.2514/3.5231. Bibcode: 1969AIAAJ...7..801D.
- ↑ Escobal, Pedro R. (1968). Methods of Astrodynamics. New York: John Wiley & Sons. ISBN 978-0-471-24528-5.
 |