Astronomy:Delta-v

Short description: Measure of amount of effort to change trajectory

Delta-v (more known as "change in velocity"), symbolized as [math]\displaystyle{ {\Delta v} }[/math] and pronounced delta-vee, as used in spacecraft flight dynamics, is a measure of the impulse per unit of spacecraft mass that is needed to perform a maneuver such as launching from or landing on a planet or moon, or an in-space orbital maneuver. It is a scalar that has the units of speed. As used in this context, it is not the same as the physical change in velocity of said spacecraft.

A simple example might be the case of a conventional rocket-propelled spacecraft, which achieves thrust by burning fuel. Such a spacecraft's delta-v, then, would be the change in velocity that spacecraft can achieve by burning its entire fuel load.

Delta-v is produced by reaction engines, such as rocket engines, and is proportional to the thrust per unit mass and the burn time. It is used to determine the mass of propellant required for the given maneuver through the Tsiolkovsky rocket equation.

For multiple maneuvers, delta-v sums linearly.

For interplanetary missions, delta-v is often plotted on a porkchop plot, which displays the required mission delta-v as a function of launch date.

Definition

[math]\displaystyle{ \Delta{v} = \int_{t_0}^{t_1} \frac{|T(t)|}{m(t)}\, dt }[/math] where

• T(t) is the instantaneous thrust at time t.
• m(t) is the instantaneous mass at time t.

Specific cases

In the absence of external forces: [math]\displaystyle{ \Delta{v} = \int_{t_0}^{t_1} \left|\dot{v}\right|\, dt }[/math] where [math]\displaystyle{ \dot{v} }[/math] is the coordinate acceleration.

When thrust is applied in a constant direction (v/|v| is constant) this simplifies to: [math]\displaystyle{ \Delta{v} = | v_1 - v_0 | }[/math] which is simply the magnitude of the change in velocity. However, this relation does not hold in the general case: if, for instance, a constant, unidirectional acceleration is reversed after (t₁ − t₀)/2 then the velocity difference is 0, but delta-v is the same as for the non-reversed thrust.

For rockets, "absence of external forces" is taken to mean the absence of gravity and atmospheric drag, as well as the absence of aerostatic back pressure on the nozzle, and hence the vacuum I_sp is used for calculating the vehicle's delta-v capacity via the rocket equation. In addition, the costs for atmospheric losses and gravity drag are added into the delta-v budget when dealing with launches from a planetary surface.

Orbital maneuvers

Orbit maneuvers are made by firing a thruster to produce a reaction force acting on the spacecraft. The size of this force will be

[math]\displaystyle{ T = v_\text{exh}\ \rho }[/math]

(1)

where

• v_exh is the velocity of the exhaust gas in rocket frame
• ρ is the propellant flow rate to the combustion chamber

The acceleration [math]\displaystyle{ \dot{v} }[/math] of the spacecraft caused by this force will be

[math]\displaystyle{ \dot{v} = \frac{T}{m} = v_\text{exh}\ \frac{\rho}{m} }[/math]

(2)

where m is the mass of the spacecraft

During the burn the mass of the spacecraft will decrease due to use of fuel, the time derivative of the mass being

[math]\displaystyle{ \dot{m} = -\rho\, }[/math]

(3)

If now the direction of the force, i.e. the direction of the nozzle, is fixed during the burn one gets the velocity increase from the thruster force of a burn starting at time [math]\displaystyle{ t_0\, }[/math] and ending at t₁ as

[math]\displaystyle{ \Delta{v} = -\int_{t_0}^{t_1} {v_\text{exh}\ \frac{\dot{m}}{m}}\, dt }[/math]

(4)

Changing the integration variable from time t to the spacecraft mass m one gets

[math]\displaystyle{ \Delta{v} = -\int_{m_0}^{m_1} {v_\text{exh}\ \frac{dm}{m}} }[/math]

(5)

Assuming [math]\displaystyle{ v_\text{exh}\, }[/math] to be a constant not depending on the amount of fuel left this relation is integrated to

[math]\displaystyle{ \Delta{v} = v_\text{exh}\ \ln\left(\frac{m_0}{m_1}\right) }[/math]

(6)

which is the Tsiolkovsky rocket equation.

If for example 20% of the launch mass is fuel giving a constant [math]\displaystyle{ v_\text{exh} }[/math] of 2100 m/s (a typical value for a hydrazine thruster) the capacity of the reaction control system is [math]\displaystyle{ \Delta{v} = 2100\ \ln\left(\frac{1}{0.8}\right)\,\text{m/s} = 460\,\text{m/s}. }[/math]

If [math]\displaystyle{ v_\text{exh} }[/math] is a non-constant function of the amount of fuel left [math]\displaystyle{ v_\text{exh} = v_\text{exh}(m) }[/math] the capacity of the reaction control system is computed by the integral (5).

The acceleration (2) caused by the thruster force is just an additional acceleration to be added to the other accelerations (force per unit mass) affecting the spacecraft and the orbit can easily be propagated with a numerical algorithm including also this thruster force. But for many purposes, typically for studies or for maneuver optimization, they are approximated by impulsive maneuvers as illustrated in figure 1 with a [math]\displaystyle{ \Delta{v} }[/math] as given by (4). Like this one can for example use a "patched conics" approach modeling the maneuver as a shift from one Kepler orbit to another by an instantaneous change of the velocity vector.

Figure 1: Approximation of a finite thrust maneuver with an impulsive change in velocity having the delta-v given by (4).

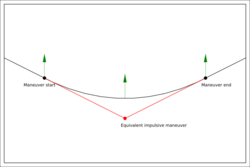
This approximation with impulsive maneuvers is in most cases very accurate, at least when chemical propulsion is used. For low thrust systems, typically electrical propulsion systems, this approximation is less accurate. But even for geostationary spacecraft using electrical propulsion for out-of-plane control with thruster burn periods extending over several hours around the nodes this approximation is fair.

Production

Delta-v is typically provided by the thrust of a rocket engine, but can be created by other engines. The time-rate of change of delta-v is the magnitude of the acceleration caused by the engines, i.e., the thrust per total vehicle mass. The actual acceleration vector would be found by adding thrust per mass on to the gravity vector and the vectors representing any other forces acting on the object.

The total delta-v needed is a good starting point for early design decisions since consideration of the added complexities are deferred to later times in the design process.

The rocket equation shows that the required amount of propellant dramatically increases with increasing delta-v. Therefore, in modern spacecraft propulsion systems considerable study is put into reducing the total delta-v needed for a given spaceflight, as well as designing spacecraft that are capable of producing larger delta-v.

Increasing the delta-v provided by a propulsion system can be achieved by:

• staging
• increasing specific impulse
• improving propellant mass fraction

Multiple maneuvers

Because the mass ratios apply to any given burn, when multiple maneuvers are performed in sequence, the mass ratios multiply.

Thus it can be shown that, provided the exhaust velocity is fixed, this means that delta-v can be summed:

When m₁, m₂ are the mass ratios of the maneuvers, and v₁, v₂ are the delta-v of the first and second maneuvers [math]\displaystyle{ \begin{align} m_1 m_2 &= e^{V_1/V_e} e^{V_2/V_e} \\ &= e^\frac{V_1 + V_2}{V_e} \\ &= e^{V/V_e} = M \end{align} }[/math] where V = v₁ + v₂ and M = m₁ m₂. This is just the rocket equation applied to the sum of the two maneuvers.

This is convenient since it means that delta-v can be calculated and simply added and the mass ratio calculated only for the overall vehicle for the entire mission. Thus delta-v is commonly quoted rather than mass ratios which would require multiplication.

Delta-v budgets

When designing a trajectory, delta-v budget is used as a good indicator of how much propellant will be required. Propellant usage is an exponential function of delta-v in accordance with the rocket equation, it will also depend on the exhaust velocity.

It is not possible to determine delta-v requirements from conservation of energy by considering only the total energy of the vehicle in the initial and final orbits since energy is carried away in the exhaust (see also below). For example, most spacecraft are launched in an orbit with inclination fairly near to the latitude at the launch site, to take advantage of the Earth's rotational surface speed. If it is necessary, for mission-based reasons, to put the spacecraft in an orbit of different inclination, a substantial delta-v is required, though the specific kinetic and potential energies in the final orbit and the initial orbit are equal.

When rocket thrust is applied in short bursts the other sources of acceleration may be negligible, and the magnitude of the velocity change of one burst may be simply approximated by the delta-v. The total delta-v to be applied can then simply be found by addition of each of the delta-v's needed at the discrete burns, even though between bursts the magnitude and direction of the velocity changes due to gravity, e.g. in an elliptic orbit.

For examples of calculating delta-v, see Hohmann transfer orbit, gravitational slingshot, and Interplanetary Transport Network. It is also notable that large thrust can reduce gravity drag.

Delta-v is also required to keep satellites in orbit and is expended in propulsive orbital stationkeeping maneuvers. Since the propellant load on most satellites cannot be replenished, the amount of propellant initially loaded on a satellite may well determine its useful lifetime.

Oberth effect

From power considerations, it turns out that when applying delta-v in the direction of the velocity the specific orbital energy gained per unit delta-v is equal to the instantaneous speed. This is called the Oberth effect.

For example, a satellite in an elliptical orbit is boosted more efficiently at high speed (that is, small altitude) than at low speed (that is, high altitude).

Another example is that when a vehicle is making a pass of a planet, burning the propellant at closest approach rather than further out gives significantly higher final speed, and this is even more so when the planet is a large one with a deep gravity field, such as Jupiter.

See also powered slingshots.

Porkchop plot

Due to the relative positions of planets changing over time, different delta-vs are required at different launch dates. A diagram that shows the required delta-v plotted against time is sometimes called a porkchop plot. Such a diagram is useful since it enables calculation of a launch window, since launch should only occur when the mission is within the capabilities of the vehicle to be employed.

Around the Solar System

Delta-v needed for various orbital manoeuvers using conventional rockets; red arrows show where optional aerobraking can be performed in that particular direction, black numbers give delta-v in km/s that apply in either direction. Lower-delta-v transfers than shown can often be achieved, but involve rare transfer windows or take significantly longer, see: fuzzy orbital transfers.

C3

Escape orbit

GEO

Geosynchronous orbit

GTO

Geostationary transfer orbit

L4/5

Earth–Moon L₄L₅ Lagrangian point

LEO

Low Earth orbit

LEO reentry

For example the Soyuz spacecraft makes a de-orbit from the ISS in two steps. First, it needs a delta-v of 2.18 m/s for a safe separation from the space station. Then it needs another 128 m/s for reentry.

See also

• Delta-v budget
• Gravity drag
• Orbital maneuver
• Orbital stationkeeping
• Spacecraft propulsion
• Specific impulse
• Tsiolkovsky rocket equation
• Delta-v (physics)