Astronomy:Gravity assist
| Part of a series on |
| Astrodynamics |
|---|
 |
A gravity assist, gravity assist maneuver, swing-by, or generally a gravitational slingshot in orbital mechanics, is a type of spaceflight flyby which makes use of the relative movement (e.g. orbit around the Sun) and gravity of a planet or other astronomical object to alter the path and speed of a spacecraft, typically to save propellant and reduce expense.
Gravity assistance can be used to accelerate a spacecraft, that is, to increase or decrease its speed or redirect its path. The "assist" is provided by the motion of the gravitating body as it pulls on the spacecraft.[1] Any gain or loss of kinetic energy and linear momentum by a passing spacecraft is correspondingly lost or gained by the gravitational body, in accordance with Newton's Third Law. The gravity assist maneuver was first used in 1959 when the Soviet probe Luna 3 photographed the far side of Earth's Moon, and it was used by interplanetary probes from Mariner 10 onward, including the two Voyager probes' notable flybys of Jupiter and Saturn.
Explanation

In the planet's frame of reference, the space probe leaves with the exact same speed at which it had arrived. But when observed in the reference frame of the Solar System (fixed to the Sun), the benefit of this maneuver becomes apparent. Here it can be seen how the probe gains speed by tapping energy from the speed of the planet as it orbits the Sun. (If the trajectory is designed to pass in front of the planet instead of behind it, the gravity assist can be used as a braking maneuver rather than accelerating.) Because the mass of the probe is many orders of magnitude smaller than that of the planet, while the result on the probe is quite significant, the deceleration reaction experienced by the planet, according to Newton's third law, is utterly imperceptible.
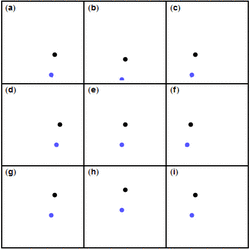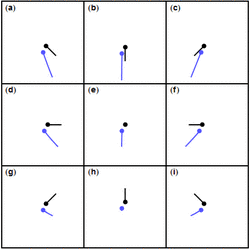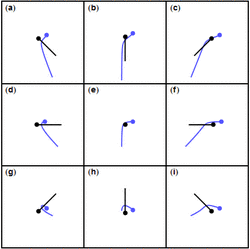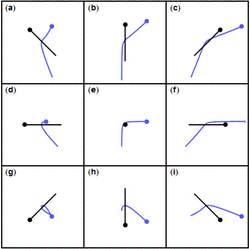
A gravity assist around a planet changes a spacecraft's velocity (relative to the Sun) by entering and leaving the gravitational sphere of influence of a planet. The spacecraft's speed increases as it approaches the planet and decreases as it leaves the planet. To increase speed, the spacecraft approaches the planet in the same direction the planet is orbiting the Sun, and departs in the opposite direction. To decrease speed, the spacecraft approaches the planet traveling the opposite direction from planet's orbital velocity. In both types of maneuver the energy transfer compared to the planet's total orbital energy is negligible. The sum of the kinetic energies of both bodies remains constant (see elastic collision). A slingshot maneuver can therefore be used to change the spaceship's trajectory and speed relative to the Sun.[3]
A close terrestrial analogy is provided by a tennis ball bouncing off the front of a moving train. Imagine standing on a train platform, and throwing a ball at 30 km/h toward a train approaching at 50 km/h. The driver of the train sees the ball approaching at 80 km/h and then departing at 80 km/h after the ball bounces elastically off the front of the train. Because of the train's motion, however, that departure is at 130 km/h relative to the train platform; the ball has added twice the train's velocity to its own.[4]
Translating this analogy into space: in the planet reference frame, the spaceship has a vertical velocity of v relative to the planet. After the slingshot occurs the spaceship is leaving on a course 90 degrees to that which it arrived on. It will still have a velocity of v, but in the horizontal direction.[2] In the Sun reference frame, the planet has a horizontal velocity of v, and by using the Pythagorean Theorem, the spaceship initially has a total velocity of √2v. After the spaceship leaves the planet, it will have a velocity of v + v = 2v, gaining approximately 0.6v.[2]
This oversimplified example is impossible to refine without additional details regarding the orbit, but if the spaceship travels in a path which forms a hyperbola, it can leave the planet in the opposite direction without firing its engine. This example is one of many trajectories and gains of speed the spaceship can experience.
This explanation might seem to violate the conservation of energy and momentum, apparently adding velocity to the spacecraft out of nothing, but the spacecraft's effects on the planet must also be taken into consideration to provide a complete picture of the mechanics involved. The linear momentum gained by the spaceship is equal in magnitude to that lost by the planet, so the spacecraft gains velocity and the planet loses velocity. However, the planet's enormous mass compared to the spacecraft makes the resulting change in its speed negligibly small even when compared to the orbital perturbations planets undergo due to interactions with other celestial bodies on astronomically short timescales. For example, one metric ton is a typical mass for an interplanetary space probe whereas Jupiter has a mass of almost 2 x 1024 metric tons. Therefore, a one-ton spacecraft passing Jupiter will theoretically cause the planet to lose approximately 5 x 10−25 km/s of orbital velocity for every km/s of velocity relative to the Sun gained by the spacecraft. For all practical purposes the effects on the planet can be ignored in the calculation.[5]
Realistic portrayals of encounters in space require the consideration of three dimensions. The same principles apply as above except adding the planet's velocity to that of the spacecraft requires vector addition as shown below.

Due to the reversibility of orbits, gravitational slingshots can also be used to reduce the speed of a spacecraft. Both Mariner 10 and MESSENGER performed this maneuver to reach Mercury.[citation needed]
If more speed is needed than available from gravity assist alone, a rocket burn near the periapsis (closest planetary approach) uses the least fuel. A given rocket burn always provides the same change in velocity (Δv), but the change in kinetic energy is proportional to the vehicle's velocity at the time of the burn. Therefore the maximum kinetic energy is obtained when the burn occurs at the vehicle's maximum velocity (periapsis). The Oberth effect describes this technique in more detail.
Historical origins
In his paper "To Those Who Will Be Reading in Order to Build" ("Тем, кто будет читать, чтобы строить"),[6] published in 1938 but dated 1918–1919,[lower-alpha 1] Yuri Kondratyuk suggested that a spacecraft traveling between two planets could be accelerated at the beginning and end of its trajectory by using the gravity of the two planets' moons. The portion of his manuscript considering gravity-assists received no later development and was not published until the 1960s.[7] In his 1925 paper "Problems of Flight by Jet Propulsion: Interplanetary Flights" ("Проблема полета при помощи реактивных аппаратов: межпланетные полеты"),[8] Friedrich Zander showed a deep understanding of the physics behind the concept of gravity assist and its potential for the interplanetary exploration of the solar system.[7]
Italian engineer Gaetano Crocco was first to calculate an interplanetary journey considering multiple gravity-assists.[7]
The gravity assist maneuver was first used in 1959 when the Soviet probe Luna 3 photographed the far side of the Moon. The maneuver relied on research performed under the direction of Mstislav Keldysh at the Keldysh Institute of Applied Mathematics.[9][10][11][12]
In 1961, Michael Minovitch, UCLA graduate student who worked at NASA's Jet Propulsion Laboratory (JPL), developed a gravity assist technique, that would later be used for the Gary Flandro's Planetary Grand Tour idea.[13][14]
During the summer of 1964 at the NASA JPL, Gary Flandro was assigned the task of studying techniques for exploring the outer planets of the solar system. In this study he discovered the rare alignment of the outer planets (Jupiter, Saturn, Uranus, and Neptune) and conceived the Planetary Grand Tour multi-planet mission utilizing gravity assist to reduce mission duration from forty years to less than ten.[15]
Purpose
A spacecraft traveling from Earth to an inner planet will increase its relative speed because it is falling toward the Sun, and a spacecraft traveling from Earth to an outer planet will decrease its speed because it is leaving the vicinity of the Sun.
Although the orbital speed of an inner planet is greater than that of the Earth, a spacecraft traveling to an inner planet, even at the minimum speed needed to reach it, is still accelerated by the Sun's gravity to a speed notably greater than the orbital speed of that destination planet. If the spacecraft's purpose is only to fly by the inner planet, then there is typically no need to slow the spacecraft. However, if the spacecraft is to be inserted into orbit about that inner planet, then there must be some way to slow it down.
Similarly, while the orbital speed of an outer planet is less than that of the Earth, a spacecraft leaving the Earth at the minimum speed needed to travel to some outer planet is slowed by the Sun's gravity to a speed far less than the orbital speed of that outer planet. Therefore, there must be some way to accelerate the spacecraft when it reaches that outer planet if it is to enter orbit about it.
Rocket engines can certainly be used to increase and decrease the speed of the spacecraft. However, rocket thrust takes propellant, propellant has mass, and even a small change in velocity (known as Δv, or "delta-v", the delta symbol being used to represent a change and "v" signifying velocity) translates to a far larger requirement for propellant needed to escape Earth's gravity well. This is because not only must the primary-stage engines lift the extra propellant, they must also lift the extra propellant beyond that which is needed to lift that additional propellant. The liftoff mass requirement increases exponentially with an increase in the required delta-v of the spacecraft.
Because additional fuel is needed to lift fuel into space, space missions are designed with a tight propellant "budget", known as the "delta-v budget". The delta-v budget is in effect the total propellant that will be available after leaving the earth, for speeding up, slowing down, stabilization against external buffeting (by particles or other external effects), or direction changes, if it cannot acquire more propellant. The entire mission must be planned within that capability. Therefore, methods of speed and direction change that do not require fuel to be burned are advantageous, because they allow extra maneuvering capability and course enhancement, without spending fuel from the limited amount which has been carried into space. Gravity assist maneuvers can greatly change the speed of a spacecraft without expending propellant, and can save significant amounts of propellant, so they are a very common technique to save fuel.
Limits
The main practical limit to the use of a gravity assist maneuver is that planets and other large masses are seldom in the right places to enable a voyage to a particular destination. For example, the Voyager missions which started in the late 1970s were made possible by the "Grand Tour" alignment of Jupiter, Saturn, Uranus and Neptune. A similar alignment will not occur again until the middle of the 22nd century. That is an extreme case, but even for less ambitious missions there are years when the planets are scattered in unsuitable parts of their orbits.[citation needed]
Another limitation is the atmosphere, if any, of the available planet. The closer the spacecraft can approach, the faster its periapsis speed as gravity accelerates the spacecraft, allowing for more kinetic energy to be gained from a rocket burn. However, if a spacecraft gets too deep into the atmosphere, the energy lost to drag can exceed that gained from the planet's gravity. On the other hand, the atmosphere can be used to accomplish aerobraking. There have also been theoretical proposals to use aerodynamic lift as the spacecraft flies through the atmosphere. This maneuver, called an aerogravity assist, could bend the trajectory through a larger angle than gravity alone, and hence increase the gain in energy.[citation needed]
Even in the case of an airless body, there is a limit to how close a spacecraft may approach. The magnitude of the achievable change in velocity depends on the spacecraft's approach velocity and the planet's escape velocity at the point of closest approach (limited by either the surface or the atmosphere.)[citation needed]
Interplanetary slingshots using the Sun itself are not possible because the Sun is at rest relative to the Solar System as a whole. However, thrusting when near the Sun has the same effect as the powered slingshot described as the Oberth effect. This has the potential to magnify a spacecraft's thrusting power enormously, but is limited by the spacecraft's ability to resist the heat.[citation needed]
A rotating black hole might provide additional assistance, if its spin axis is aligned the right way. General relativity predicts that a large spinning mass produces frame-dragging—close to the object, space itself is dragged around in the direction of the spin. Any ordinary rotating object produces this effect. Although attempts to measure frame dragging about the Sun have produced no clear evidence, experiments performed by Gravity Probe B have detected frame-dragging effects caused by Earth.[16] General relativity predicts that a spinning black hole is surrounded by a region of space, called the ergosphere, within which standing still (with respect to the black hole's spin) is impossible, because space itself is dragged at the speed of light in the same direction as the black hole's spin. The Penrose process may offer a way to gain energy from the ergosphere, although it would require the spaceship to dump some "ballast" into the black hole, and the spaceship would have had to expend energy to carry the "ballast" to the black hole.[citation needed]
Notable examples of use
- Luna 3
The gravity assist maneuver was first attempted in 1959 for Luna 3, to photograph the far side of the Moon.[17] The satellite did not gain speed, but its orbit was changed that allowed successful transmission of the photos.[18]
- Pioneer 10
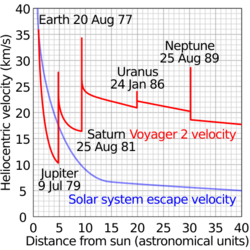
NASA's Pioneer 10 is a space probe launched in 1972 that completed the first mission to the planet Jupiter.[19] Thereafter, Pioneer 10 became the first of five artificial objects to achieve the escape velocity needed to leave the Solar System. In December 1973, Pioneer 10 spacecraft was the first one to use the gravitational slingshot effect to reach escape velocity to leave Solar System.[20][21]
- Pioneer 11
Pioneer 11 was launched by NASA in 1973, to study the asteroid belt, the environment around Jupiter and Saturn, solar winds, and cosmic rays.[19] It was the first probe to encounter Saturn, the second to fly through the asteroid belt, and the second to fly by Jupiter. To get to Saturn, the spacecraft got a gravity assist on Jupiter.[22][23][24]
- Mariner 10
The Mariner 10 probe was the first spacecraft to use the gravitational slingshot effect to reach another planet, passing by Venus on 5 February 1974 on its way to becoming the first spacecraft to explore Mercury.[25]
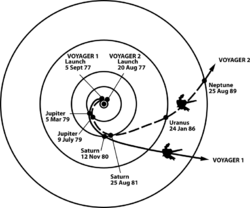
- Voyager 1
Voyager 1 was launched by NASA on September 5, 1977. It gained the energy to escape the Sun's gravity by performing slingshot maneuvers around Jupiter and Saturn.[26] Having operated for 48 years, 1 month and 21 days as of October 26, 2025 UTC [refresh], the spacecraft still communicates with the Deep Space Network to receive routine commands and to transmit data to Earth. Real-time distance and velocity data is provided[27] by NASA and JPL. At a distance of 152.2 astronomical unit|AU (22.8 billion km; 14.1 billion mi) from Earth as of January 12, 2020,[28] it is the most distant human-made object from Earth.[29]
- Voyager 2
Voyager 2 was launched by NASA on August 20, 1977, to study the outer planets. Its trajectory took longer to reach Jupiter and Saturn than its twin spacecraft but enabled further encounters with Uranus and Neptune.[30]
- Galileo
The Galileo spacecraft was launched by NASA in 1989 and on its route to Jupiter got three gravity assists, one from Venus (February 10, 1990), and two from Earth (December 8, 1990 and December 8, 1992). Spacecraft reached Jupiter in December 1995. Gravity assists also allowed Galileo to flyby two asteroids, 243 Ida and 951 Gaspra.[31][32]
- Ulysses
In 1990, NASA launched the ESA spacecraft Ulysses to study the polar regions of the Sun. All the planets orbit approximately in a plane aligned with the equator of the Sun. Thus, to enter an orbit passing over the poles of the Sun, the spacecraft would have to eliminate the speed it inherited from the Earth's orbit around the Sun and gain the speed needed to orbit the Sun in the pole-to-pole plane. It was achieved by a gravity assist from Jupiter on February 8, 1992.[33][34]
- MESSENGER
The MESSENGER mission (launched in August 2004) made extensive use of gravity assists to slow its speed before orbiting Mercury. The MESSENGER mission included one flyby of Earth, two flybys of Venus, and three flybys of Mercury before finally arriving at Mercury in March 2011 with a velocity low enough to permit orbit insertion with available fuel. Although the flybys were primarily orbital maneuvers, each provided an opportunity for significant scientific observations.[35][36]
- Cassini
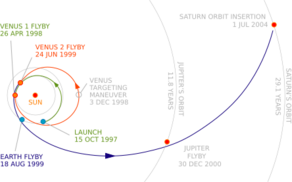
The Cassini–Huygens spacecraft was launched from Earth on 15 October 1997, followed by gravity assist flybys of Venus (26 April 1998 and 21 June 1999), Earth (18 August 1999), and Jupiter (30 December 2000). Transit to Saturn took 6.7 years, the spacecraft arrived at 1 July 2004.[37][38] Its trajectory was called "the Most Complex Gravity-Assist Trajectory Flown to Date" in 2019.[39]
After entering orbit around Saturn, the Cassini spacecraft used multiple Titan gravity assists to achieve significant changes in the inclination of its orbit as well so that instead of staying nearly in the equatorial plane, the spacecraft's flight path was inclined well out of the plane of the rings.[40] A typical Titan encounter changed the spacecraft's velocity by 0.75 km/s, and the spacecraft made 127 Titan encounters. These encounters enabled an orbital tour with a wide range of periapsis and apoapsis distances, various alignments of the orbit with respect to the Sun, and orbital inclinations from 0° to 74°. The multiple flybys of Titan also allowed Cassini to flyby other moons, such as Rhea and Enceladus.[citation needed]
- Rosetta
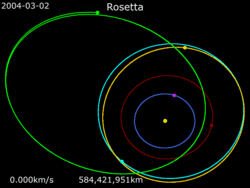
Rosetta · 67P/C-G · Earth · Mars · 21 Lutetia · 2867 Šteins
The Rosetta probe, launched in March 2004, used four gravity assist maneuvers (including one just 250 km from the surface of Mars, and three assists from Earth) to accelerate throughout the inner Solar System. That enabled it to flyby the asteroids 21 Lutetia and 2867 Šteins as well as eventually match the velocity of the 67P/Churyumov–Gerasimenko comet at the rendezvous point in August 2014.[41][42]
- New Horizons
New Horizons was launched by NASA in 2006, and reached Pluto in 2015. In 2007 it performed a gravity assist on Jupiter.[43][44]
- Juno
The Juno spacecraft was launched on August 5, 2011 (UTC). The trajectory used a gravity assist speed boost from Earth, accomplished by an Earth flyby in October 2013, two years after its launch on August 5, 2011.[45] In that way Juno changed its orbit (and speed) toward its final goal, Jupiter, after only five years.
- Parker Solar Probe
The Parker Solar Probe, launched by NASA in 2018, has seven planned Venus gravity assists. Each gravity assist brings the Parker Solar Probe progressively closer to the Sun. As of 2022, the spacecraft has performed five of its seven assists. The Parker Solar Probe's mission will make the closest approach to the Sun by any space mission.[46][47][48]
- Solar Orbiter
Solar Orbiter was launched by ESA in 2020. In its initial cruise phase, which lasts until November 2021, Solar Orbiter performed two gravity-assist manoeuvres around Venus and one around Earth to alter the spacecraft's trajectory, guiding it towards the innermost regions of the Solar System. The first close solar pass will take place on 26 March 2022 at around a third of Earth's distance from the Sun.[49]
- BepiColombo
BepiColombo is a joint mission of the European Space Agency (ESA) and the Japan Aerospace Exploration Agency (JAXA) to the planet Mercury. It was launched on 20 October 2018. It will use the gravity assist technique with Earth once, with Venus twice, and six times with Mercury. It will arrive in 2025. BepiColombo is named after Giuseppe (Bepi) Colombo who was a pioneer thinker with this way of maneuvers.[50]
- Lucy
Lucy was launched by NASA on 16 October 2021. It gained one gravity assist from Earth on the 16th of October, 2022,[51] and after a flyby of the main-belt asteroid 152830 Dinkinesh it will gain another in 2024.[52] In 2025, it will fly by the inner main-belt asteroid 52246 Donaldjohanson.[53] In 2027, it will arrive at the L4 Trojan cloud (the Greek camp of asteroids that orbits about 60° ahead of Jupiter), where it will fly by four Trojans, 3548 Eurybates (with its satellite), 15094 Polymele, 11351 Leucus, and 21900 Orus.[54] After these flybys, Lucy will return to Earth in 2031 for another gravity assist toward the L5 Trojan cloud (the Trojan camp which trails about 60° behind Jupiter), where it will visit the binary Trojan 617 Patroclus with its satellite Menoetius in 2033.
See also
- 3753 Cruithne, an asteroid which periodically has gravitational slingshot encounters with Earth
- Delta-v budget
- Low-energy transfer, a type of gravitational assist where a spacecraft is gravitationally snagged into orbit by a celestial body. This method is usually executed in the Earth-Moon system.
- Dynamical friction
- Flyby anomaly, an anomalous delta-v increase during gravity assists
- Gravitational keyhole
- Interplanetary Transport Network
- n-body problem
- Oberth effect, applying thrust near closest approach in a gravity well
- Pioneer H, first Out-Of-The-Ecliptic mission (OOE) proposed, for Jupiter and solar (Sun) observations
- STEREO, a gravity-assisted mission which used Earth's Moon to eject two spacecraft from Earth's orbit into heliocentric orbit
Notes
- ↑ In 1938, when Kondratyuk submitted his manuscript "To whoever will read in order to build" for publication, he dated the manuscript 1918–1919, although it was apparent that the manuscript had been revised at various times. See page 49 of NASA Technical Translation F-9285 (1 November 1965).
References
- ↑ 1.0 1.1 "Section 1: Environment, Chapter 4: Trajectories". NASA. https://solarsystem.nasa.gov/basics/chapter4-1.
- ↑ 2.0 2.1 2.2 "Gravity assist". The Planetary Society. http://www.planetary.org/blogs/guest-blogs/2013/20130926-gravity-assist.html.
- ↑ "Let gravity assist you ...". https://www.esa.int/Science_Exploration/Space_Science/Exploring_space/Let_gravity_assist_you.
- ↑ "A Gravity Assist Primer". NASA. https://solarsystem.nasa.gov/basics/primer/.
- ↑ Johnson, R. C. (January 2003). The Slingshot Effect (Report). Durham University. http://maths.dur.ac.uk/~dma0rcj/Psling/sling.pdf. Retrieved 2018-07-21.
- ↑ Kondratyuk's paper is included in the book: Mel'kumov, T. M., ed., Pionery Raketnoy Tekhniki [Pioneers of Rocketry: Selected Papers] (Moscow, U.S.S.R.: Institute for the History of Natural Science and Technology, Academy of Sciences of the USSR, 1964). An English translation of Kondratyuk's paper was made by NASA. See: NASA Technical Translation F-9285, pages 15–56 (1 November 1965).
- ↑ 7.0 7.1 7.2 Negri, Rodolfo Batista; Prado, Antônio Fernando Bertachini de Alme (14 July 2020). "A historical review of the theory of gravity-assists in the pre-spaceflight era". Journal of the Brazilian Society of Mechanical Sciences and Engineering 42 (8). doi:10.1007/s40430-020-02489-x. http://urlib.net/8JMKD3MGP3W34R/42T4NAH.
- ↑ Zander's 1925 paper, "Problems of Flight by Jet Propulsion: Interplanetary Flights" was translated by NASA. See NASA Technical Translation F-147 (1964); specifically, Section 7: Flight Around a Planet's Satellite for Accelerating or Decelerating Spaceship, pages 290–292.
- ↑ Eneev, T.; Akim, E.. "Mstislav Keldysh. Mechanics of the Space Flight" (in ru). Keldysh Institute of Applied Mathematics. http://www.keldysh.ru/events/fly.
- ↑ Egorov, Vsevolod Alexandrovich (September 1957). "Specific problems of a flight to the moon". Physics-Uspekhi 63 (9): 73–117. doi:10.3367/UFNr.0063.195709f.0073.
- ↑ Rauschenbakh, Boris V.; Ovchinnikov, Michael Yu.; McKenna-Lawlor, Susan M. P. (2003). Essential Spaceflight Dynamics and Magnetospherics. Dordrecht, Netherlands: Kluwer Academic. pp. 146–147. ISBN 0-306-48027-1. https://books.google.com/books?id=s8FRVu0blhgC&pg=PA146.
- ↑ Berger, Eric. "All Hail Luna 3, Rightful King of 1950s Space Missions". https://arstechnica.com/science/2019/10/all-hail-luna-3-rightful-king-of-1950s-space-missions/.
- ↑ "The Maths That Made Voyager Possible". 22 October 2012. https://www.bbc.com/news/science-environment-20033940.
- ↑ Portree, David S. F.. "The Challenge of the Planets, Part Three: Gravity". Wired. https://www.wired.com/2015/01/challenge-planets-part-three-gravity/. Retrieved 5 December 2022.
- ↑ Flandro, Gary. "Fast Reconnaissance Missions to the Outer Solar System Using Energy Derived from the Gravitational Field of Jupiter". http://www.gravityassist.com/IAF3-2/Ref.%203-143.pdf.
- ↑ Everitt, C. W. F. (June 2011). "Gravity Probe B: Final Results of a Space Experiment to Test General Relativity". Physical Review Letters 106 (22): 221101. doi:10.1103/PhysRevLett.106.221101. PMID 21702590. Bibcode: 2011PhRvL.106v1101E.
- ↑ Negri, Rodolfo Batista; Prado, Antônio Fernando Bertachini de Almeida (14 July 2020). "A historical review of the theory of gravity-assists in the pre-spaceflight era". Journal of the Brazilian Society of Mechanical Sciences and Engineering 42 (8): 406. doi:10.1007/s40430-020-02489-x. http://urlib.net/8JMKD3MGP3W34R/42T4NAH.
- ↑ Santos, Ignacio (2020). Simulation and Study of Gravity Assist Maneuvers (Report). http://www.diva-portal.org/smash/record.jsf?pid=diva2%3A1440099&dswid=4630.
- ↑ 19.0 19.1 Fimmel, R. O.; W. Swindell; E. Burgess (1974). SP-349/396 PIONEER ODYSSEY. NASA-Ames Research Center. SP-349/396. https://history.nasa.gov/SP-349/ch8.htm. Retrieved January 9, 2011.
- ↑ "Let Gravity Assist You..." (in en). https://www.sciencedaily.com/releases/2003/10/031023071115.htm.
- ↑ T. Franc (2011). "The Gravitational Assist". 20th Annual Conference of Doctoral Students, WDS'11 "Week of Doctoral Students 2011", Charles University, Faculty of Mathematics and Physics, Prague, Czech Republic, May 31, 2011 to June 3, 2011 : [proceedings of contributed papers]. Pt. 3 Physics (Vyd. 1 ed.). Praha: Matfyzpress. ISBN 978-80-7378-186-6. https://www.mff.cuni.cz/veda/konference/wds/proc/pdf11/WDS11_309_f12_Franc.pdf. Retrieved 5 December 2022.
- ↑ "Pioneer 11: In Depth". https://solarsystem.nasa.gov/missions/pioneer-11/in-depth/.
- ↑ Mars, Kelli (2 December 2019). "45 Years Ago, Pioneer 11 Explores Jupiter". https://www.nasa.gov/feature/45-years-ago-pioneer-11-explores-jupiter.
- ↑ "Pioneer 10 and 11, outer solar system explorers" (in en). https://www.planetary.org/space-missions/pioneer.
- ↑ "In Depth | Mariner 10". https://solarsystem.nasa.gov/missions/mariner-10/in-depth/.
- ↑ "A Gravity Assist Primer". NASA. https://solarsystem.nasa.gov/basics/primer/.
- ↑ "Voyager - Mission Status". https://voyager.jpl.nasa.gov/mission/status/.
- ↑ "Voyager – Mission Status". Jet Propulsion Laboratory. National Aeronautics and Space Administration. https://voyager.jpl.nasa.gov/mission/status/.,
- ↑ "Voyager 1". BBC Solar System. http://www.bbc.co.uk/science/space/solarsystem/space_missions/voyager_1.
- ↑ Butrica, Andrew. From Engineering Science to Big Science. p. 267. https://history.nasa.gov/SP-4219/Chapter11.html. Retrieved September 4, 2015. "Despite the name change, Voyager remained in many ways the Grand Tour concept, though certainly not the Grand Tour (TOPS) spacecraft. Voyager 2 was launched on August 20, 1977, followed by Voyager 1 on September 5, 1977. The decision to reverse the order of launch had to do with keeping open the possibility of carrying out the Grand Tour mission to Uranus, Neptune, and beyond. Voyager 2, if boosted by the maximum performance from the Titan-Centaur, could just barely catch the old Grand Tour trajectory and encounter Uranus. Two weeks later, Voyager 1 would leave on an easier and much faster trajectory, visiting Jupiter and Saturn only. Voyager 1 would arrive at Jupiter four months ahead of Voyager 2, then arrive at Saturn nine months earlier. Hence, the second spacecraft launched was Voyager 1, not Voyager 2. The two Voyagers would arrive at Saturn nine months apart, so that if Voyager 1 failed to achieve its Saturn objectives, for whatever reason, Voyager 2 still could be retargeted to achieve them, though at the expense of any subsequent Uranus or Neptune encounter."
- ↑ D'Amario, Louis A.; Bright, Larry E.; Wolf, Aron A. (May 1992). "Galileo trajectory design". Space Science Reviews 60 (1–4): 23. doi:10.1007/BF00216849. Bibcode: 1992SSRv...60...23D.
- ↑ "Galileo Heads Towards Second Gravity Assist". https://www.jpl.nasa.gov/news/galileo-heads-towards-second-gravity-assist.
- ↑ "ESA Science & Technology - Orbit of Ulysses". https://sci.esa.int/web/ulysses/-/42904-orbit-of-ulysses.
- ↑ "ESA Science & Technology - Gravity Assist". https://sci.esa.int/web/ulysses/-/33640-gravity-assist.
- ↑ "MESSENGER - Unlocking the Mysteries of Planet Mercury". https://messenger.jhuapl.edu/About/Mission-Design.html#gravity-assists.
- ↑ "Resources / News Archives FLYBY INFORMATION". https://messenger.jhuapl.edu/Resources/Flyby-Information.html.
- ↑ "Cassini Trajectory". https://solarsystem.nasa.gov/resources/11776/cassini-trajectory/.
 This article incorporates text from this source, which is in the public domain.
This article incorporates text from this source, which is in the public domain.
- ↑ "ESA Science & Technology - Getting to Saturn". https://sci.esa.int/web/cassini-huygens/-/31240-getting-to-saturn.
- ↑ Bellerose, Julie; Roth, Duane; Tarzi, Zahi; Wagner, Sean (2019). "The Cassini Mission: Reconstructing Thirteen Years of the Most Complex Gravity-Assist Trajectory Flown to Date" (in en). Space Operations: Inspiring Humankind's Future. Springer International Publishing. pp. 575–588. doi:10.1007/978-3-030-11536-4_22. ISBN 978-3-030-11535-7. https://link.springer.com/chapter/10.1007/978-3-030-11536-4_22. Retrieved 5 December 2022.
- ↑ "Gravity Assists | Mission". https://solarsystem.nasa.gov/missions/cassini/mission/gravity-assists/.
 This article incorporates text from this source, which is in the public domain.
This article incorporates text from this source, which is in the public domain.
- ↑ "ESA Science & Technology - Rosetta Second Earth Swing-by". https://sci.esa.int/web/rosetta/-/41758-rosetta-second-earth-swing-by.
- ↑ Alexander, C.; Holmes, D.; Goldstein, R.; Parker, J. (2 March 2008). "The U.S. Rosetta Project: Mars Gravity Assist". 2008 IEEE Aerospace Conference. pp. 1–9. doi:10.1109/AERO.2008.4526265. ISBN 978-1-4244-1487-1. https://trs.jpl.nasa.gov/handle/2014/41429.
- ↑ Boen, Brooke. "NASA - Grand Theft Pluto: New Horizons Gets a Boost From Jupiter Flyby" (in en). https://www.nasa.gov/mission_pages/newhorizons/news/jupiter_flyby.html.
- ↑ "New Horizons Jupiter Flyby" (in en). https://pds-atmospheres.nmsu.edu/data_and_services/atmospheres_data/Horizons/newhorizons.html.
- ↑ "NASA's Shuttle and Rocket Launch Schedule". NASA. http://www.nasa.gov/missions/highlights/schedule.html.
- ↑ "Parker Solar Probe Completes Its Fifth Venus Flyby – Parker Solar Probe". 19 October 2021. https://blogs.nasa.gov/parkersolarprobe/2021/10/19/parker-solar-probe-completes-its-fifth-venus-flyby/.
 This article incorporates text from this source, which is in the public domain.
This article incorporates text from this source, which is in the public domain.
- ↑ Garner, Rob (4 October 2018). "Parker Solar Probe Changed the Game Before It Even Launched". NASA. https://www.nasa.gov/feature/goddard/2018/parker-solar-probe-changed-the-game-before-it-even-launched.
- ↑ Guo, Yanping; Thompson, Paul; Wirzburger, John; Pinkine, Nick; Bushman, Stewart; Goodson, Troy; Haw, Rob; Hudson, James et al. (1 February 2021). "Execution of Parker Solar Probe's unprecedented flight to the Sun and early results" (in en). Acta Astronautica 179: 425–438. doi:10.1016/j.actaastro.2020.11.007. ISSN 0094-5765. Bibcode: 2021AcAau.179..425G.
- ↑ "GMS: Solar Orbiter's Orbit". 27 January 2020. https://svs.gsfc.nasa.gov/13532.
 This article incorporates text from this source, which is in the public domain.
This article incorporates text from this source, which is in the public domain.
- ↑ "ESA Science & Technology BepiColombo". 28 June 2022. https://sci.esa.int/web/bepicolombo/-/47346-fact-sheet.
- ↑ Lee Kanayama (16 October 2022). "Lucy completes its first Earth gravity assist after a year in space". NASA Spaceflight.com. https://www.nasaspaceflight.com/2022/10/lucy-first-earth-flyby.
- ↑ "NASA Awards Launch Services Contract for Lucy Mission". NASA. 31 January 2019. https://www.nasa.gov/press-release/nasa-awards-launch-services-contract-for-lucy-mission.
 This article incorporates text from this source, which is in the public domain.
This article incorporates text from this source, which is in the public domain.
- ↑ Dreier, Casey; Lakdawalla, Emily (30 September 2015). "NASA announces five Discovery proposals selected for further study". The Planetary Society. http://www.planetary.org/blogs/casey-dreier/2015/09301336-discovery-downselect.html.
- ↑ Chang, Kenneth (6 January 2017). "A Metal Ball the Size of Massachusetts That NASA Wants to Explore". The New York Times. https://www.nytimes.com/2017/01/06/science/nasa-psyche-asteroid.html.
External links
- Basics of Space Flight: A Gravity Assist Primer at NASA.gov
- Spaceflight and Spacecraft: Gravity Assist, discussion at Phy6.org
- "Gravitational Slingshot". MathPages.com. http://www.mathpages.com/home/kmath114/kmath114.htm.
- Double-ball drop experiment
 |