Astronomy:Eclipse cycle
Eclipses may occur repeatedly, separated by certain intervals of time: these intervals are called eclipse cycles.[1] The series of eclipses separated by a repeat of one of these intervals is called an eclipse series.
Eclipse conditions
Eclipses may occur when Earth and the Moon are aligned with the Sun, and the shadow of one body projected by the Sun falls on the other. So at new moon, when the Moon is in conjunction with the Sun, the Moon may pass in front of the Sun as viewed from a narrow region on the surface of Earth and cause a solar eclipse. At full moon, when the Moon is in opposition to the Sun, the Moon may pass through the shadow of Earth, and a lunar eclipse is visible from the night half of Earth. The conjunction and opposition of the Moon together have a special name: syzygy (Greek for "junction"), because of the importance of these lunar phases.
An eclipse does not occur at every new or full moon, because the plane of the Moon's orbit around Earth is tilted with respect to the plane of Earth's orbit around the Sun (the ecliptic): so as viewed from Earth, when the Moon appears nearest the Sun (at new moon) or furthest from it (at full moon), the three bodies are usually not exactly on the same line.
This inclination is on average about 5° 9′, much larger than the apparent mean diameter of the Sun (32′ 2″), the Moon as viewed from Earth's surface directly below the Moon (31′ 37″), and Earth's shadow at the mean lunar distance (1° 23′).
Therefore, at most new moons, Earth passes too far north or south of the lunar shadow, and at most full moons, the Moon misses Earth's shadow. Also, at most solar eclipses, the apparent angular diameter of the Moon is insufficient to fully occlude the solar disc, unless the Moon is around its perigee, i.e. nearer Earth and apparently larger than average. In any case, the alignment must be almost perfect to cause an eclipse.
An eclipse can occur only when the Moon is on or near the plane of Earth's orbit, i.e. when its ecliptic latitude is low. This happens when the Moon is around either of the two orbital nodes on the ecliptic at the time of the syzygy. Of course, to produce an eclipse, the Sun must also be around a node at that time – the same node for a solar eclipse or the opposite node for a lunar eclipse.
Recurrence
Up to three eclipses may occur during an eclipse season, a one- or two-month period that happens twice a year, around the time when the Sun is near the nodes of the Moon's orbit.
An eclipse does not occur every month, because one month after an eclipse the relative geometry of the Sun, Moon, and Earth has changed.
As seen from the Earth, the time it takes for the Moon to return to a node, the draconic month, is less than the time it takes for the Moon to return to the same ecliptic longitude as the Sun: the synodic month. The main reason is that during the time that the Moon has completed an orbit around the Earth, the Earth (and Moon) have completed about 1⁄13 of their orbit around the Sun: the Moon has to make up for this in order to come again into conjunction or opposition with the Sun. Secondly, the orbital nodes of the Moon precess westward in ecliptic longitude, completing a full circle in about 18.60 years, so a draconic month is shorter than a sidereal month. In all, the difference in period between synodic and draconic month is nearly 2 1⁄3 days. Likewise, as seen from the Earth, the Sun passes both nodes as it moves along its ecliptic path. The period for the Sun to return to a node is called the eclipse or draconic year: about 346.6201 days, which is about 1⁄20 year shorter than a sidereal year because of the precession of the nodes.
If a solar eclipse occurs at one new moon, which must be close to a node, then at the next full moon the Moon is already more than a day past its opposite node, and may or may not miss the Earth's shadow. By the next new moon it is even further ahead of the node, so it is less likely that there will be a solar eclipse somewhere on Earth. By the next month, there will certainly be no event.
However, about 5 or 6 lunations later the new moon will fall close to the opposite node. In that time (half an eclipse year) the Sun will have moved to the opposite node too, so the circumstances will again be suitable for one or more eclipses.
Periodicity
The periodicity of solar eclipses is the interval between any two solar eclipses in succession, which will be either 1, 5, or 6 synodic months.[2] It is calculated that the earth will experience a total number of 11,898 solar eclipses between 2000 BCE and 3000 CE. A particular solar eclipse will be repeated approximately after every 18 years 11 days and 8 hours (6,585.32 days) of period, but not in the same geographical region.[3] A particular geographical region will experience a particular solar eclipse in every 54 years 34 days period.[2] Total solar eclipses are rare events, although they occur somewhere on Earth every 18 months on average,[4]
Repetition of solar eclipses
For the repetition of a solar eclipse, the geometric alignment of the Earth, Moon and Sun, as well as some parameters of the lunar orbit should be repeated. The following parameters and criteria must be repeated for the repetition of a solar eclipse:
- The Moon must be in new phase.
- The longitude of perigee or apogee of the Moon must be the same.
- The longitude of the ascending node or descending node must be the same.
- The Earth will be nearly the same distance from the Sun, and tilted to it in nearly the same orientation.
These conditions are related with the three periods of the Moon's orbital motion, viz. the synodic month, anomalistic month and draconic month. In other words, a particular eclipse will be repeated only if the Moon will complete roughly an integer number of synodic, draconic, and anomalistic periods (223, 242, and 239) and the Earth-Sun-Moon geometry will be nearly identical to that eclipse. The Moon will be at the same node and the same distance from the Earth. Gamma (how far the moon is north or south of the ecliptic during an eclipse) changes monotonically throughout any single Saros series. The change in gamma is larger when Earth is near its aphelion (June to July) than when it is near perihelion (December to January). When the Earth is near its average distance (March to April or September to October), the change in gamma is average.
Repetition of lunar eclipses
For the repetition of a lunar eclipse, the geometric alignment of the Moon, Earth and Sun, as well as some parameters of the lunar orbit should be repeated. The following parameters and criteria must be repeated for the repetition of a lunar eclipse:
- The Moon must be in full phase.
- The longitude of perigee or apogee of the Moon must be the same.
- The longitude of the ascending node or descending node must be the same.
- The Earth will be nearly the same distance from the Sun, and tilted to it in nearly the same orientation.
These conditions are related with the three periods of the Moon's orbital motion, viz. the synodic month, anomalistic month and draconic month. In other words, a particular eclipse will be repeated only if the Moon will complete roughly an integer number of synodic, draconic, and anomalistic periods (223, 242, and 239) and the Earth-Sun-Moon geometry will be nearly identical to that eclipse. The Moon will be at the same node and the same distance from the Earth. Gamma changes monotonically throughout any single Saros series. The change in gamma is larger when Earth is near its aphelion (June to July) than when it is near perihelion (December to January). When the Earth is near its average distance (March to April or September to October), the change in gamma is average.
Eclipses would not occur in every month
Another thing to consider is that the motion of the Moon is not a perfect circle. Its orbit is distinctly elliptic, so the lunar distance from Earth varies throughout the lunar cycle. This varying distance changes the apparent diameter of the Moon, and therefore influences the chances, duration, and type (partial, annular, total, mixed) of an eclipse. This orbital period is called the anomalistic month, and together with the synodic month causes the so-called "full moon cycle" of about 14 lunations in the timings and appearances of full (and new) Moons. The Moon moves faster when it is closer to the Earth (near perigee) and slower when it is near apogee (furthest distance), thus periodically changing the timing of syzygies by up to 14 hours either side (relative to their mean timing), and causing the apparent lunar angular diameter to increase or decrease by about 6%. An eclipse cycle must comprise close to an integer number of anomalistic months in order to perform well in predicting eclipses.
If the Earth had a perfectly circular orbit centered around the Sun, and the Moon's orbit was also perfectly circular and centered around the Earth, and both orbits were coplanar (on the same plane) with each other, then two eclipses would happen every lunar month (29.53 days). A lunar eclipse would occur at every full moon, a solar eclipse every new moon, and all solar eclipses would be the same type. In fact the distances between the Earth and Moon and that of the Earth and the Sun vary because both the Earth and the Moon have elliptic orbits. Also, both the orbits are not on the same plane. The Moon's orbit is inclined about 5.14° to Earth's orbit around the Sun. So the Moon's orbit crosses the ecliptic at two points or nodes. If a New Moon takes place within about 17° of a node, then a solar eclipse will be visible from some location on Earth.[5][6][7]
At an average angular velocity of 0.99° per day, the Sun takes 34.5 days to cross the 34° wide eclipse zone centered on each node. Because the Moon's orbit with respect to the Sun has a mean duration of 29.53 days, there will always be one and possibly two solar eclipses during each 34.5-day interval when the Sun passes through the nodal eclipse zones. These time periods are called eclipse seasons.[2] Either two or three eclipses happen each eclipse season. During the eclipse season, the inclination of the Moon's orbit is low, hence the Sun, Moon, and Earth become aligned straight enough (in syzygy) for an eclipse to occur.
Numerical values
These are the lengths of the various types of months as discussed above (according to the lunar ephemeris ELP2000-85, valid for the epoch J2000.0; taken from (e.g.) Meeus (1991) ):
- SM = 29.530588853 days (Synodic month)[8]
- DM = 27.212220817 days (Draconic month)[9]
- AM = 27.55454988 days (Anomalistic month)[10]
- EY = 346.620076 days (Eclipse year)
Note that there are three main moving points: the Sun, the Moon, and the (ascending) node; and that there are three main periods, when each of the three possible pairs of moving points meet one another: the synodic month when the Moon returns to the Sun, the draconic month when the Moon returns to the node, and the eclipse year when the Sun returns to the node. These three 2-way relations are not independent (i.e. both the synodic month and eclipse year are dependent on the apparent motion of the Sun, both the draconic month and eclipse year are dependent on the motion of the nodes), and indeed the eclipse year can be described as the beat period of the synodic and draconic months (i.e. the period of the difference between the synodic and draconic months); in formula:
- [math]\displaystyle{ \mbox{EY} = \frac{\mbox{SM} \times \mbox{DM}}{\mbox{SM}-\mbox{DM}} }[/math]
as can be checked by filling in the numerical values listed above.
Eclipse cycles have a period in which a certain number of synodic months closely equals an integer or half-integer number of draconic months: one such period after an eclipse, a syzygy (new moon or full moon) takes place again near a node of the Moon's orbit on the ecliptic, and an eclipse can occur again. However, the synodic and draconic months are incommensurate: their ratio is not an integer number. We need to approximate this ratio by common fractions: the numerators and denominators then give the multiples of the two periods – draconic and synodic months – that (approximately) span the same amount of time, representing an eclipse cycle.
These fractions can be found by the method of continued fractions: this arithmetical technique provides a series of progressively better approximations of any real numeric value by proper fractions.
Since there may be an eclipse every half draconic month, we need to find approximations for the number of half draconic months per synodic month: so the target ratio to approximate is: SM / (DM/2) = 29.530588853 / (27.212220817/2) = 2.170391682
The continued fractions expansion for this ratio is:
2.170391682 = [2;5,1,6,1,1,1,1,1,11,1,...]:[11] Quotients Convergents half DM/SM decimal named cycle (if any) 2; 2/1 = 2 synodic month 5 11/5 = 2.2 pentalunex 1 13/6 = 2.166666667 semester 6 89/41 = 2.170731707 hepton 1 102/47 = 2.170212766 octon 1 191/88 = 2.170454545 tzolkinex 1 293/135 = 2.170370370 tritos 1 484/223 = 2.170403587 saros 1 777/358 = 2.170391061 inex 1 8253/3803 = 2.170391556 Utting cycle 11 9031/4161 = 2.170391732 selebit 1 9808/4519 = 2.170391679 square year ...
The ratio of synodic months per half eclipse year yields the same series:
5.868831091 = [5;1,6,1,1,1,1,1,11,1,...]
Quotients Convergents
SM/half EY decimal SM/full EY named cycle
5; 5/1 = 5 pentalunex
1 6/1 = 6 12/1 semester
6 41/7 = 5.857142857 hepton
1 47/8 = 5.875 47/4 octon
1 88/15 = 5.866666667 tzolkinex
1 135/23 = 5.869565217 tritos
1 223/38 = 5.868421053 223/19 saros
1 358/61 = 5.868852459 716/61 inex
1 3803/648 = 5.868846931 Utting cycle
11 4161/709 = 5.868829337 selebit
1 4519/770 = 5.868831169 4519/385 square year
...
Each of these is an eclipse cycle. Less accurate cycles may be constructed by combinations of these.
Eclipse cycles
This table summarizes the characteristics of various eclipse cycles, and can be computed from the numerical results of the preceding paragraphs; cf. Meeus (1997) Ch.9. More details are given in the comments below, and several notable cycles have their own pages. Many other cycles have been noted, some of which have been named.[12]
Any eclipse cycle, and indeed the interval between any two eclipses, can be expressed as a combination of saros (s) and inex (i) intervals. These are listed in the column "formula".
| Cycle | Formula | Days | Synodic months |
Draconic months |
Anomalistic months |
Eclipse years |
Tropical years |
Eclipse seasons |
Node |
|---|---|---|---|---|---|---|---|---|---|
| fortnight | 19i − 30 1⁄2s | 14.77 | 0.5 | 0.543 | 0.536 | 0.043 | 0.040 | 0.086 | alternate |
| synodic month | 38i − 61s | 29.53 | 1 | 1.085 | 1.072 | 0.085 | 0.081 | 0.17 | same |
| pentalunex | 53s − 33i | 147.65 | 5 | 5.426 | 5.359 | 0.426 | 0.404 | 0.852 | alternate |
| semester | 5i − 8s | 177.18 | 6 | 6.511 | 6.430 | 0.511 | 0.485 | 1 | alternate |
| lunar year | 10i − 16s | 354.37 | 12 | 13.022 | 12.861 | 1.022 | 0.970 | 2 | same |
| hexon | 13s - 8i | 1,033.57 | 35 | 37.982 | 37.510 | 2.982 | 2.830 | 6 | same |
| hepton | 5s − 3i | 1,210.73 | 41 | 44.485 | 43.952 | 3.485 | 3.321 | 7 | alternate |
| octon | 2i − 3s | 1,387.94 | 47 | 51.004 | 50.371 | 4.004 | 3.800 | 8 | same |
| tzolkinex | 2s − i | 2,598.69 | 88 | 95.497 | 94.311 | 7.497 | 7.115 | 15 | alternate |
| Hibbardina[12] | 31s + 19i | 3,277.90 | 111 | 119.975 | 120.457 | 9.457 | 8.975 | 19 | alternate |
| sar (half saros) | 1⁄2s | 3,292.66 | 111.5 | 120.999 | 119.496 | 9.499 | 9.015 | 19 | same |
| tritos | i − s | 3,986.63 | 135 | 146.501 | 144.681 | 11.501 | 10.915 | 23 | alternate |
| saros (s) | s | 6,585.32 | 223 | 241.999 | 238.992 | 18.999 | 18.030 | 38 | same |
| Metonic cycle | 10i − 15s | 6,939.69 | 235 | 255.032 | 251.864 | 20.022 | 19.000 | 40 | same |
| semanex[12] | 3s - i | 9,184,01 | 311 | 336.144 | 333.303 | 26.496 | 25.145 | 53 | alternate |
| thix[12] | 4i - 5s | 9,361.20 | 317 | 342.629 | 339.733 | 27.007 | 25.145 | 54 | same |
| inex (i) | i | 10,571.95 | 358 | 388.500 | 383.674 | 30.500 | 28.945 | 61 | alternate |
| exeligmos | 3s | 19,755.96 | 669 | 725.996 | 716.976 | 56.996 | 54.090 | 114 | same |
| Aubrey cycle[12] | i + 1⁄2s | 20,449.93 | 692.5 | 751.498 | 742.162 | 58.996 | 55.990 | 118 | alternate |
| unidos[12] | i + 2s | 23,742.59 | 804 | 872.497 | 861.658 | 68.497 | 65.005 | 137 | alternate |
| Callippic cycle or 4 Metonic cycles | 40i − 60s | 27,758.76 | 940 | 1020.093 | 1007.420 | 80.085 | 76.000 | 160 | same |
| triad | 3i | 31,715.85 | 1074 | 1165.500 | 1151.021 | 91.500 | 86.835 | 183 | alternate |
| quarter Palmen cycle[12] | 4i - 1s | 35,702.48 | 1209 | 1417.266 | 1295.702 | 103.001 | 97.750 | 206 | same |
| Mercury cycle[12] | 2i + 3s | 40,899.864 | 1385 | 1502.996 | 1484.323 | 117.996 | 111.980 | 236 | same |
| tritrix[12] | 3i + 3s | 51,471.815 | 1743 | 1891.496 | 1867.997 | 148.496 | 140.925 | 297 | alternate |
| de la Hire cycle[12] | 6i | 63,431.703 | 2148 | 2331.000 | 2302.410 | 183.000 | 173.670 | 366 | same |
| trihex[12] | 3i + 6s | 71,227.778 | 2412 | 2167.492 | 2584.973 | 205.492 | 195.015 | 411 | alternate |
| Lambert II cycle[12] | 9i + s | 101,732.876 | 3445 | 3738.500 | 3692.054 | 293.500 | 278.535 | 587 | alternate |
| Macdonald cycle[12] | 6i + 7s | 109,528.951 | 3709 | 4024.991 | 3794.986 | 315.991 | 299.880 | 632 | same |
| Utting cycle[12] | 10i + s | 112,304.826 | 3803 | 4127.000 | 4075.727 | 324.000 | 307.480 | 648 | same |
| selebit | 11i + s | 122,876.78 | 4161 | 4515.500 | 4459.401 | 354.499 | 336.425 | 709 | alternate |
| Hipparchic cycle | 25i − 21s | 126,007.02 | 4267 | 4630.531 | 4573.002 | 363.531 | 344.996 | 727 | alternate |
| Square year | 12i + s | 133,448.73 | 4519 | 4904.000 | 4843.074 | 384.999 | 365.371 | 770 | same |
| Gregoriana[12] | 6i + 11s | 135,870.235 | 4601 | 4992.986 | 4930.955 | 391.986 | 372.000 | 784 | same |
| hexdodeka[12] | 6i + 12s | 142,455.556 | 4824 | 5234.985 | 5169.947 | 410.985 | 390.030 | 822 | same |
| Grattan Guinness cycle[12] | 12i - 4s | 142,809.923 | 4836 | 5248.007 | 5182.807 | 412.007 | 391.000 | 824 | same |
| Babylonian | 14i + 2s | 161,177.95 | 5458 | 5922.999 | 5849.413 | 464.999 | 441.291 | 930 | same |
| Basic period | 18i | 190,295.109 | 6444 | 6993.001 | 6906.123 | 549.001 | 521.011 | 1098 | same |
| Chalepe[12] | 18i + 2s | 203,465.751 | 6,890 | 7476.999 | 7,384.107 | 586.999 | 557.071 | 1174 | same |
| tetradia (Meeus III) | 22i − 4s | 206,241.63 | 6984 | 7579.008 | 7484.849 | 595.008 | 564.671 | 1190 | same |
| tetradia (Meeus I) | 19i + 2s | 214,037.70 | 7248 | 7865.500 | 7767.781 | 617.500 | 586.016 | 1235 | alternate |
| hyper exeligmos[12] | 24i + 12s | 332,750.665 | 11268 | 12227.987 | 12076.070 | 989.987 | 911.041 | 1920 | same |
| cartouche[12] | 52i | 549,741.426 | 18616 | 20202.006 | 19951.022 | 1586.006 | 1505.142 | 3172 | same |
| Palaea-Horologia[12] | 55i + 3s | 601,213.240 | 20359 | 22093.502 | 21819.0186 | 1734.502 | 1646.0673 | 3469 | alternate |
| hybridia[12] | 55i + 4s | 607,798.561 | 20582 | 22335.501 | 22058.0108 | 1753.501 | 1664.097 | 3507 | alternate |
| Selenid 1[12] | 55i + 5s | 614,383.883 | 20805 | 22577.499 | 22297.003 | 1772.499 | 1682.127 | 3545 | alternate |
| Proxima[12] | 58i + 5s | 646,099.734 | 21879 | 23743.000 | 23448.023 | 1864.000 | 1768.962 | 3728 | same |
| heliotrope[12] | 58i + 6s | 652,685.055 | 22102 | 25923.158 | 23687.0155 | 1882.998 | 1786.992 | 3766 | same |
| Megalosaros[12] | 58i + 7s | 659,270.376 | 22325 | 24226.997 | 23926.008 | 1901.997 | 1805.023 | 3804 | same |
| immobilis[12] | 58i + 8s | 665,855.697 | 22548 | 24468.996 | 24165.000 | 1920.996 | 1823.052 | 3842 | same |
| accuratissima[12] | 58i + 9s | 672,441.019 | 22771 | 24710.994 | 24403.992 | 1939.994 | 1841.083 | 3880 | alternate |
| Mackay cycle[12] | 76i + 9s | 1,076,773.829 | 29215 | 31703.996 | 31,310.115 | 2488.996 | 2362.093 | 4978 | alternate |
| Selenid 2[12] | 95i + 11s | 1,076,773.829 | 36463 | 39569.496 | 39077.896 | 3106.496 | 2948.109 | 6213 | alternate |
| Horologia[12] | 110i + 7s | 1,209,011.802 | 40941 | 44429.003 | 43877.029 | 3488.003 | 3310.164 | 6976 | same |
Notes
- Fortnight
- Half a synodic month (29.53 days). When there is an eclipse, there is a fair chance that at the next syzygy there will be another eclipse: the Sun and Moon will have moved about 15° with respect to the nodes (the Moon being opposite to where it was the previous time), but the luminaries may still be within bounds to make an eclipse. For example, penumbral lunar eclipse of May 26, 2002 is followed by the annular solar eclipse of June 10, 2002 and penumbral lunar eclipse of June 24, 2002. The shortest lunar fortnight between a new moon and a full moon lasts only about 13 days and 21.5 hours, while the longest such lunar fortnight lasts about 15 days and 14.5 hours. (Due to evection, these values are different going from quarter moon to quarter moon. The shortest lunar fortnight between first and last quarter moons lasts only about 13 days and 12 hours, while the longest lasts about 16 days and 2 hours.)
- For more information see eclipse season.
- Synodic month
- Similarly, two events one synodic month apart have the Sun and Moon at two positions on either side of the node, 29° apart: both may cause a partial eclipse. For a lunar eclipse, it is a penumbral lunar eclipse.
- Pentalunex
- 5 synodic months. Successive solar or lunar eclipses may occur 1, 5 or 6 synodic months apart.[13]
- Semester
- Half a lunar year. Eclipses will repeat exactly one semester apart at alternating nodes in a cycle that lasts for 8 eclipses. Because it is close to a half integer of anomalistic, draconic months, and tropical years, each solar eclipse will (usually) alternate between hemispheres each semester, as well as alternate between total and annular. Hence there is usually a maximum of one total or annular eclipse each in a given lunar year. (However, in the middle of an eight-semester series the hemispheres switch, and there is a switch during the series between whether the odd ones or the even ones are total.) For lunar eclipses, eclipses will repeat exactly one semester apart at alternating nodes in a cycle that lasts for 8 eclipses. Because it is close to a half integer of anomalistic, draconic months, and tropical years, each lunar eclipse will usually alternate between edges of Earth's shadow each semester, as well as alternate between Lunar eclipses with the moon’s penumbral and umbral shadow difference less or greater than 1. Hence there is usually a maximum of one Lunar eclipse with Moon’s penumbral and umbral shadow difference less or greater than 1 each in a given lunar year.
- Lunar year
- Twelve (synodic) months, a little longer than an eclipse year: the Sun has returned to the node, so eclipses may again occur:
- Hexon
- 6 eclipse seasons, and a fairly short eclipse cycle. Each eclipse in a hexon series (except the last) is followed by an eclipse whose saros series number is 8 lower, always occurring at the same node. It is equal to 35 synodic months, 1 less than 3 lunar years (36 synodic months). At any given time there are six hexon series active.
- Hepton
- 7 eclipse seasons, and one of the less noteworthy eclipse cycles. Each eclipse in a hepton is followed by an eclipse 3 saros series before, always occurring at alternating nodes. It is equal to 41 synodic months. The interval is nearly a whole number of weeks (172.96), so each eclipse is followed by another that is usually on the same day of the week (moving backwards irregularly by an average of a quarter day). At any given time there are seven hepton series active.
- Octon
- 8 eclipse seasons, 1⁄5 of the Metonic cycle, and a fairly decent short eclipse cycle, but poor in anomalistic returns. Each octon in a series is 2 saros apart, always occurring at the same node. It is equal to 47 synodic months. At any given time there are eight octon series active.
- Tzolkinex
- Includes a half draconic month, so occurs at alternating nodes and alternates between hemispheres. Each consecutive eclipse is a member of preceding saros series from the one before. Equal to nearly ten tzolk'ins. Every third tzolkinex in a series is near an integer number of anomalistic months and so will have similar properties.
- Hibbardina
- An eclipse cycle with a short life expectancy for a series (which is made up of 3 eclipses). The addition of 1 lunation creates another cycle that follows the same circumstances. Both cycles surround a sar (half-saros).[14]
- Sar (half saros)
- Includes an odd number of fortnights (223). As a result, eclipses alternate between lunar and solar with each cycle, occurring at the same node and with similar characteristics. A solar eclipse with small gamma will be followed by a very central total lunar eclipse. A solar eclipse where the moon's penumbra just barely grazes the southern limb of earth will be followed half a saros later by a lunar eclipse where the moon just grazes the southern limb of the earth's penumbra.[15]
- Tritos
- A mediocre cycle, equal to an inex minus a saros. A triple tritos is close to an integer number of anomalistic months and so will have similar properties.
- Saros
- The best known eclipse cycle, and one of the best for predicting eclipses, in which 223 synodic months equal 242 draconic months with an error of only 51 minutes. It is also very close to 239 anomalistic months, which makes the circumstances between two eclipses one saros apart very similar. Being a third of a day more than a whole number of days, each succeeding eclipse is centered about 120° further west over the earth.
- Metonic cycle or enneadecaeteris
- Defined as nearly 6940 days, this is just a few hours over 19 years of 365 1⁄4 days and is 235 synodic months, but is also 5 "octon" periods and close to 20 eclipse years: so it yields a short series of four or five eclipses on or near the same calendar date or on two calendar dates. It is equivalent to 110 "hollow months" of 29 days and 125 "full months" of 30 days.
- Semanex
- Very accurate in that an integer number of weeks are achieved. Each eclipse in this period is a member of a preceding saros series, always occurring on alternating nodes. It equals 25 years 1 month 14 days or 311 lunations.[12]
- Thix
- An eclipse cycle approximating 36 tzolk'ins. Each eclipse in this period is 4 saros series apart, always occurring on the same node. It equals 25 years 6 months 18 days or 317 lunations.[12]
- Inex
- Very convenient in the classification of eclipse cycles. One inex after an eclipse, another eclipse takes place at almost the same longitude, but at the opposite latitude. Inex series, after a sputtering beginning, go on for many thousands of years giving eclipses every 29 years minus 20 days. The inex cycle is the cycle that produces the highest number of eclipses while it lasts. Inex series 30 first produced a solar eclipse in saros series -245 (in 9435 BC), has been producing eclipses every 29 years since saros series -197 (in 8045 BC), and will continue long past AD 15,000,[16] by which time it will have produced 707 consecutive eclipses. The name was introduced by George van den Bergh in 1951.[12]
- Exeligmos
- A triple saros, with the advantage that it has nearly an integer number of days, so the next eclipse will be visible at locations near the eclipse that occurred one exeligmos earlier, in contrast to the saros, in which the eclipse occurs about 8 hours later in the day or about 120° to the west of the eclipse that occurred one saros earlier.
- Aubrey cycle
- Named for the calculation of eclipses measured with Aubrey holes, located at Stonehenge. With 1385 fortnights, eclipses alternate between lunar and solar in 56 years minus 3.5 days.[12]
- Unidos
- Very close to 65 years. Equals 67 lunar years and exceeds 65 Julian years by only 1.3 days. Name suggested by Karl Palmen in that 2 saros are added over an inex.[12]
- Callippic cycle
- 940 synodic months, equivalent to 441 hollow months and 499 full months; thus 4 Metonic cycles minus one day or precisely 76 years of 365 1⁄4 days. It equals 940 lunations with an error of only 5.9 hours. This cycle, though useful for example in the calculation of the date of Easter, can produce at most two solar eclipses (both partial) and at most two lunar eclipses (both penumbral). The Callipic cycle is 20 octons, and series of octons often produce only 21 eclipses, so only the first and the last of such a series are separated by a Callipic cycle. Most eclipses are not followed by another eclipse 940 lunations later, but rather 939 lunations later (two inex and a saros), which comes near an integer number of draconic months, producing similar eclipses.[12]
- Triad
- A triple inex, with the advantage that it has nearly an integer number of anomalistic months, which makes the circumstances between two eclipses one Triad apart very similar, but at the opposite latitude. Almost exactly 87 calendar years minus 2 months. The triad means that every third saros series will be similar (central eclipses mostly total or mostly annular for example). Saros 130, 133, 136, 139, 142 and 145, for example, all produce mainly total central eclipses.
- Quarter Palmen cycle
- Named after Karl Palmen in that a saros is subtracted from 4 inex. Each eclipse is followed by an eclipse 4 saros series later, always occurring at the same node. It equals 97 years 9 months or 1209 lunations.[12]
- Mercury cycle
- Equals approximately 353 synodic periods of Mercury,[17] so that eclipses synchronize with the timing of Mercury's position in its orbit during each period, equaling 112 years minus one week or 1385 lunations.[12]
- Tritrix
- Equals 3 inex plus 3 saros, which's 140 years 11 months or 1743 lunations, always occurring on alternating nodes.[12]
- de la Hire cycle
- A sextuple inex, adopted by Phillippe de la Hire in his Tabularum Astronomicarum in 1687. It equals 6 inex periods, which's 173 years 8 months 3 days or 2148 lunations, equaling 179 lunar years, always occurring on the same node at nearly an integer number of anomalistic months, as it equals 2 triads.[12]
- Trihex
- Equals 3 inex plus 6 saros, lasting 195 years 6 days or 2412 lunations, equaling 201 lunar years, always occurring at alternating nodes.[12]
- Lambert II cycle
- An eclipse cycle in which eclipses occur in similar circumstances, as nearly an integer number of anomalistic months are achieved. It equals 278 years 6 months 15 days or 3445 lunations.[12]
- Macdonald cycle
- An eclipse cycle equal to 299 years 11 months minus 12 days or 3709 lunations. It equals 299 years 10 months 18 days or 3709 lunations, always occurring on the same node.[12]
- Utting cycle
- The seventh convergent in the continued fractions development between the ratio of the eclipse year and synodic month. It equals 307 years 6 months minus 5 days or 3803 lunations, giving it a life expectancy of over 137,000 years for such series. First discussed by James Utting in 1827.[12]
- Selebit
- An eclipse cycle where the number of eclipse years (354.5) closely matches (by chance) the number of days in a lunar year (354.371). It equals approximately 336 years 5 months 6 days or 4161 lunations. It is a convergent in the continued fractions development of the ratio between the eclipse year and the synodic month, giving a series of eclipses one selebit apart a life expectancy of thousands of years.
- Hipparchic cycle
- Not a noteworthy eclipse cycle, but Hipparchus constructed it to closely match an integer number of synodic and anomalistic months, years (345), and days. By comparing his own eclipse observations with Babylonian records from 345 years earlier, he could verify the accuracy of the various periods that the Chaldeans used.
- Square year
- An eclipse cycle where the number of solar years (365.371) closely matches the number of days in 1 solar year (365.242). Lasting 365 years 4.5 months or 4519 lunations. It is the eighth convergent in the continued fractions development of the ratio between the eclipse year and the synodic month, giving a series of eclipses one square year apart a life expectancy of thousands of years. Many eclipses of our day belong to "square year" series or selebit series that have been going for over 13,000 years, and many will continue for over 13,000 years.[16] A square year series alone can total more than 5 million years from beginning to end.[12]
- Gregoriana
- Known for returning toward the same day of the week and Gregorian calendar as approximately an integer number of years, months, weeks, and days are achieved, as such period lasts 372 years or 4601 lunations, always occurring on the same node.[12][18]
- Hexdodeka
- Equals 6 inex plus 12 saros, marking 390 years plus 12 days or 4824 lunations, which is 402 lunar years, always occurring on the same node. It is useful for giving accurate calculations of the timing of lunisolar syzygies.[12]
- Grattan Guinness cycle
- The shortest cycle that calculates eclipses in both the Gregorian and lunar calendar. It equals 391 years or 4836 lunations, which is 403 lunar years. Discovered by Henry Grattan Guinness.[19][12]
- Babylonian
- The ratio 5923 returns to latitude in 5458 months was used by the Chaldeans in their astronomical computations.
- Basic period
- Achieves nearly an integer number of Calendar years (521 years plus 4 days), anomalistic years (521 years minus 5 days), and weeks, as it equals 6444 lunations, which is 537 lunar years, leading to eclipses on the same day of the Julian calendar and week. According to Lalande (Astronomie, 3rd ed., vol. II, 195) the basic period was first discovered by A.G. Pingré. It was also mentioned by A. Mackay and rediscovered by Monck (1902), Schrader (1913), and Alexander Pogo (1935). It was also mentioned by Torroja Menéndez (1941) and in Barlow et al. (1944) along with Van den Bergh.[12]
- Chalepe
- Equals 18 inex plus 2 saros, therefore 557 years 1 month minus 3 days or 6890 lunations at nearly an integer number of anomalistic months.[12]
- Tetradia
- Sometimes 4 total lunar eclipses occur in a row with intervals of 6 lunations (one semester) between them, and this is called a tetrad. Giovanni Schiaparelli noticed that there are eras when such tetrads occur comparatively frequently, interrupted by eras when they are rare. This variation takes about 6 centuries. Antonie Pannekoek (1951) offered an explanation for this phenomenon and found a period of 591 years. Van den Bergh (1954) from Theodor von Oppolzer's Canon der Finsternisse found a period of 586 years. This happens to be an eclipse cycle; see Meeus [I] (1997). The phenomenon is related to the elliptical orbit of the earth, as explained below. Recently Tudor Hughes explained that secular changes in the eccentricity of the Earth's orbit cause the period for occurrence of tetrads to be variable, and it is currently about 565 years; see Meeus III (2004) for a detailed discussion.
- Hyper exeligmos
- Equals 12 Callippic cycles minus 1 lunar year, so therefore 911 years plus 15 days or 11268 lunations, which is 939 lunar years. Although eclipses 939 lunations apart have similar character (as nearly an integer number of draconic months are achieved), 12 such periods shows significant changes.[12]
- Cartouche
- Equals 52 inex, therefore 1505 years 1 month 23 days or 18616 lunations. Eclipses in this period occur at a similar distance as nearly an integer number of anomalistic months are achieved.[12]
- Palaea-Horologia
- Equals 55 inex plus 3 saros, which is 1646 years 24 days or 20359 lunations. Useful for calculating the timing of eclipses.[12]
- hybridia
- Equals 55 inex plus 4 saros, therefore 1664 years 1 month 5 days or 20582 lunations, near an integer number of anomalistic months, therefore having similar properties, but at the opposite latitude.[12]
- Selenid
- The name for eclipse cycles useful for calculating the magnitudes of eclipses in the 3rd millennium A.D. George van den Bergh first mentioned a period of 55 inex plus 5 saros (1682 years 1 month 17 days or 20805 lunations) before mentioning a period of 95 inex plus 11 saros (2948 years 1 month 9 days or 36463 lunations) in 1951.[12]
- Proxima
- Equals 58 inex plus 5 saros and is nearly 2485 tzolkins, therefore 1769 years minus 15 days or 21879 lunations, always occurring at the same node and toward an integer number of draconic and anomalistic months and weeks, making the circumstances of each eclipse a proxima apart similar such as character and weekly returns.[12]
- Heliotrope
- Equals 58 inex plus 6 saros, therefore 1787 years minus 3 days or 22102 lunations, making it useful for calculating the longitudinal positions of the central lines of eclipses on Earth's surface near an integer number of years.[12]
- Megalosaros
- Equals 58 inex plus 7 saros, which is 95 Metonic cycles, therefore 1805 years plus 8 days or 22325 lunations, always occurring on the same node, and revealing the Metonic cycle's mismatch from 19 years as 95 repeats significantly accumulates the mismatch. It is a relatively close approximation to a period of eclipses 100 saros cycles apart (exceeding that value by only 25 lunations), as 100 saros cycles exceeds the life expectancy of a saros series.[12][20]
- Immobilis
- Equals 58 inex plus 8 saros, which is 1879 lunar years, therefore 1823 years plus 19 days or 22548 lunations, always occurring on the same node.[12]
- Accuratissima
- Equals 58 inex plus 9 saros, therefore 1841 years 1 month or 22771 lunations, which's approximately an integer number of weeks, allowing eclipses to occur toward the same day of the week. It is also useful for calculating the magnitude and character of eclipses.[12]
- Mackay cycle
- Equals 76 inex plus 9 saros, therefore 2362 years 1 month 4 days or 29215 lunations, always occurring on the same node. Mentioned by A. Mackay in the 1800's.[12]
- Horologia
- Equals 110 inex plus 7 saros, therefore 3310 years 2 months 4 days or 40941 lunations, always occurring on the same node. It is useful for calculating the timing and magnitudes of eclipses as they are approximately an integer number of draconic and anomalistic months and weeks apart, leading to similar eclipses in character and week timing.[12]
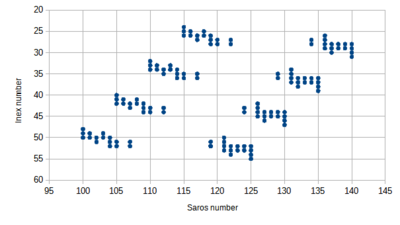
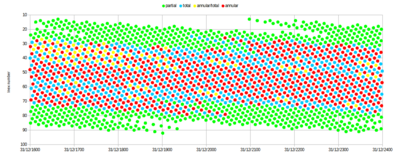
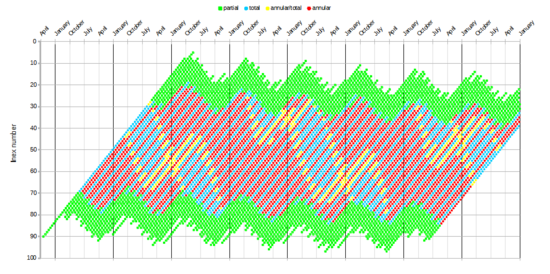
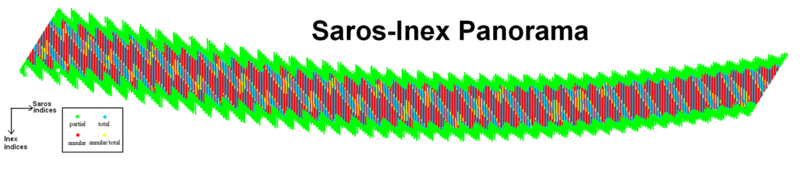
Saros series and inex series
Any eclipse can be assigned to a given saros series and inex series. The year of a solar eclipse (in the Gregorian calendar) is then given approximately by:[21]
- year = 28.945 × number of the saros series + 18.030 × number of the inex series − 2882.55
When this is greater than 1, the integer part gives the year AD, but when it is negative the year BC is obtained by taking the integer part and adding 2. For instance, the eclipse in saros series 0 and inex series 0 was in the middle of 2884 BC. A "panorama" of solar eclipses arranged by saros and inex has been produced by Luca Quaglia and John Tilley showing 61775 solar eclipses from 11001 BC to AD 15000 (see below).[22] Each column of the graph is a complete Saros series which progresses smoothly from partial eclipses into total or annular eclipses and back into partials. Each graph row represents an inex series. Since a saros, of 223 synodic months, is slightly less than a whole number of draconic months, the early eclipses in a saros series (in the upper part of the diagram) occur after the moon goes through its node (the beginning and end of a draconic month), while the later eclipses (in the lower part) occur before the moon goes through its node. Every 18 years, the eclipse occurs on average about half a degree further west with respect to the node, but the progression is not uniform.
|
Saros and inex number can be calculated for an eclipse near a given date.
Saros and inex numbers are also defined for lunar eclipses. A solar eclipse of given saros and inex series will be preceded a fortnight earlier by a lunar eclipse whose saros number is 26 lower and whose inex number is 18 higher, or it will be followed a fortnight later by a lunar eclipse whose saros number is 12 higher and whose inex number is 43 lower. As with solar eclipses, the Gregorian year of a lunar eclipse can be calculated as:
- year = 28.945 × number of the saros series + 18.030 × number of the inex series − 2454.564
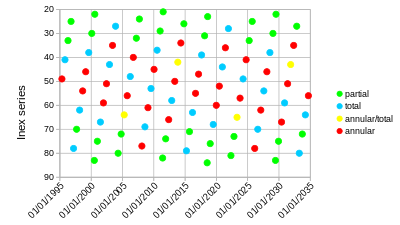
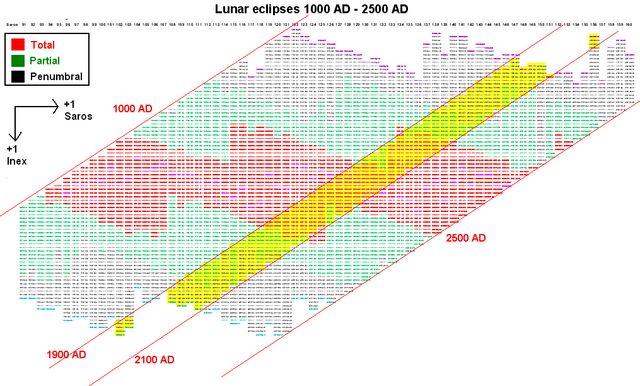
Lunar eclipses can also be plotted in a similar diagram, this diagram covering 1000 AD to 2500 AD. The yellow diagonal band represents all the eclipses from 1900 to 2100. This graph immediately illuminates that this 1900–2100 period contains an above average number of total lunar eclipses compared to other adjacent centuries.
This is related to the fact that tetrads (see above) are more common at present than at other periods. Tetrads occur when four lunar eclipses occur at four lunar inex numbers, decreseing by 8 (that is, a semester apart), which are in the range giving fairly central eclipses (small gamma), and furthermore the eclipses take place around halfway between the earth's perihelion and aphelion. For example, in the tetrad of 2014-2015 (the so-called Four Blood Moons), the inex numbers were 52, 44, 36, and 28, and the eclipses occurred in April and late September-early October. Normally the absolute value of gamma decreases and then increases, but because in April the sun is further east than its mean longitude, and in September/October further west than its mean longitude, the absolute values of gamma in the first and fourth eclipse are decreased, while the absolute values in the second and third are increased. The result is that all four gamma values are small enough to lead to total lunar eclipses. The phenomenon of the moon "catching up" with the sun (or the point opposite the sun), which is usually not at its mean longitude, has been called a "stern chase".[23]
Inex series move slowly through the year, each eclipse occurring about 20 days earlier in the year, 29 years later. This means that over a period of 18.2 inex cycles (526 years) the date moves around the whole year. But because the perihelion of Earth's orbit is slowly moving as well, the inex series that are now producing tetrads will again be halfway between Earth's perihelion and aphelion in about 586 years.[24]
One can skew the graph of inex versus saros for solar or lunar eclipses so that the x axis shows the time of year. (An eclipse which is two saros series and one inex series later than another will be only 1.8 days later in the year.) This shows the 586-year oscillations as oscillations that go up around perihelion and down around aphelion.
See also
References
- ↑ properly, these are periods, not cycles
- ↑ 2.0 2.1 2.2 NASA Periodicity of solar eclipses
- ↑ van Gent, Robert Harry (8 September 2003). "A Catalogue of Eclipse Cycles". http://www.staff.science.uu.nl/~gent0113/eclipse/eclipsecycles.htm.
- ↑ Solar Eclipses: 2011–2020
- ↑ Littmann, Mark; Fred Espenak; Ken Willcox (2008). Totality: Eclipses of the Sun. Oxford University Press. ISBN 978-0-19-953209-4.
- ↑ Periodicity of Lunar and Solar Eclipses, Fred Espenak
- ↑ Five Millennium Catalog of Lunar and Solar Eclipses: -1999 to +3000, Fred Espenak and Jean Meeus
- ↑ Meeus (1991) form. 47.1
- ↑ Meeus (1991) ch. 49 p.334
- ↑ Meeus (1991) form. 48.1
- ↑ 2.170391682 = 2 + 0.170391682 ; 1/0.170391682 = 5 + 0.868831085... ; 1/0.868831085... = 1 +5097171...6237575... ; etc. ; Evaluating this 4th continued fraction: 1/6 + 1 = 7/6; 6/7 + 5 = 41/7 ; 7/41 + 2 = 89/41
- ↑ 12.00 12.01 12.02 12.03 12.04 12.05 12.06 12.07 12.08 12.09 12.10 12.11 12.12 12.13 12.14 12.15 12.16 12.17 12.18 12.19 12.20 12.21 12.22 12.23 12.24 12.25 12.26 12.27 12.28 12.29 12.30 12.31 12.32 12.33 12.34 12.35 12.36 12.37 12.38 12.39 12.40 12.41 12.42 12.43 12.44 12.45 12.46 12.47 12.48 12.49 12.50 12.51 12.52 12.53 12.54 12.55 12.56 12.57 12.58 12.59 12.60 12.61 12.62 Rob van Gent. "A Catalogue of Eclipse Cycles". Utrecht University. https://webspace.science.uu.nl/~gent0113/eclipse/eclipsecycles.htm.
- ↑ A Catalogue of Eclipse Cycles, Robert Harry van Gent
- ↑ A Catalogue of Eclipse Cycles, Robert Harry van Gent
- ↑ A Catalogue of Eclipse Cycles, Robert Harry van Gent
- ↑ 16.0 16.1 See Panorama of Quaglia and Tilley.
- ↑ SE Newsletter February 1999,
- ↑ How often does a solar eclipse happen on the March equinox?,
- ↑ Eminent Lives in Twentieth-century Science & Religion,
- ↑ 29-Year-Eclipse-Cycle,
- ↑ Based on Saros, Inex and Eclipse cycles.
- ↑ Saros-Inex Panorama. Data in Solar eclipse panaorama.xls.
- ↑ John H. Duke (May 20, 2010). "Do periodic consolidations of Pacific countercurrents trigger global cooling by equatorially symmetric La Niña". Climate of the Past Discussions 6 (3): 905. doi:10.5194/cpd-6-905-2010. Bibcode: 2010CliPD...6..905D. https://cp.copernicus.org/preprints/6/905/2010/cpd-6-905-2010-print.pdf. See also Fergus Wood (1976). The Strategic Role of Perigean Spring Tides in Nautical History and North American Coastal Flooding, 1635-1976. https://books.google.com/books?id=k02T9PU19ioC&q=%22stern+chase%22&pg=PA269.
- ↑ John H. Duke (May 20, 2010). "Do periodic consolidations of Pacific countercurrents trigger global cooling by equatorially symmetric La Niña". Climate of the Past Discussions: 928–929. doi:10.5194/cpd-6-905-2010. Bibcode: 2010CliPD...6..905D. https://cp.copernicus.org/preprints/6/905/2010/cpd-6-905-2010-print.pdf. See especially Figures 10 and 13.
- S. Newcomb (1882): On the recurrence of solar eclipses. Astron.Pap.Am.Eph. vol. I pt. I . Bureau of Navigation, Navy Dept., Washington 1882
- J.N. Stockwell (1901): Eclips-cycles. Astron.J. 504 [vol.xx1(24)], 14-Aug-1901
- A.C.D. Crommelin (1901): The 29-year eclipse cycle. Observatory xxiv nr.310, 379, Oct-1901
- A. Pannekoek (1951): Periodicities in Lunar Eclipses. Proc. Kon. Ned. Acad. Wetensch. Ser.B vol.54 pp. 30..41 (1951)
- G. van den Bergh (1954): Eclipses in the second millennium B.C. Tjeenk Willink & Zn NV, Haarlem 1954
- G. van den Bergh (1955): Periodicity and Variation of Solar (and Lunar) Eclipses, 2 vols. Tjeenk Willink & Zn NV, Haarlem 1955
- Jean Meeus (1991): Astronomical Algorithms (1st ed.). Willmann-Bell, Richmond VA 1991; ISBN:0-943396-35-2
- Jean Meeus (1997): Mathematical Astronomy Morsels [I], Ch.9 Solar Eclipses: Some Periodicities (pp. 49..55). Willmann-Bell, Richmond VA 1997; ISBN:0-943396-51-4
- Jean Meeus (2004): Mathematical Astronomy Morsels III, Ch.21 Lunar Tetrads (pp. 123..140). Willmann-Bell, Richmond VA 2004; ISBN:0-943396-81-6
External links
- A Catalogue of Eclipse Cycles (more comprehensive than the above)
- Search 5,000 years worth of eclipses between 2000 BC and AD 3000
- Eclipses, Cosmic Clockwork of the Ancients
- The Saros and the Inex
 |