Astronomy:Gauss's Pythagorean right triangle proposal

From HandWiki
Short description: Idea for signaling extraterrestrial beings from Earth
Visual representation of the Pythagorean theorem. Under the proposal the shape seen here would be drawn at vast size on the Siberian tundra using pine trees and fields of wheat.

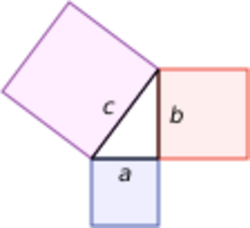
Gauss's Pythagorean right triangle proposal is an idea attributed to Carl Friedrich Gauss for a method to signal extraterrestrial beings by constructing an immense right triangle and three squares on the surface of the Earth. The shapes would be a symbolic representation of the Pythagorean theorem, large enough to be seen from the Moon or Mars.

Although credited in numerous sources as originating with Gauss, with exact details of the proposal set out, the specificity of detail, and even whether Gauss made the proposal, have been called into question. Many of the earliest sources do not actually name Gauss as the originator, instead crediting a "German astronomer" or using other nonspecific descriptors, and in some cases naming a different author entirely. The details of the proposal also change significantly upon different retellings. Nevertheless, Gauss's writings reveal a belief and interest in finding a method to contact extraterrestrial life, and that he did, at the least, propose using amplified light using a heliotrope, his own 1818 invention, to signal supposed inhabitants of the Moon.

Proposal

Carl Friedrich Gauss is credited with an 1820 proposal[1] for a method to signal extraterrestrial beings in the form of drawing an immense right triangle and three squares on the surface of the Earth, intended as a symbolical representation of the Pythagorean theorem, large enough to be seen from the Moon or Mars. Details vary between sources, but typically the "drawing" was to be constructed on the Siberian tundra, and made up of vast strips of pine forest forming the right triangle's borders, with the interior of the drawing and exterior squares composed of fields of wheat.[2] Gauss is said to have been convinced that Mars harbored intelligent life and that this geometric figure, invoking the Pythagorean theorem through the squares on the outside borders[3] (sometimes called a "windmill diagram", as originated by Euclid),[4] would demonstrate to such alien observers the reciprocal existence of intelligent life on Earth and its grounding in mathematics.[5] Wheat was said to be chosen by Gauss for contrast with the pine tree borders "because of its uniform color".[6]

Attribution

The specificity of the proposal's details as it appears in most later sources—even its attribution to Gauss—is called into question in University of Notre Dame Professor Michael J. Crowe's 1986 book, The Extraterrestrial Life Debate, 1750–1900, in which he surveys the origins of the Gauss proposal and observes that:

The history of this proposal ... can be traced through two dozen or more pluralist writings reaching back to the first half of the nineteenth century. When this is done, however, it turns out that the story exists in almost as many forms as its retellings. Furthermore, these versions share one characteristic: Never is reference supplied to where in the writings of Gauss ... the [proposal] appear[s]![4]

Some early sources explored by Crowe for the attribution and form of Gauss's proposal include Austrian astronomer, Joseph Johann Littrow's statement in Wunder des Himmels that "one of our most distinguished geometers"[4] proposed that a geometric figure "for example the well known so-called square of the hypotenuse, be laid out on a large scale, say on a particular broad plain of the earth".[4] and Patrick Scott's Love in the Moon, in which a "learned man" is described as proposing a signal formed by a "great plantation of tree" in the form of "47th Proposition of Euclid" in "the great African desert".[4] In Chambers's Edinburgh Journal it was written that a Russian savant had proposed to "communicate with the moon by cutting a large figure of the forty-seventh proposition of Euclid on the plains of Siberia, which, he said, any fool would understand".[4]

In the writings of astronomers Asaph Hall and of Norman Lockyer, each refer separately to a "German astronomer" who proposed the method of contact be by "fire signals" from Siberia. Writing in 1902, Simon Newcomb placed the origin of a Siberian triangle "several hundred miles in extent" not with Gauss, but at the feet of German astronomer Franz Xaver von Zach. In lectures presented by François Arago at the Paris Observatory, he named Siberia as the location of an extraterrestrial signaling project advanced by an unnamed "German geometer",[4] but that the signaling method was to be through the use of mirrors, rather than any large symbol drawn upon the Earth.[4] Despite this version's departure from a geometric figure, the appearance of mirrors as a signaling device has a connection with Gauss's background. Gauss invented the heliotrope in 1818,[4] an instrument that uses a mirror to reflect sunlight in a manner allowing a 1-inch (2.5 cm) square mirror to be seen 8 miles (13 km) away even in sunny weather.[7]

Gauss wrote of the heliotrope's potential as a celestial signaling device in a March 25, 1822, letter to Heinrich Olbers, by which he reveals a belief and interest in finding a method to contact extraterrestrial life: "With 100 separate mirrors, each of 16 square feet, used conjointly, one would be able to send good heliotrope-light to the moon ... This would be a discovery even greater than that of America, if we could get in touch with our neighbors on the moon."[4] Finally, in the October 1826 issue of the Edinburgh New Philosophical Journal an unnamed author wrote that in a conversation with Franz von Paula Gruithuisen, Gauss stated words to the effect that "the plan of erecting a geometrical figure on the plains of Siberia corresponded with his opinion, because, according to his view a correspondence with the inhabitants of the moon could only be begun by means of such mathematical contemplations and ideas, which we and they have in common."[4] Crowe concluded in sum that his review of earliest sources failed to confirm the detail of the proposal and Gauss as its author, but that his origination of the idea was not unlikely given the existing evidence.[4]

References

  1. ↑ Garelik, Glenn; Nash, J. Madeleine; Woodbury, Richard (July 18, 1988). "Space: Onward to Mars". Time (magazine) 132 (3): 50. http://www.time.com/time/magazine/article/0,9171,967915,00.html. 
  2. ↑ David Kahn (1996). The Codebreakers: The Story of Secret Writing. Simon and Schuster. p. 958. ISBN 978-0-684-83130-5. https://books.google.com/books?id=SEH_rHkgaogC&pg=PA958. 
  3. ↑ Sullivan, Walter (September 29, 1968). "The Universe Is Not Ours Alone; From the edge of the galaxy". The New York Times. https://www.nytimes.com/1968/09/29/archives/the-universe-is-not-oues-alone-from-the-edge-of-the-galaxy.html. 
  4. ↑ 4.00 4.01 4.02 4.03 4.04 4.05 4.06 4.07 4.08 4.09 4.10 4.11 Michael J. Crowe (1999). The Extraterrestrial Life Debate, 1750-1900. Dover Publications. pp. 205–207. ISBN 978-0-486-40675-6. https://books.google.com/books?id=J4TZPlihVUoC&pg=PA205. 
  5. ↑ David E. Fisher; Marshall Fisher (October 8, 1998). Strangers in the Night: A Brief History of Life On Other Worlds. Counterpoint. p. 22. ISBN 978-1-887178-87-7. https://books.google.com/books?id=ntkfAQAAIAAJ. 
  6. ↑ Goldbarth, Albert (Fall 1993). "Worlds". New England Review 15 (4): 17. 
  7. ↑ The New American Encyclopaedia: A Popular Dictionary of General Knowledge. IX. D. Appleton. 1872. p. 63. https://books.google.com/books?id=z-lDAAAAYAAJ&pg=PA63. 



Retrieved from "https://handwiki.org/wiki/index.php?title=Astronomy:Gauss%27s_Pythagorean_right_triangle_proposal&oldid=3355057"