Biggest little polygon
In geometry, the biggest little polygon for a number n is the n-sided polygon that has diameter one (that is, every two of its points are within unit distance of each other) and that has the largest area among all diameter-one n-gons. One non-unique solution when n = 4 is a square, and the solution is a regular polygon when n is an odd number, but the solution is irregular otherwise.
Quadrilaterals
For n = 4, the area of an arbitrary quadrilateral is given by the formula S = pq sin(θ)/2 where p and q are the two diagonals of the quadrilateral and θ is either of the angles they form with each other. In order for the diameter to be at most 1, both p and q must themselves be at most 1. Therefore, the quadrilateral has largest area when the three factors in the area formula are individually maximized, with p = q = 1 and sin(θ) = 1. The condition that p = q means that the quadrilateral is an equidiagonal quadrilateral (its diagonals have equal length), and the condition that sin(θ) = 1 means that it is an orthodiagonal quadrilateral (its diagonals cross at right angles). The quadrilaterals of this type include the square with unit-length diagonals, which has area 1/2. However, infinitely many other orthodiagonal and equidiagonal quadrilaterals also have diameter 1 and have the same area as the square, so in this case the solution is not unique.[1]
Odd numbers of sides
For odd values of n, it was shown by Karl Reinhardt in 1922 that a regular polygon has largest area among all diameter-one polygons.[2]
Even numbers of sides
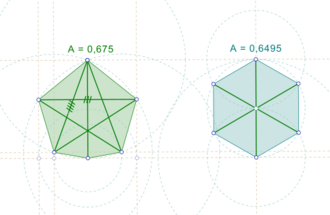
In the case n = 6, the unique optimal polygon is not regular. The solution to this case was published in 1975 by Ronald Graham, answering a question posed in 1956 by Hanfried Lenz;[3] it takes the form of an irregular equidiagonal pentagon with an obtuse isosceles triangle attached to one of its sides, with the distance from the apex of the triangle to the opposite pentagon vertex equal to the diagonals of the pentagon.[4] Its area is 0.674981.... (sequence A111969 in the OEIS), a number that satisfies the equation
- 4096 x10 +8192x9 − 3008x8 − 30848x7 + 21056x6 + 146496x5 − 221360x4 + 1232x3 + 144464x2 − 78488x + 11993 = 0.
Graham conjectured that the optimal solution for the general case of even values of n consists in the same way of an equidiagonal (n − 1)-gon with an isosceles triangle attached to one of its sides, its apex at unit distance from the opposite (n − 1)-gon vertex. In the case n = 8 this was verified by a computer calculation by Audet et al.[5] Graham's proof that his hexagon is optimal, and the computer proof of the n = 8 case, both involved a case analysis of all possible n-vertex thrackles with straight edges.
The full conjecture of Graham, characterizing the solution to the biggest little polygon problem for all even values of n, was proven in 2007 by Foster and Szabo.[6]
See also
- Hansen's small octagon
- Reinhardt polygon, the polygons maximizing perimeter for their diameter, maximizing width for their diameter, and maximizing width for their perimeter
References
- ↑ Schäffer, J. J. (1958), "Nachtrag zu Ungelöste Prob. 12", Elemente der Math. 13: 85–86. As cited by (Graham 1975).
- ↑ Reinhardt, K. (1922), "Extremale Polygone gegebenen Durchmessers", Jahresbericht der Deutschen Mathematiker-Vereinigung 31: 251–270, http://resolver.sub.uni-goettingen.de/purl?PPN37721857X_0031/dmdlog36.
- ↑ Lenz, H. (1956), "Ungelöste Prob. 12", EIemente der Math. 11: 86. As cited by (Graham 1975).
- ↑ Graham, R. L. (1975), "The largest small hexagon", Journal of Combinatorial Theory, Series A 18 (2): 165–170, doi:10.1016/0097-3165(75)90004-7, http://www.math.ucsd.edu/~ronspubs/75_02_hexagon.pdf.
- ↑ Audet, Charles; Hansen, Pierre; Messine, Frédéric; Xiong, Junjie (2002), "The largest small octagon", Journal of Combinatorial Theory, Series A 98 (1): 46–59, doi:10.1006/jcta.2001.3225.
- ↑ Foster, Jim; Szabo, Tamas (2007), "Diameter graphs of polygons and the proof of a conjecture of Graham", Journal of Combinatorial Theory, Series A 114 (8): 1515–1525, doi:10.1016/j.jcta.2007.02.006.
External links
- Weisstein, Eric W.. "Biggest Little Polygon". http://mathworld.wolfram.com/BiggestLittlePolygon.html.
- Graham's Largest Small Hexagon, from the Hall of Hexagons
 |