Biology:De novo protein structure prediction

In computational biology, de novo protein structure prediction refers to an algorithmic process by which protein tertiary structure is predicted from its amino acid primary sequence. The problem itself has occupied leading scientists for decades while still remaining unsolved. According to Science, the problem remains one of the top 125 outstanding issues in modern science. At present, some of the most successful methods have a reasonable probability of predicting the folds of small, single-domain proteins within 1.5 angstroms over the entire structure. De novo methods tend to require vast computational resources, and have thus only been carried out for relatively small proteins. De novo protein structure modeling is distinguished from Template-based modeling (TBM) by the fact that no solved homologue to the protein of interest is used, making efforts to predict protein structure from amino acid sequence exceedingly difficult. Prediction of protein structure de novo for larger proteins will require better algorithms and larger computational resources such as those afforded by either powerful supercomputers (such as Blue Gene or MDGRAPE-3) or distributed computing projects (such as Folding@home, Rosetta@home, the Human Proteome Folding Project, or Nutritious Rice for the World). Although computational barriers are vast, the potential benefits of structural genomics (by predicted or experimental methods) to fields such as medicine and drug design make de novo structure prediction an active research field.

Background

Currently, the gap between known protein sequences and confirmed protein structures is immense. At the beginning of 2008, only about 1% of the sequences listed in the UniProtKB database corresponded to structures in the Protein Data Bank (PDB), leaving a gap between sequence and structure of approximately five million. Experimental techniques for determining tertiary structure have faced serious bottlenecks in their ability to determine structures for particular proteins. For example, whereas X-ray crystallography has been successful in crystallizing approximately 80,000 cytosolic proteins, it has been far less successful in crystallizing membrane proteins – approximately 280. In light of experimental limitations, devising efficient computer programs to close the gap between known sequence and structure is believed to be the only feasible option.

De novo protein structure prediction methods attempt to predict tertiary structures from sequences based on general principles that govern protein folding energetics and/or statistical tendencies of conformational features that native structures acquire, without the use of explicit templates. Research into de novo structure prediction has been primarily focused into three areas: alternate lower-resolution representations of proteins, accurate energy functions, and efficient sampling methods.

A general paradigm for de novo prediction involves sampling conformation space, guided by scoring functions and other sequence-dependent biases such that a large set of candidate (“decoy") structures are generated. Native-like conformations are then selected from these decoys using scoring functions as well as conformer clustering. High-resolution refinement is sometimes used as a final step to fine-tune native-like structures. There are two major classes of scoring functions. Physics-based functions are based on mathematical models describing aspects of the known physics of molecular interaction. Knowledge-based functions are formed with statistical models capturing aspects of the properties of native protein conformations.

Amino Acid Sequence Determines Protein Tertiary Structure

Several lines of evidence have been presented in favor of the notion that primary protein sequence contains all the information required for overall three-dimensional protein structure, making the idea of a de novo protein prediction possible. First, proteins with different functions usually have different amino acid sequences. Second, several different human diseases, such as Duchenne muscular dystrophy, can be linked to loss of protein function resulting from a change in just a single amino acid in the primary sequence. Third, proteins with similar functions across many different species often have similar amino acid sequences. Ubiquitin, for example, is a protein involved in regulating the degradation of other proteins; its amino acid sequence is nearly identical in species as far separated as Drosophila melanogaster and Homo sapiens. Fourth, by thought experiment, one can deduce that protein folding must not be a completely random process and that information necessary for folding must be encoded within the primary structure. For example, if we assume that each of 100 amino acid residues within a small polypeptide could take up 10 different conformations on average, giving 10^100 different conformations for the polypeptide. If one possible conformation was tested every 10^-13 second, then it would take about 10^77 years to sample all possible conformations. However, proteins are properly folded within the body on short timescales all the time, meaning that the process cannot be random and, thus, can potentially be modeled.

One of the strongest lines of evidence for the supposition that all the relevant information needed to encode protein tertiary structure is found in the primary sequence was demonstrated in the 1950s by Christian Anfinsen. In a classic experiment, he showed that ribonuclease A could be entirely denatured by being submerged in a solution of urea (to disrupt stabilizing hydrophobic bonds) in the presence of a reducing agent (to cleave stabilizing disulfide bonds). Upon removal of the protein from this environment, the denatured and functionless ribonuclease protein spontaneously recoiled and regained function, demonstrating that protein tertiary structure is encoded in the primary amino acid sequence. Had the protein reformed randomly, over one-hundred different combinations of four disulfide bonds could have formed. However, in the majority of cases proteins will require the presence of molecular chaperons within the cell for proper folding. The overall shape of a protein may be encoded in its amino acid structure, but its folding may depend on chaperons to assist in folding.

• Primary to Tertiary
• 

  Primary structure of human artemin (Isoform 1 [UniParc])

• 
• 

  Tertiary structure of human artemin (PDB: 2GYR) rendered using PyMOL (Delano Scientific Freeware)

Successful De Novo Modeling Requirements

De novo conformation predictors usually function by producing candidate conformations (decoys) and then choosing amongst them based on their thermodynamic stability and energy state. Most successful predictors will have the following three factors in common:

1) An accurate energy function that corresponds the most thermodynamically stable state to the native structure of a protein

2) An efficient search method capable of quickly identifying low-energy states through conformational search

3) The ability to select native-like models from a collection of decoy structures

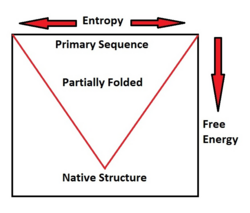
De novo programs will search three dimensional space and, in the process, produce candidate protein conformations. As a protein approaches its correctly folded, native state, entropy and free energy will decrease. Using this information, de novo predictors can discriminate amongst decoys. Specifically, de novo programs will select possible conformations with lower free energies – which are more likely to be correct than those structures with higher free energies. As stated by David A. Baker in regards to how his de novo Rosetta predictor works, “during folding, each local segment of the chain flickers between a different subset of local conformations…folding to the native structure occurs when the conformations adopted by the local segments and their relative orientations allow…low energy features of native protein structures. In the Rosetta algorithm…the program then searches for the combination of these local conformations that has the lowest overall energy.”

However, some de novo methods work by first enumerating through the entire conformational space using a simplified representation of a protein structure, and then select the ones that are most likely to be native-like. An example of this approach is one based on representing protein folds using tetrahedral lattices and building all atoms models on top of all possible conformations obtained using the tetrahedral representation. This approach was used successfully at CASP3 to predict a protein fold whose topology had not been observed before by Michael Levitt's team.

By developing the QUARK program, Xu and Zhang showed that ab initio structure of some proteins can be successfully constructed through a knowledge-based force field .

Correctly folded protein conformations (native structures) have lower free energies than partially folded or primary structures. Computers search for these conformations because they indicate correct folding.

Protein Predicting Strategies

If a protein of known tertiary structure shares at least 30% of its sequence with a potential homolog of undetermined structure, comparative methods that overlay the putative unknown structure with the known can be utilized to predict the likely structure of the unknown. However, below this threshold three other classes of strategy are used to determine possible structure from an initial model: ab initio protein prediction, fold recognition, and threading.

1. Ab Initio Methods: In ab initio methods, an initial effort to elucidate secondary structures (alpha helix, beta sheet, beta turn, etc.) from primary structure is made by utilization of physicochemical parameters and neural net algorithms. From that point, algorithms predict tertiary folding. One drawback to this strategy is that it is not yet capable of incorporating the locations and orientation of amino acid side chains.
2. Fold Prediction: In fold recognition strategies, a prediction of secondary structure is first made and then compared to either a library of known protein folds, such as CATH or SCOP, or what is known as a "periodic table" of possible secondary structure forms. A confidence score is then assigned to likely matches.
3. Threading: In threading strategies, the fold recognition technique is expanded further. In this process, empirically based energy functions for the interaction of residue pairs are used to place the unknown protein onto a putative backbone as a best fit, accommodating gaps where appropriate. The best interactions are then accentuated in order to discriminate amongst potential decoys and to predict the most likely conformation.

The goal of both fold and threading strategies is to ascertain whether a fold in an unknown protein is similar to a domain in a known one deposited in a database, such as the protein databank (PDB). This is in contrast to de novo (ab initio) methods where structure is determined using a physics-base approach en lieu of comparing folds in the protein to structures in a data base.

Limitations of De novo Prediction Methods

A major limitation of de novo protein prediction methods is the extraordinary amount of computer time required to successfully solve for the native conformation of a protein. Distributed methods, such as Rosetta@home, have attempted to ameliorate this by recruiting individuals who then volunteer idle home computer time in order to process data. Even these methods face challenges, however. For example, a distributed method was utilized by a team of researchers at the University of Washington and the Howard Hughes Medical Institute to predict the tertiary structure of the protein T0283 from its amino acid sequence. In a blind test comparing the accuracy of this distributed technique with the experimentally confirmed structure deposited within the Protein Databank (PDB), the predictor produced excellent agreement with the deposited structure. However, the time and number of computers required for this feat was enormous – almost two years and approximately 70,000 home computers, respectively.

One method proposed to overcome such limitations involves the use of Markov models (see Markov chain Monte Carlo). One possibility is that such models could be constructed in order to assist with free energy computation and protein structure prediction, perhaps by refining computational simulations. Another way of circumventing the computational power limitations is using coarse-grained modeling. Coarse-grained protein models allow for de novo structure prediction of small proteins, or large protein fragments, in a short computational time.

An example of distributed computing (Rosetta) in predicting the 3D structure of a protein from its amino-acid sequence. The predicted structure (magenta) of a protein is overlaid with the experimentally determined crystal structure (blue) of that protein. The agreement between the two is very good.

CASP

“Progress for all variants of computational protein structure prediction methods is assessed in the biannual, community wide Critical Assessment of Protein Structure Prediction (CASP) experiments. In the CASP experiments, research groups are invited to apply their prediction methods to amino acid sequences for which the native structure is not known but to be determined and to be published soon. Even though the number of amino acid sequences provided by the CASP experiments is small, these competitions provide a good measure to benchmark methods and progress in the field in an arguably unbiased manner.”

Notes

• Samudrala, R, Xia, Y, Huang, E.S., Levitt, M. Ab initio prediction of protein structure using a combined hierarchical approach. (1999). Proteins Suppl 3: 194-198.
• Bradley, P.; Malmstrom, L.; Qian, B.; Schonbrun, J.; Chivian, D.; Kim, D. E.; Meiler, J.; Misura, K. M. et al. (2005). "Free modeling with Rosetta in CASP6". Proteins 61 (Suppl 7): 128–34. doi:10.1002/prot.20729. PMID 16187354. 
• Bonneau; Baker, D (2001). "Ab Initio Protein Structure Prediction: Progress and Prospects". Annu. Rev. Biophys. Biomol. Struct. 30: 173–89. doi:10.1146/annurev.biophys.30.1.173. PMID 11340057. 
• J. Skolnick, Y. Zhang and A. Kolinski. Ab Initio modeling. Structural genomics and high throughput structural biology. M. Sundsrom, M. Norin and A. Edwards, eds. 2006: 137-162.
• J Lee, S Wu, Y Zhang. Ab initio protein structure prediction. From Protein Structure to Function with Bioinformatics, Chapter 1, Edited by D. J. Rigden, (Springer-London, 2009), P. 1-26.

See also

• Protein structure prediction
• Protein structure prediction software
• Protein design

External links

• CASP
• Folding@Home
• HPF project
• Foldit
• UniProtKB
• Protein Data Bank (PDB)
• Expert Protein Analysis System - links to protein prediction tools