Physics:X-ray crystallography

Short description: Technique used for determining crystal structures and identifying mineral compounds

A powder X-ray diffractometer in motion

X-ray crystallography is the experimental science determining the atomic and molecular structure of a crystal, in which the crystalline structure causes a beam of incident X-rays to diffract into many specific directions. By measuring the angles and intensities of these diffracted beams, a crystallographer can produce a three-dimensional picture of the density of electrons within the crystal. From this electron density, the positions of the atoms in the crystal can be determined, as well as their chemical bonds, crystallographic disorder, and various other information.

Since many materials form crystals—such as salts, metals, minerals, semiconductors, as well as various inorganic, organic, and biological molecules—X-ray crystallography has been fundamental in the development of many scientific fields. In its first decades of use, this method determined the size of atoms, the lengths and types of chemical bonds, and the atomic-scale differences between various materials, especially minerals and alloys. The method also revealed the structure and function of many biological molecules, including vitamins, drugs, proteins and nucleic acids such as DNA. X-ray crystallography is still the primary method for characterizing the atomic structure of new materials and in discerning materials that appear similar in other experiments. X-ray crystal structures can also account for unusual electronic or elastic properties of a material, shed light on chemical interactions and processes, or serve as the basis for designing pharmaceuticals against diseases.

X-ray crystallography is related to multiple other methods for determining atomic structures. Similar diffraction patterns can be produced by scattering electrons or neutrons. If single crystals of sufficient size cannot be obtained, various other X-ray methods can be applied to obtain less detailed information; such methods include fiber diffraction, powder diffraction and (if the sample is not crystallized) small-angle X-ray scattering (SAXS). If the material under investigation is only available in the form of nanocrystalline powders or suffers from poor crystallinity, the methods of electron diffraction, transmission electron microscopy, and electron crystallography can be applied for determining the atomic structure.

History

Drawing of square (A) and hexagonal (B) packing from Kepler's work, Strena seu de Nive Sexangula.

The hexagonal symmetry of snowflakes results from the tetrahedral arrangement of hydrogen bonds about each water molecule.

Crystals, though long admired for their regularity and symmetry, were not investigated scientifically until the 17th century. Johannes Kepler hypothesized in his work Strena seu de Nive Sexangula (A New Year's Gift of Hexagonal Snow) (1611) that the hexagonal symmetry of snowflake crystals was due to a regular packing of spherical water particles. The Danish scientist Nicolas Steno (1669) pioneered experimental investigations of crystal symmetry. Steno showed that the angles between the faces are the same in every exemplar of a particular type of crystal. René Just Haüy (1784) discovered that every face of a crystal can be described by simple stacking patterns of blocks of the same shape and size. Hence, William Hallowes Miller in 1839 was able to give each face a unique label of three small integers, the Miller indices which remain in use for identifying crystal faces. Haüy's study led to the idea that crystals are a regular three-dimensional array (a Bravais lattice) of atoms and molecules; a single unit cell is repeated indefinitely along three principal directions. In the 19th century, a complete catalog of the possible symmetries of a crystal was worked out by Johan Hessel, Auguste Bravais, Evgraf Fedorov, Arthur Schönflies and (belatedly) William Barlow (1894). Barlow proposed several crystal structures in the 1880s that were validated later by X-ray crystallography; however, the available data were too scarce in the 1880s to accept his models as conclusive.

Model of the arrangement of water molecules in ice, revealing the hydrogen bonds (1) that hold the solid together.

Wilhelm Röntgen discovered X-rays in 1895. Physicists were uncertain of the nature of X-rays, but suspected that they were waves of electromagnetic radiation. The Maxwell theory of electromagnetic radiation was well accepted, and experiments by Charles Glover Barkla showed that X-rays exhibited phenomena associated with electromagnetic waves, including transverse polarization and spectral lines akin to those observed in the visible wavelengths. Barkla created the x-ray notation for sharp spectral lines, noting in 1909 two separate energies, at first, naming them "A" and "B" and then supposing that there may be lines prior to "A", he started an alphabet numbering beginning with "K." Single-slit experiments in the laboratory of Arnold Sommerfeld suggested that X-rays had a wavelength of about 1 angstrom. X-rays are not only waves but also have particle properties causing Sommerfeld to coin the name Bremsstrahlung for the continuous spectra when they were formed when electrons bombarded a material. Albert Einstein introduced the photon concept in 1905, but it was not broadly accepted until 1922, when Arthur Compton confirmed it by the scattering of X-rays from electrons. The particle-like properties of X-rays, such as their ionization of gases, had prompted William Henry Bragg to argue in 1907 that X-rays were not electromagnetic radiation. Bragg's view proved unpopular and the observation of X-ray diffraction by Max von Laue in 1912 confirmed that X-rays are a form of electromagnetic radiation.

One of the copper sulfate X-ray interference patterns published in Von Laue's 1912 paper.

The idea that crystals could be used as a diffraction grating for X-rays arose in 1912 in a conversation between Paul Peter Ewald and Max von Laue in the English Garden in Munich. Ewald had proposed a resonator model of crystals for his thesis, but this model could not be validated using visible light, since the wavelength was much larger than the spacing between the resonators. Von Laue realized that electromagnetic radiation of a shorter wavelength was needed, and suggested that X-rays might have a wavelength comparable to the unit-cell spacing in crystals. Von Laue worked with two technicians, Walter Friedrich and his assistant Paul Knipping, to shine a beam of X-rays through a copper sulfate crystal and record its diffraction on a photographic plate. After being developed, the plate showed a large number of well-defined spots arranged in a pattern of intersecting circles around the spot produced by the central beam. The results were presented to the Bavarian Academy of Sciences and Humanities on June 1912 as "Interferenz-Erscheinungen bei Röntgenstrahlen" (Interference phenomena in X-rays). Von Laue developed a law that connects the scattering angles and the size and orientation of the unit-cell spacings in the crystal, for which he was awarded the Nobel Prize in Physics in 1914.

Although diamonds (top left) and graphite (top right) are identical in chemical composition—being both pure carbon—X-ray crystallography revealed the arrangement of their atoms (bottom). In diamond, the carbon atoms are arranged tetrahedrally and held together by single covalent bonds. By contrast, graphite is composed of stacked sheets. Within the sheet, the bonding is covalent and has hexagonal symmetry, but there are no covalent bonds between the sheets.

After Von Laue's pioneering research, the field developed rapidly, most notably by physicists William Lawrence Bragg and his father William Henry Bragg. In 1912–1913, the younger Bragg developed Bragg's law, which connects the scattering with evenly spaced planes within a crystal. The Braggs, father and son, shared the 1915 Nobel Prize in Physics for their work in crystallography. The earliest structures were generally simple; as computational and experimental methods improved over the next decades, it became feasible to deduce reliable atomic positions for more complicated arrangements of atoms.

The earliest structures were simple inorganic crystals and minerals, but even these revealed fundamental laws of physics and chemistry. The first atomic-resolution structure to be "solved" (i.e., determined) in 1914 was that of table salt. The distribution of electrons in the table-salt structure showed that crystals are not necessarily composed of covalently bonded molecules, and proved the existence of ionic compounds. The structure of diamond was solved in the same year, proving the tetrahedral arrangement of its chemical bonds and showing that the length of C–C single bond was about 1.52 angstroms. Other early structures included copper, calcium fluoride (CaF₂, also known as fluorite), calcite (CaCO₃) and pyrite (FeS₂) in 1914; spinel (MgAl₂O₄) in 1915; the rutile and anatase forms of titanium dioxide (TiO₂) in 1916; pyrochroite (Mn(OH)₂) and, by extension, brucite (Mg(OH)₂) in 1919. Also in 1919, sodium nitrate (NaNO₃) and caesium dichloroiodide (CsICl₂) were determined by Ralph Walter Graystone Wyckoff, and the wurtzite (hexagonal ZnS) structure was determined in 1920.

The structure of graphite was solved in 1916 by the related method of powder diffraction, which was developed by Peter Debye and Paul Scherrer and, independently, by Albert Hull in 1917. The structure of graphite was determined from single-crystal diffraction in 1924 by two groups independently. Hull also used the powder method to determine the structures of various metals, such as iron and magnesium.

Contributions in different areas

Chemistry

X-ray crystallography has led to a better understanding of chemical bonds and non-covalent interactions. The initial studies revealed the typical radii of atoms, and confirmed many theoretical models of chemical bonding, such as the tetrahedral bonding of carbon in the diamond structure, the octahedral bonding of metals observed in ammonium hexachloroplatinate (IV), and the resonance observed in the planar carbonate group and in aromatic molecules. Kathleen Lonsdale's 1928 structure of hexamethylbenzene established the hexagonal symmetry of benzene and showed a clear difference in bond length between the aliphatic C–C bonds and aromatic C–C bonds; this finding led to the idea of resonance between chemical bonds, which had profound consequences for the development of chemistry. Her conclusions were anticipated by William Henry Bragg, who published models of naphthalene and anthracene in 1921 based on other molecules, an early form of molecular replacement.

The first structure of an organic compound, hexamethylenetetramine, was solved in 1923. This was rapidly followed by several studies of different long-chain fatty acids, which are an important component of biological membranes. In the 1930s, the structures of much larger molecules with two-dimensional complexity began to be solved. A significant advance was the structure of phthalocyanine, a large planar molecule that is closely related to porphyrin molecules important in biology, such as heme, corrin and chlorophyll.

In the 1920s, Victor Moritz Goldschmidt and later Linus Pauling developed rules for eliminating chemically unlikely structures and for determining the relative sizes of atoms. These rules led to the structure of brookite (1928) and an understanding of the relative stability of the rutile, brookite and anatase forms of titanium dioxide.

The distance between two bonded atoms is a sensitive measure of the bond strength and its bond order; thus, X-ray crystallographic studies have led to the discovery of even more exotic types of bonding in inorganic chemistry, such as metal-metal double bonds, metal-metal quadruple bonds, and three-center, two-electron bonds. X-ray crystallography—or, strictly speaking, an inelastic Compton scattering experiment—has also provided evidence for the partly covalent character of hydrogen bonds. In the field of organometallic chemistry, the X-ray structure of ferrocene initiated scientific studies of sandwich compounds, while that of Zeise's salt stimulated research into "back bonding" and metal-pi complexes. Finally, X-ray crystallography had a pioneering role in the development of supramolecular chemistry, particularly in clarifying the structures of the crown ethers and the principles of host–guest chemistry.

Materials science and mineralogy

First X-ray diffraction view of Martian soil – CheMin analysis reveals feldspar, pyroxenes, olivine and more (Curiosity rover at "Rocknest", October 17, 2012).

The application of X-ray crystallography to mineralogy began with the structure of garnet, which was determined in 1924 by Menzer. A systematic X-ray crystallographic study of the silicates was undertaken in the 1920s. This study showed that, as the Si/O ratio is altered, the silicate crystals exhibit significant changes in their atomic arrangements. Machatschki extended these insights to minerals in which aluminium substitutes for the silicon atoms of the silicates. The first application of X-ray crystallography to metallurgy likewise occurred in the mid-1920s. Most notably, Linus Pauling's structure of the alloy Mg₂Sn led to his theory of the stability and structure of complex ionic crystals. Many complicated inorganic and organometallic systems have been analyzed using single-crystal methods, such as fullerenes, metalloporphyrins, and other complicated compounds. Single-crystal diffraction is also used in the pharmaceutical industry. The Cambridge Structural Database contains over 1,000,000 structures as of June 2019; over 99% of these structures were determined by X-ray diffraction.

On October 17, 2012, the Curiosity rover on the planet Mars at "Rocknest" performed the first X-ray diffraction analysis of Martian soil. The results from the rover's CheMin analyzer revealed the presence of several minerals, including feldspar, pyroxenes and olivine, and suggested that the Martian soil in the sample was similar to the "weathered basaltic soils" of Hawaiian volcanoes.

The three-dimensional structure of penicillin, solved by Dorothy Crowfoot Hodgkin in 1945. The green, red, yellow and blue spheres represent atoms of carbon, oxygen, sulfur and nitrogen, respectively. The white spheres represent hydrogen, which were determined mathematically rather than by the X-ray analysis.

Biological macromolecular crystallography

X-ray crystallography of biological molecules took off with Dorothy Crowfoot Hodgkin, who solved the structures of cholesterol (1937), penicillin (1946) and vitamin B₁₂ (1956), for which she was awarded the Nobel Prize in Chemistry in 1964. In 1969, she succeeded in solving the structure of insulin, on which she worked for over thirty years.

Ribbon diagram of the structure of myoglobin, showing alpha helices. Such proteins are long, linear molecules with thousands of atoms; yet the relative position of each atom has been determined with sub-atomic resolution by X-ray crystallography. Since it is difficult to visualize all the atoms at once, the ribbon shows the rough path of the protein's backbone from its N-terminus to its C-terminus.

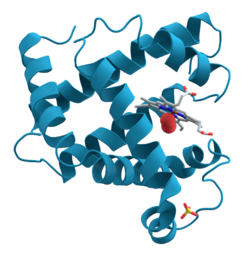
Crystal structures of proteins (which are irregular and hundreds of times larger than cholesterol) began to be solved in the late 1950s, beginning with the structure of sperm whale myoglobin by Sir John Cowdery Kendrew, for which he shared the Nobel Prize in Chemistry with Max Perutz in 1962. Since that success, over 130,000 X-ray crystal structures of proteins, nucleic acids and other biological molecules have been determined. The nearest competing method in number of structures analyzed is nuclear magnetic resonance (NMR) spectroscopy, which has resolved less than one tenth as many. Crystallography can solve structures of arbitrarily large molecules, whereas solution-state NMR is restricted to relatively small ones (less than 70 kDa). X-ray crystallography is used routinely to determine how a pharmaceutical drug interacts with its protein target and what changes might improve it. However, intrinsic membrane proteins remain challenging to crystallize because they require detergents or other denaturants to solubilize them in isolation, and such detergents often interfere with crystallization. Membrane proteins are a large component of the genome, and include many proteins of great physiological importance, such as ion channels and receptors. Helium cryogenics are used to prevent radiation damage in protein crystals.

Methods

Overview of single-crystal X-ray diffraction

Workflow for solving the structure of a molecule by X-ray crystallography.

The oldest and most precise method of X-ray crystallography is single-crystal X-ray diffraction, in which a beam of X-rays strikes a single crystal, producing scattered beams which are recorded as the crystal is gradually rotated. For single crystals of sufficient purity and regularity, X-ray diffraction data can determine the mean chemical bond lengths and angles to within a few thousandths of an angstrom and to within a few tenths of a degree, respectively. The atoms in a crystal are not static, but oscillate about their mean positions, usually by less than a few tenths of an angstrom. X-ray crystallography can measure the size of these oscillations.

Two limiting cases of X-ray crystallography—"small-molecule" (which includes continuous inorganic solids) and "macromolecular" crystallography—are often used. Small-molecule crystallography typically involves crystals with fewer than 100 atoms in their asymmetric unit; such crystal structures are usually so well resolved that the atoms can be discerned as isolated "blobs" of electron density. In contrast, macromolecular crystallography often involves tens of thousands of atoms in the unit cell. Such crystal structures are generally less well-resolved; the atoms and chemical bonds appear as tubes of electron density, rather than as isolated atoms. In general, small molecules are also easier to crystallize than macromolecules; however, X-ray crystallography has proven possible even for viruses and proteins with hundreds of thousands of atoms, through improved crystallographic imaging and technology.

Procedure

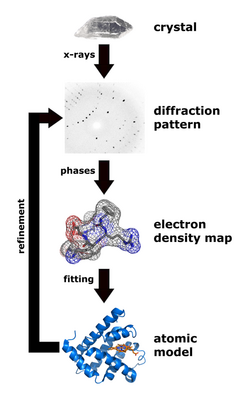
The technique of single-crystal X-ray crystallography has three basic steps. The first—and often most difficult—step is to obtain an adequate crystal of the material under study. The crystal should be sufficiently large (typically larger than 0.1 mm in all dimensions), pure in composition and regular in structure, with no significant internal imperfections such as cracks or twinning.

In the second step, the crystal is placed in an intense beam of X-rays, usually of a single wavelength (monochromatic X-rays), producing the regular pattern of reflections. The angles and intensities of diffracted X-rays are measured, with each compound having a unique diffraction pattern. As the crystal is gradually rotated, previous reflections disappear and new ones appear; the intensity of every spot is recorded at every orientation of the crystal. Multiple data sets may have to be collected, with each set covering slightly more than half a full rotation of the crystal and typically containing tens of thousands of reflections.

In the third step, these data are combined computationally with complementary chemical information to produce and refine a model of the arrangement of atoms within the crystal. The final, refined model of the atomic arrangement—now called a crystal structure—is usually stored in a public database.

Crystallization

A protein crystal seen under a microscope. Crystals used in X-ray crystallography may be smaller than a millimeter across.

Although crystallography can be used to characterize the disorder in an impure or irregular crystal, crystallography generally requires a pure crystal of high regularity to solve the structure of a complicated arrangement of atoms. Pure, regular crystals can sometimes be obtained from natural or synthetic materials, such as samples of metals, minerals or other macroscopic materials. The regularity of such crystals can sometimes be improved with macromolecular crystal annealing and other methods. However, in many cases, obtaining a diffraction-quality crystal is the chief barrier to solving its atomic-resolution structure.

Small-molecule and macromolecular crystallography differ in the range of possible techniques used to produce diffraction-quality crystals. Small molecules generally have few degrees of conformational freedom, and may be crystallized by a wide range of methods, such as chemical vapor deposition and recrystallization. By contrast, macromolecules generally have many degrees of freedom and their crystallization must be carried out so as to maintain a stable structure. For example, proteins and larger RNA molecules cannot be crystallized if their tertiary structure has been unfolded; therefore, the range of crystallization conditions is restricted to solution conditions in which such molecules remain folded.

Three methods of preparing crystals, A: Hanging drop. B: Sitting drop. C: Microdialysis

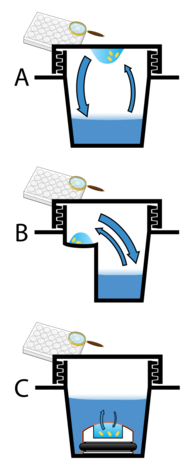
Protein crystals are almost always grown in solution. The most common approach is to lower the solubility of its component molecules very gradually; if this is done too quickly, the molecules will precipitate from solution, forming a useless dust or amorphous gel on the bottom of the container. Crystal growth in solution is characterized by two steps: nucleation of a microscopic crystallite (possibly having only 100 molecules), followed by growth of that crystallite, ideally to a diffraction-quality crystal. The solution conditions that favor the first step (nucleation) are not always the same conditions that favor the second step (subsequent growth). The solution conditions should disfavor the first step (nucleation) but favor the second (growth), so that only one large crystal forms per droplet. If nucleation is favored too much, a shower of small crystallites will form in the droplet, rather than one large crystal; if favored too little, no crystal will form whatsoever. Other approaches involve crystallizing proteins under oil, where aqueous protein solutions are dispensed under liquid oil, and water evaporates through the layer of oil. Different oils have different evaporation permeabilities, therefore yielding changes in concentration rates from different percipient/protein mixture.

It is difficult to predict good conditions for nucleation or growth of well-ordered crystals. In practice, favorable conditions are identified by screening; a very large batch of the molecules is prepared, and a wide variety of crystallization solutions are tested. Hundreds, even thousands, of solution conditions are generally tried before finding the successful one. The various conditions can use one or more physical mechanisms to lower the solubility of the molecule; for example, some may change the pH, some contain salts of the Hofmeister series or chemicals that lower the dielectric constant of the solution, and still others contain large polymers such as polyethylene glycol that drive the molecule out of solution by entropic effects. It is also common to try several temperatures for encouraging crystallization, or to gradually lower the temperature so that the solution becomes supersaturated. These methods require large amounts of the target molecule, as they use high concentration of the molecule(s) to be crystallized. Due to the difficulty in obtaining such large quantities (milligrams) of crystallization-grade protein, robots have been developed that are capable of accurately dispensing crystallization trial drops that are in the order of 100 nanoliters in volume. This means that 10-fold less protein is used per experiment when compared to crystallization trials set up by hand (in the order of 1 microliter).

Several factors are known to inhibit or mar crystallization. The growing crystals are generally held at a constant temperature and protected from shocks or vibrations that might disturb their crystallization. Impurities in the molecules or in the crystallization solutions are often inimical to crystallization. Conformational flexibility in the molecule also tends to make crystallization less likely, due to entropy. Molecules that tend to self-assemble into regular helices are often unwilling to assemble into crystals. Crystals can be marred by twinning, which can occur when a unit cell can pack equally favorably in multiple orientations; although recent advances in computational methods may allow solving the structure of some twinned crystals. Having failed to crystallize a target molecule, a crystallographer may try again with a slightly modified version of the molecule; even small changes in molecular properties can lead to large differences in crystallization behavior.

Data collection

Mounting the crystal

File:Kappa goniometer animation.ogg

The crystal is mounted for measurements so that it may be held in the X-ray beam and rotated. There are several methods of mounting. In the past, crystals were loaded into glass capillaries with the crystallization solution (the mother liquor). Nowadays, crystals of small molecules are typically attached with oil or glue to a glass fiber or a loop, which is made of nylon or plastic and attached to a solid rod. Protein crystals are scooped up by a loop, then flash-frozen with liquid nitrogen. This freezing reduces the radiation damage of the X-rays, as well as the noise in the Bragg peaks due to thermal motion (the Debye-Waller effect). However, untreated protein crystals often crack if flash-frozen; therefore, they are generally pre-soaked in a cryoprotectant solution before freezing. This pre-soak may itself cause the crystal to crack, ruining it for crystallography. Generally, successful cryo-conditions are identified by trial and error.

The capillary or loop is mounted on a goniometer, which allows it to be positioned accurately within the X-ray beam and rotated. Since both the crystal and the beam are often very small, the crystal must be centered within the beam to within ~25 micrometers accuracy, which is aided by a camera focused on the crystal. The most common type of goniometer is the "kappa goniometer", which offers three angles of rotation: the ω angle, which rotates about an axis perpendicular to the beam; the κ angle, about an axis at ~50° to the ω axis; and, finally, the φ angle about the loop/capillary axis. When the κ angle is zero, the ω and φ axes are aligned. The κ rotation allows for convenient mounting of the crystal, since the arm in which the crystal is mounted may be swung out towards the crystallographer. The oscillations carried out during data collection (mentioned below) involve the ω axis only. An older type of goniometer is the four-circle goniometer, and its relatives such as the six-circle goniometer.

Recording the reflections

An X-ray diffraction pattern of a crystallized enzyme. The pattern of spots (reflections) and the relative strength of each spot (intensities) can be used to determine the structure of the enzyme.

The relative intensities of the reflections provides information to determine the arrangement of molecules within the crystal in atomic detail. The intensities of these reflections may be recorded with photographic film, an area detector (such as a pixel detector) or with a charge-coupled device (CCD) image sensor. The peaks at small angles correspond to low-resolution data, whereas those at high angles represent high-resolution data; thus, an upper limit on the eventual resolution of the structure can be determined from the first few images. Some measures of diffraction quality can be determined at this point, such as the mosaicity of the crystal and its overall disorder, as observed in the peak widths. Some pathologies of the crystal that would render it unfit for solving the structure can also be diagnosed quickly at this point.

One set of spots is insufficient to reconstruct the whole crystal; it represents only a small slice of the full three dimensional set. To collect all the necessary information, the crystal must be rotated step-by-step through 180°, with an image recorded at every step; actually, slightly more than 180° is required to cover reciprocal space, due to the curvature of the Ewald sphere. However, if the crystal has a higher symmetry, a smaller angular range such as 90° or 45° may be recorded. The rotation axis should be changed at least once, to avoid developing a "blind spot" in reciprocal space close to the rotation axis. It is customary to rock the crystal slightly (by 0.5–2°) to catch a broader region of reciprocal space.

Multiple data sets may be necessary for certain phasing methods. For example, multi-wavelength anomalous dispersion phasing requires that the scattering be recorded at least three (and usually four, for redundancy) wavelengths of the incoming X-ray radiation. A single crystal may degrade too much during the collection of one data set, owing to radiation damage; in such cases, data sets on multiple crystals must be taken.

Crystal symmetry, unit cell, and image scaling

Further information: Space group

The recorded series of two-dimensional diffraction patterns, each corresponding to a different crystal orientation, is converted into a three-dimensional set. Data processing begins with indexing the reflections. This means identifying the dimensions of the unit cell and which image peak corresponds to which position in reciprocal space. A byproduct of indexing is to determine the symmetry of the crystal, i.e., its space group. Some space groups can be eliminated from the beginning. For example, reflection symmetries cannot be observed in chiral molecules; thus, only 65 space groups of 230 possible are allowed for protein molecules which are almost always chiral. Indexing is generally accomplished using an autoindexing routine. Having assigned symmetry, the data is then integrated. This converts the hundreds of images containing the thousands of reflections into a single file, consisting of (at the very least) records of the Miller index of each reflection, and an intensity for each reflection (at this state the file often also includes error estimates and measures of partiality (what part of a given reflection was recorded on that image)).

A full data set may consist of hundreds of separate images taken at different orientations of the crystal. These have to be merged and scaled usingpeaks appear in two or more images (merging) and scaling so there is a consistent intensity scale. Optimizing the intensity scale is critical because the relative intensity of the peaks is the key information from which the structure is determined. The repetitive technique of crystallographic data collection and the often high symmetry of crystalline materials cause the diffractometer to record many symmetry-equivalent reflections multiple times. This allows calculating the symmetry-related R-factor, a reliability index based upon how similar are the measured intensities of symmetry-equivalent reflections, thus assessing the quality of the data.

Initial phasing

Further information: Phase problem

The intensity of each diffraction 'spot' is proportional to the modulus squared of the structure factor. The structure factor is a complex number containing information relating to both the amplitude and phase of a wave. In order to obtain an interpretable electron density map, both amplitude and phase must be known (an electron density map allows a crystallographer to build a starting model of the molecule). The phase cannot be directly recorded during a diffraction experiment: this is known as the phase problem. Initial phase estimates can be obtained in a variety of ways:

• Ab initio phasing or direct methods – This is usually the method of choice for small molecules (<1000 non-hydrogen atoms), and has been used successfully to solve the phase problems for small proteins. If the resolution of the data is better than 1.4 Å (140 pm), direct methods can be used to obtain phase information, by exploiting known phase relationships between certain groups of reflections.
• Molecular replacement – if a related structure is known, it can be used as a search model in molecular replacement to determine the orientation and position of the molecules within the unit cell. The phases obtained this way can be used to generate electron density maps.
• Anomalous X-ray scattering (MAD or SAD phasing) – the X-ray wavelength may be scanned past an absorption edge of an atom, which changes the scattering in a known way. By recording full sets of reflections at three different wavelengths (far below, far above and in the middle of the absorption edge) one can solve for the substructure of the anomalously diffracting atoms and hence the structure of the whole molecule. The most popular method of incorporating anomalous scattering atoms into proteins is to express the protein in a methionine auxotroph (a host incapable of synthesizing methionine) in a media rich in seleno-methionine, which contains selenium atoms. A multi-wavelength anomalous dispersion (MAD) experiment can then be conducted around the absorption edge, which should then yield the position of any methionine residues within the protein, providing initial phases.
• Heavy atom methods (multiple isomorphous replacement) – If electron-dense metal atoms can be introduced into the crystal, direct methods or Patterson-space methods can be used to determine their location and to obtain initial phases. Such heavy atoms can be introduced either by soaking the crystal in a heavy atom-containing solution, or by co-crystallization (growing the crystals in the presence of a heavy atom). As in multi-wavelength anomalous dispersion phasing, the changes in the scattering amplitudes can be interpreted to yield the phases. Although this is the original method by which protein crystal structures were solved, it has largely been superseded by multi-wavelength anomalous dispersion phasing with selenomethionine.

Model building and phase refinement

Structure of a protein alpha helix, with stick-figures for the covalent bonding within electron density for the crystal structure at ultra-high-resolution (0.91 Å). The density contours are in gray, the helix backbone in white, sidechains in cyan, O atoms in red, N atoms in blue, and hydrogen bonds as green dotted lines.

3D depiction of electron density (blue) of a ligand (orange) bound to a binding site in a protein (yellow). The electron density is obtained from experimental data, and the ligand is modeled into this electron density.

Having obtained initial phases, an initial model can be built. The atomic positions in the model and their respective Debye-Waller factors (or B-factors, accounting for the thermal motion of the atom) can be refined to fit the observed diffraction data, ideally yielding a better set of phases. A new model can then be fit to the new electron density map and successive rounds of refinement are carried out. This iterative process continues until the correlation between the diffraction data and the model is maximized. The agreement is measured by an R-factor defined as

[math]\displaystyle{ R = \frac{\sum_{\text{all reflections}} \left|F_\text{obs} - F_\text{calc} \right|}{\sum_{\text{all reflections}} \left|F_\text{obs} \right|}, }[/math]

where F is the structure factor. A similar quality criterion is R_free, which is calculated from a subset (~10%) of reflections that were not included in the structure refinement. Both R factors depend on the resolution of the data. As a rule of thumb, R_free should be approximately the resolution in angstroms divided by 10; thus, a data-set with 2 Å resolution should yield a final R_free ~ 0.2. Chemical bonding features such as stereochemistry, hydrogen bonding and distribution of bond lengths and angles are complementary measures of the model quality. In iterative model building, it is common to encounter phase bias or model bias: because phase estimations come from the model, each round of calculated map tends to show density wherever the model has density, regardless of whether there truly is a density. This problem can be mitigated by maximum-likelihood weighting and checking using omit maps.

It may not be possible to observe every atom in the asymmetric unit. In many cases, crystallographic disorder smears the electron density map. Weakly scattering atoms such as hydrogen are routinely invisible. It is also possible for a single atom to appear multiple times in an electron density map, e.g., if a protein sidechain has multiple (<4) allowed conformations. In still other cases, the crystallographer may detect that the covalent structure deduced for the molecule was incorrect, or changed. For example, proteins may be cleaved or undergo post-translational modifications that were not detected prior to the crystallization.

Disorder

A common challenge in refinement of crystal structures results from crystallographic disorder. Disorder can take many forms but in general involves the coexistence of two or more species or conformations. Failure to recognize disorder results in flawed interpretation. Pitfalls from improper modeling of disorder are illustrated by the discounted hypothesis of bond stretch isomerism. Disorder is modelled with respect to the relative population of the components, often only two, and their identity. In structures of large molecules and ions, solvent and counterions are often disordered.

Applied computational data analysis

The use of computational methods for the powder X-ray diffraction data analysis is now generalized. It typically compares the experimental data to the simulated diffractogram of a model structure, taking into account the instrumental parameters, and refines the structural or microstructural parameters of the model using least squares based minimization algorithm. Most available tools allowing phase identification and structural refinement are based on the Rietveld method, some of them being open and free software such as FullProf Suite, Jana2006, MAUD, Rietan, GSAS, etc. while others are available under commercial licenses such as Diffrac.Suite TOPAS, Match!, etc. Most of these tools also allow Le Bail refinement (also referred to as profile matching), that is, refinement of the cell parameters based on the Bragg peaks positions and peak profiles, without taking into account the crystallographic structure by itself. More recent tools allow the refinement of both structural and microstructural data, such as the FAULTS program included in the FullProf Suite, which allows the refinement of structures with planar defects (e.g. stacking faults, twinnings, intergrowths).

Deposition of the structure

Once the model of a molecule's structure has been finalized, it is often deposited in a crystallographic database such as the Cambridge Structural Database (for small molecules), the Inorganic Crystal Structure Database (ICSD) (for inorganic compounds) or the Protein Data Bank (for protein and sometimes nucleic acids). Many structures obtained in private commercial ventures to crystallize medicinally relevant proteins are not deposited in public crystallographic databases.

X-ray sources

Further information: Engineering:Diffractometer, Engineering:Synchrotron light source, and Physics:Free-electron laser

Rotating anode

Small scale crystallography can be done with a local X-ray tube source, typically coupled with an image plate detector. These have the advantage of being relatively inexpensive and easy to maintain, and allow for quick screening and collection of samples. However, the wavelength of the light produced is limited by the availability of different anode materials. Furthermore, the intensity is limited by the power applied and cooling capacity available to avoid melting the anode. In such systems, electrons are boiled off of a cathode and accelerated through a strong electric potential of ~50 kV; having reached a high speed, the electrons collide with a metal plate, emitting bremsstrahlung and some strong spectral lines corresponding to the excitation of inner-shell electrons of the metal. The most common metal used is copper, which can be kept cool easily, due to its high thermal conductivity, and which produces strong K_α and K_β lines. The K_β line is sometimes suppressed with a thin (~10 µm) nickel foil. The simplest and cheapest variety of sealed X-ray tube has a stationary anode (the Crookes tube) and run with ~2 kW of electron beam power. The more expensive variety has a rotating-anode type source that runs with ~14 kW of e-beam power.

X-rays are generally filtered (by use of X-ray filters) to a single wavelength (made monochromatic) and collimated to a single direction before they are allowed to strike the crystal. The filtering not only simplifies the data analysis, but also removes radiation that degrades the crystal without contributing useful information. Collimation is done either with a collimator (basically, a long tube) or with a clever arrangement of gently curved mirrors. Mirror systems are preferred for small crystals (under 0.3 mm) or with large unit cells (over 150 Å).

Microfocus tube

A more recent development is the microfocus tube, which can deliver at least as high a beam flux (after collimation) as rotating-anode sources but only require a beam power of a few tens or hundreds of watts rather than requiring several kilowatts.

Synchrotron radiation

Synchrotron radiation sources are some of the brightest light sources on earth and are some of the most powerful tools available to X-ray crystallographers. X-ray beams are generated in large machines called synchrotrons which accelerate electrically charged particles, often electrons, to nearly the speed of light and confine them in a (roughly) circular loop using magnetic fields.

Synchrotrons are generally national facilities, each with several dedicated beamlines where data is collected without interruption. Synchrotrons were originally designed for use by high-energy physicists studying subatomic particles and cosmic phenomena. The largest component of each synchrotron is its electron storage ring. This ring is actually not a perfect circle, but a many-sided polygon. At each corner of the polygon, or sector, precisely aligned magnets bend the electron stream. As the electrons' path is bent, they emit bursts of energy in the form of X-rays.

Using synchrotron radiation frequently has specific requirements for X-ray crystallography. The intense ionizing radiation can cause radiation damage to samples, particularly macromolecular crystals. Cryo crystallography protects the sample from radiation damage, by freezing the crystal at liquid nitrogen temperatures (~100 K). Cryocrystallography methods are applied to home source rotating anode sources as well. However, synchrotron radiation frequently has the advantage of user-selectable wavelengths, allowing for anomalous scattering experiments which maximizes anomalous signal. This is critical in experiments such as single wavelength anomalous dispersion (SAD) and multi-wavelength anomalous dispersion (MAD).

Free-electron laser

Free-electron lasers have been developed for use in X-ray crystallography. These are the brightest X-ray sources currently available; with the X-rays coming in femtosecond bursts. The intensity of the source is such that atomic resolution diffraction patterns can be resolved for crystals otherwise too small for collection. However, the intense light source also destroys the sample, requiring multiple crystals to be shot. As each crystal is randomly oriented in the beam, hundreds of thousands of individual diffraction images must be collected in order to get a complete data set. This method, serial femtosecond crystallography, has been used in solving the structure of a number of protein crystal structures, sometimes noting differences with equivalent structures collected from synchrotron sources.

Introduction to x-ray diffraction theory

Basics

The incoming beam (coming from upper left) causes each scatterer to re-radiate a small portion of its intensity as a spherical wave. If scatterers are arranged symmetrically with a separation d, these spherical waves will be in sync (add constructively) only in directions where their path-length difference 2d sin θ equals an integer multiple of the wavelength λ. In that case, part of the incoming beam is deflected by an angle 2θ, producing a reflection spot in the diffraction pattern.

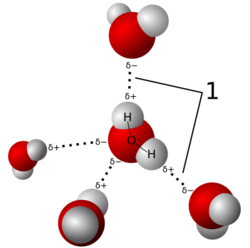
Crystals are regular arrays of atoms, and X-rays are electromagnetic waves. Atoms scatter X-ray waves, primarily through the atoms' electrons. Just as an ocean wave striking a lighthouse produces secondary circular waves emanating from the lighthouse, so an X-ray striking an electron produces secondary spherical waves emanating from the electron. This phenomenon is known as elastic scattering, and the electron (or lighthouse) is known as the scatterer. A regular array of scatterers produces a regular array of spherical waves. Although these waves cancel one another out in most directions through destructive interference, they add constructively in a few specific directions.

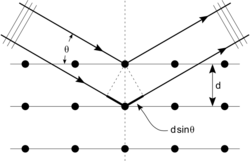
An intuitive understanding of X-ray diffraction can be obtained from the Bragg model of diffraction. In this model, a given reflection is associated with a set of evenly spaced sheets running through the crystal, usually passing through the centers of the atoms of the crystal lattice. The orientation of a particular set of sheets is identified by its three Miller indices (h, k, l), and their spacing by d. William Lawrence Bragg proposed a model in which the incoming X-rays are scattered specularly (mirror-like) from each plane; from that assumption, X-rays scattered from adjacent planes will combine constructively (constructive interference) when the angle θ between the plane and the X-ray results in a path-length difference that is an integer multiple n of the X-ray wavelength λ.

[math]\displaystyle{ 2 d\sin\theta = n\lambda. }[/math]

A reflection is said to be indexed when its Miller indices (or, more correctly, its reciprocal lattice vector components) have been identified from the known wavelength and the scattering angle 2θ. Such indexing gives the unit-cell parameters, the lengths and angles of the unit-cell, as well as its space group.

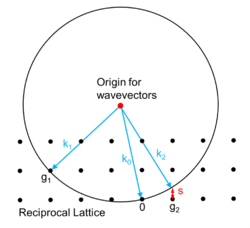
Ewald's sphere

Further information: Physics:Ewald's sphere

Representation of the Ewald construction for elastic diffraction of x-rays.

Each X-ray diffraction pattern represents a spherical slice of reciprocal space, as may be seen by the Ewald sphere construction. For a given incident wavevector k₀ the only wavevectors with the same energy lie on the surface of a sphere. In the diagram, the wavevector k₁ lies on the Ewald sphere and also is at a reciprocal lattice vector g₁ so satisfies Bragg's law. In contrast the wavevector k₂ differs from the reciprocal lattice point and g₂ by the vector s which is called the excitation error. For large single crystals primarily used in crystallography only the Bragg's law case matters; for electron diffraction and some other types of x-ray diffraction non-zero values of the excitation error also matter.

Scattering amplitudes

X-ray scattering is determined by the density of electrons within the crystal. Since the energy of an X-ray is much greater than that of a valence electron, the scattering may be modeled as Thomson scattering, the elastic interaction of an electromagnetic ray with a charged particle.

The intensity of Thomson scattering for one particle with mass m and elementary charge q is:

[math]\displaystyle{ I_o = I_e \left(\frac{q^4}{m^2c^4}\right)\frac{1+\cos^22\theta}{2} = I_e7.94\times10^{-26}\frac{1+\cos^22\theta}{2} = I_ef }[/math]

Hence the atomic nuclei, which are much heavier than an electron, contribute negligibly to the scattered X-rays. Consequently, the coherent scattering detected from an atom can be accurately approximated by analyzing the collective scattering from the electrons in the system.

The incoming X-ray beam has a polarization and should be represented as a vector wave; however, for simplicity, let it be represented here as a scalar wave. We also ignore the complication of the time dependence of the wave and just concentrate on the wave's spatial dependence. Plane waves can be represented by a wave vector k_in, and so the incoming wave at time t = 0 is given by

[math]\displaystyle{ A \mathrm{e}^{2\pi \mathrm{i}\mathbf{k}_{\mathrm{in}} \cdot \mathbf{r}}. }[/math]

At position r within the sample, let there be a density of scatterers f(r); these scatterers produce a scattered spherical wave of amplitude proportional to the local amplitude of the incoming wave times the number of scatterers in a small volume dV about r

[math]\displaystyle{ \text{amplitude of scattered wave} = A \mathrm{e}^{2\pi \mathrm{i}\mathbf{k} \cdot \mathbf{r}} S f(\mathbf{r}) \mathrm{d}V, }[/math]

where S is the proportionality constant.

Consider the fraction of scattered waves that leave with an outgoing wave-vector of k_out and strike a screen (detector) at r_screen. Since no energy is lost (elastic, not inelastic scattering), the wavelengths are the same as are the magnitudes of the wave-vectors |k_in|=|k_out|. From the time that the photon is scattered at r until it is absorbed at r_screen, the photon undergoes a change in phase

[math]\displaystyle{ e^{2\pi i \mathbf{k}_\text{out} \cdot \left( \mathbf{r}_\text{screen} - \mathbf{r} \right)}. }[/math]

The net radiation arriving at r_screen is the sum of all the scattered waves throughout the crystal

[math]\displaystyle{ A S \int \mathrm{d}\mathbf{r} f(\mathbf{r}) \mathrm{e}^{2\pi \mathrm{i} \mathbf{k}_\text{in} \cdot \mathbf{r}} e^{2\pi i \mathbf{k}_\text{out} \cdot \left( \mathbf{r}_\text{screen} - \mathbf{r} \right)} = A S e^{2\pi i \mathbf{k}_\text{out} \cdot \mathbf{r}_\text{screen}} \int \mathrm{d}\mathbf{r} f(\mathbf{r}) \mathrm{e}^{2\pi \mathrm{i} \left( \mathbf{k}_\text{in} - \mathbf{k}_\text{out} \right) \cdot \mathbf{r}}, }[/math]

which may be written as a Fourier transform

[math]\displaystyle{ A S \mathrm{e}^{2\pi \mathrm{i} \mathbf{k}_\text{out} \cdot \mathbf{r}_\text{screen}} \int d\mathbf{r} f(\mathbf{r}) \mathrm{e}^{-2\pi \mathrm{i} \mathbf{g} \cdot \mathbf{r}} = A S \mathrm{e}^{2\pi \mathrm{i} \mathbf{k}_\text{out} \cdot \mathbf{r}_\text{screen}} F(\mathbf{g}), }[/math]

where g = k_out – k_in is a reciprocal lattice vector that satisfies Bragg's law and the Ewald construction mentioned above. The measured intensity of the reflection will be square of this amplitude

[math]\displaystyle{ A^{2} S^{2} \left|F(\mathbf{g}) \right|^2. }[/math]

Related scattering techniques

Other X-ray techniques

Other forms of elastic X-ray scattering besides single-crystal diffraction include powder diffraction, small-angle X-ray scattering (SAXS) and several types of X-ray fiber diffraction, which was used by Rosalind Franklin in determining the double-helix structure of DNA. In general, single-crystal X-ray diffraction offers more structural information than these other techniques; however, it requires a sufficiently large and regular crystal, which is not always available.

These scattering methods generally use monochromatic X-rays, which are restricted to a single wavelength with minor deviations. A broad spectrum of X-rays (that is, a blend of X-rays with different wavelengths) can also be used to carry out X-ray diffraction, a technique known as the Laue method. This is the method used in the original discovery of X-ray diffraction. Laue scattering provides much structural information with only a short exposure to the X-ray beam, and is therefore used in structural studies of very rapid events (time resolved crystallography). However, it is not as well-suited as monochromatic scattering for determining the full atomic structure of a crystal and therefore works better with crystals with relatively simple atomic arrangements.

The Laue back reflection mode records X-rays scattered backwards from a broad spectrum source. This is useful if the sample is too thick for X-rays to transmit through it. The diffracting planes in the crystal are determined by knowing that the normal to the diffracting plane bisects the angle between the incident beam and the diffracted beam. A Greninger chart can be used to interpret the back reflection Laue photograph.

Electron diffraction

Because they interact via the Coulomb forces the scattering of electrons by matter is 1000 or more times stronger than for X-rays. Hence electron beams produce strong multiple or dynamical scattering even for relatively thin crystals (>10 nm). While there are similarities between the diffraction of X-rays and electrons, as can be found in the book by John M. Cowley, the approach is different as it is based upon the original approach of Hans Bethe and solving Schrödinger equation for relativistic electrons, rather than a kinematical or Bragg's law approach. Information about very small regions, down to single atoms is possible. The range of applications for electron diffraction, transmission electron microscopy and transmission electron crystallography with high energy electrons is extensive; see the relevant links for more information and citations. In addition to transmission methods, low-energy electron diffraction is a technique where electrons are back-scattered off surfaces and has been extensively used to determine surface structures at the atomic scale, and reflection high-energy electron diffraction is another which is extensively used to monitor thin film growth.

Neutron diffraction

Neutron diffraction is used for structure determination, although it has been difficult to obtain intense, monochromatic beams of neutrons in sufficient quantities. Traditionally, nuclear reactors have been used, although sources producing neutrons by spallation are becoming increasingly available. Being uncharged, neutrons scatter more from the atomic nuclei rather than from the electrons. Therefore, neutron scattering is useful for observing the positions of light atoms with few electrons, especially hydrogen, which is essentially invisible in X-ray diffraction. Neutron scattering also has the property that the solvent can be made invisible by adjusting the ratio of normal water, H₂O, and heavy water, D₂O.

Contribution of women to X-ray crystallography

A number of women were pioneers in X-ray crystallography at a time when they were excluded from most other branches of physical science.

Kathleen Lonsdale was a research student of William Henry Bragg, who had 11 women research students out of a total of 18. She is known for both her experimental and theoretical work. Lonsdale joined his crystallography research team at the Royal Institution in London in 1923, and after getting married and having children, went back to work with Bragg as a researcher. She confirmed the structure of the benzene ring, carried out studies of diamond, was one of the first two women to be elected to the Royal Society in 1945, and in 1949 was appointed the first female tenured professor of chemistry and head of the Department of crystallography at University College London. Lonsdale always advocated greater participation of women in science and said in 1970: "Any country that wants to make full use of all its potential scientists and technologists could do so, but it must not expect to get the women quite so simply as it gets the men. ... It is utopian, then, to suggest that any country that really wants married women to return to a scientific career, when her children no longer need her physical presence, should make special arrangements to encourage her to do so?". During this period, Lonsdale began a collaboration with William T. Astbury on a set of 230 space group tables which was published in 1924 and became an essential tool for crystallographers.

Molecular model of penicillin by Dorothy Hodgkin, 1945

In 1932 Dorothy Hodgkin joined the laboratory of the physicist John Desmond Bernal, who was a former student of Bragg, in Cambridge, UK. She and Bernal took the first X-ray photographs of crystalline proteins. Hodgkin also played a role in the foundation of the International Union of Crystallography. She was awarded the Nobel Prize in Chemistry in 1964 for her work using X-ray techniques to study the structures of penicillin, insulin and vitamin B12. Her work on penicillin began in 1942 during the war and on vitamin B12 in 1948. While her group slowly grew, their predominant focus was on the X-ray analysis of natural products. She is the only British woman ever to have won a Nobel Prize in a science subject.

Photograph of DNA (photo 51), Rosalind Franklin, 1952

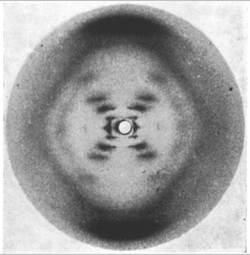
Rosalind Franklin took the X-ray photograph of a DNA fibre that proved key to James Watson and Francis Crick's discovery of the double helix, for which they both won the Nobel Prize for Physiology or Medicine in 1962. Watson revealed in his autobiographic account of the discovery of the structure of DNA, The Double Helix, that he had used Franklin's X-ray photograph without her permission. Franklin died of cancer in her 30s, before Watson received the Nobel Prize. Franklin also carried out important structural studies of carbon in coal and graphite, and of plant and animal viruses.

Isabella Karle of the United States Naval Research Laboratory developed an experimental approach to the mathematical theory of crystallography. Her work improved the speed and accuracy of chemical and biomedical analysis. Yet only her husband Jerome shared the 1985 Nobel Prize in Chemistry with Herbert Hauptman, "for outstanding achievements in the development of direct methods for the determination of crystal structures". Other prize-giving bodies have showered Isabella with awards in her own right.

Women have written many textbooks and research papers in the field of X-ray crystallography. For many years Lonsdale edited the International Tables for Crystallography, which provide information on crystal lattices, symmetry, and space groups, as well as mathematical, physical and chemical data on structures. Olga Kennard of the University of Cambridge, founded and ran the Cambridge Crystallographic Data Centre, an internationally recognized source of structural data on small molecules, from 1965 until 1997. Jenny Pickworth Glusker, a British scientist, co-authored Crystal Structure Analysis: A Primer, first published in 1971 and as of 2010 in its third edition. Eleanor Dodson, an Australian-born biologist, who began as Dorothy Hodgkin's technician, was the main instigator behind CCP4, the collaborative computing project that currently shares more than 250 software tools with protein crystallographers worldwide.

Nobel Prizes involving X-ray crystallography

Year	Laureate	Prize	Rationale
1914	Max von Laue	Physics	"For his discovery of the diffraction of X-rays by crystals"
1915	William Henry Bragg	Physics	"For their services in the analysis of crystal structure by means of X-rays"
	William Lawrence Bragg
1962	Max F. Perutz	Chemistry	"for their studies of the structures of globular proteins"
	John C. Kendrew
1962	James Dewey Watson	Medicine	"For their discoveries concerning the molecular structure of nucleic acids and its significance for information transfer in living material"
	Francis Harry Compton Crick
	Maurice Hugh Frederick Wilkins
1964	Dorothy Hodgkin	Chemistry	"For her determinations by X-ray techniques of the structures of important biochemical substances"
1972	Stanford Moore	Chemistry	"For their contribution to the understanding of the connection between chemical structure and catalytic activity of the active centre of the ribonuclease molecule"
	William H. Stein
1976	William N. Lipscomb	Chemistry	"For his studies on the structure of boranes illuminating problems of chemical bonding"
1985	Jerome Karle	Chemistry	"For their outstanding achievements in developing direct methods for the determination of crystal structures"
	Herbert A. Hauptman
1988	Johann Deisenhofer	Chemistry	"For their determination of the three-dimensional structure of a photosynthetic reaction centre"
	Hartmut Michel	Chemistry
	Robert Huber	Chemistry
1997	John E. Walker	Chemistry	"For their elucidation of the enzymatic mechanism underlying the synthesis of adenosine triphosphate (ATP)"
2003	Roderick MacKinnon	Chemistry	"For discoveries concerning channels in cell membranes [...] for structural and mechanistic studies of ion channels"
	Peter Agre		"For discoveries concerning channels in cell membranes [...] for the discovery of water channels"
2006	Roger D. Kornberg	Chemistry	"For his studies of the molecular basis of eukaryotic transcription"
2009	Ada E. Yonath	Chemistry	"For studies of the structure and function of the ribosome"
	Thomas A. Steitz
	Venkatraman Ramakrishnan
2012	Brian Kobilka	Chemistry	"For studies of G-protein-coupled receptors"

See also

• Beevers–Lipson strip
• Bragg diffraction
• Crystallographic database
• Crystallographic point groups
• Difference density map
• Electron diffraction
• Energy-dispersive X-ray diffraction
• Flack parameter
• Grazing incidence diffraction
• Henderson limit
• International Year of Crystallography
• Multipole density formalism
• Neutron diffraction
• Powder diffraction
• Ptychography
• Scherrer equation
• Small angle X-ray scattering (SAXS)
• Structure determination
• Ultrafast x-ray
• Wide angle X-ray scattering (WAXS)

Further reading

International Tables for Crystallography

• International Tables for Crystallography. Volume A, Space-group Symmetry (5th ed.). Dordrecht: Kluwer Academic Publishers, for the International Union of Crystallography. 2002. ISBN 0-7923-6590-9. 
• International Tables for Crystallography. Volume F, Crystallography of biological molecules. Dordrecht: Kluwer Academic Publishers, for the International Union of Crystallography. 2001. ISBN 0-7923-6857-6. 
• International Tables for Crystallography. Brief Teaching Edition of Volume A, Space-group Symmetry (4th ed.). Dordrecht: Kluwer Academic Publishers, for the International Union of Crystallography. 1996. ISBN 0-7923-4252-6. 

Bound collections of articles

• Macromolecular Crystallography, Part A (Methods in Enzymology, v. 276). San Diego: Academic Press. 1997. ISBN 0-12-182177-3. https://archive.org/details/macromolecularcr0000unse. 
• Macromolecular Crystallography, Part B (Methods in Enzymology, v. 277). San Diego: Academic Press. 1997. ISBN 0-12-182178-1. 
• Crystallization of Nucleic Acids and Proteins: A Practical Approach (2nd ed.). Oxford: Oxford University Press. 1999. ISBN 0-19-963678-8. 

Textbooks

• "Chapter 1: Principles_of_X-ray_Diffraction". Thin Film Analysis by X-Ray Scattering. Weinheim: Wiley-VCH. 2005. ISBN 978-3-527-31052-4. https://www.researchgate.net/publication/260086423. 
• Outline of Crystallography for Biologists. Oxford: Oxford University Press. 2002. ISBN 0-19-851051-9. 
• Space Groups for Scientists and Engineers (2nd ed.). Boston: Academic Press, Inc.. 1990. ISBN 0-12-145761-3. https://archive.org/details/spacegroupsforso0000burn. 
• Crystal Structure Determination (Oxford Chemistry Primer). Oxford: Oxford University Press. 1998. ISBN 0-19-855901-1. 
• Elements of X-Ray Diffraction (2nd ed.). Reading, Massachusetts: Addison-Wesley Publishing Company. 1978. ISBN 0-534-55396-6. 
• Principles of Protein X-Ray Crystallography. New York: Springer-Verlag. 1999. ISBN 0-387-98587-5. 
• Fundamentals of Crystallography. Oxford: Oxford University Press. 1992. ISBN 0-19-855578-4. 
• Crystal Structure Analysis for Chemists and Biologists. New York: VCH Publishers. 1994. ISBN 0-471-18543-4. 
• Crystal Structure Determination. Berlin: Springer. 2004. ISBN 3-540-20644-2. 
• Crystallization of Biological Macromolecules. Cold Spring Harbor, NY: Cold Spring Harbor Laboratory Press. 1999. ISBN 0-87969-617-6. 
• Introduction to Macromolecular Crystallography. John Wiley & Sons. 2003. ISBN 0-471-25122-4. 
• Practical Protein Crystallography. San Diego: Academic Press. 1993. ISBN 0-12-486050-8. https://archive.org/details/practicalprotein00mcre_0. 
• Crystal Structures; I. Patterns and Symmetry. Washington, DC: Mineralogical Society of America, Monograph Series. 1996. ISBN 0-939950-40-5. 
• Crystallography Made Crystal Clear. San Diego: Academic Press. 2000. ISBN 0-12-587072-8. , PDF copy of select chapters
• Biomolecular Crystallography: Principles, Practice and Application to Structural Biology. New York: Garland Science. 2009. ISBN 978-0-8153-4081-2. 
• X-ray Diffraction. New York. 1969. ISBN 0-486-66317-5. 
• Theory of X-ray Diffraction in Crystals. New York: Dover Publications. 1945. 

Applied computational data analysis

• The Rietveld Method. Oxford: Oxford University Press & International Union of Crystallography. 1993. ISBN 0-19-855577-6. 

Historical

• Early Papers on Diffraction of X-rays by Crystals. I. Utrecht: published for the International Union of Crystallography by A. Oosthoek's Uitgeversmaatschappij N.V.. 1969. 
• Early Papers on Diffraction of X-rays by Crystals. II. Utrecht: published for the International Union of Crystallography by A. Oosthoek's Uitgeversmaatschappij N.V.. 1972. 
• The Development of X-ray Analysis. New York: Dover. 1992. ISBN 0-486-67316-2. https://archive.org/details/developmentofxra00brag_0. 
• Fifty Years of X-ray Diffraction. Utrecht: published for the International Union of Crystallography by A. Oosthoek's Uitgeversmaatschappij N.V.. 1962. doi:10.1007/978-1-4615-9961-6. ISBN 978-1-4615-9963-0. 
• "50 Years of X-Ray Diffraction". International Union of Crystallography. http://www.iucr.org/iucr-top/publ/50YearsOfXrayDiffraction/. "Reprinted in pdf format for the IUCr XVIII Congress, Glasgow, Scotland" 
• "Die Geschichte der Auffindung der Röntgenstrahlinterferenzen". Die Naturwissenschaften 10 (16): 363. 1922. doi:10.1007/BF01565289. Bibcode: 1922NW.....10..363F. https://zenodo.org/record/2307864. 
• Crystals and X-rays. New York: D. van Nostrand. 1949. 

External links

Tutorials

• Learning Crystallography
• Simple, non technical introduction
• The Crystallography Collection, video series from the Royal Institution
• "Small Molecule Crystalization" (PDF) at Illinois Institute of Technology website
• International Union of Crystallography
• Crystallography 101
• Interactive structure factor tutorial, demonstrating properties of the diffraction pattern of a 2D crystal.
• Picturebook of Fourier Transforms, illustrating the relationship between crystal and diffraction pattern in 2D.
• Lecture notes on X-ray crystallography and structure determination
• Online lecture on Modern X-ray Scattering Methods for Nanoscale Materials Analysis by Richard J. Matyi
• Interactive Crystallography Timeline from the Royal Institution

Primary databases

• Crystallography Open Database (COD)
• Protein Data Bank (PDB)
• Nucleic Acid Databank (NDB)
• Cambridge Structural Database (CSD)
• Inorganic Crystal Structure Database (ICSD)
• Biological Macromolecule Crystallization Database (BMCD)

Derivative databases

• PDBsum
• Proteopedia – the collaborative, 3D encyclopedia of proteins and other molecules
• RNABase
• HIC-Up database of PDB ligands
• Structural Classification of Proteins database
• CATH Protein Structure Classification
• List of transmembrane proteins with known 3D structure
• Orientations of Proteins in Membranes database

Structural validation

• MolProbity structural validation suite
• ProSA-web
• NQ-Flipper (check for unfavorable rotamers of Asn and Gln residues)
• DALI server (identifies proteins similar to a given protein)