Biology:Isothermal titration calorimetry

From HandWiki
Isothermal Titration Calorimetry
AcronymITC
ClassificationThermal analysis
ManufacturersTA Instruments, Microcal/Malvern Instruments
Other techniques
RelatedIsothermal microcalorimetry
Differential scanning calorimetry
MicroCal. VP-ITC in a glove box.

In chemical thermodynamics, isothermal titration calorimetry (ITC) is a physical technique used to determine the thermodynamic parameters of interactions in solution.[1][2] It is most often used to study the binding of small molecules (such as medicinal compounds) to larger macromolecules (proteins, DNA etc.) in a label-free environment.[3][4] It consists of two cells which are enclosed in an adiabatic jacket. The compounds to be studied are placed in the sample cell, while the other cell, the reference cell, is used as a control and contains the buffer in which the sample is dissolved.

The technique was developed by H. D. Johnston in 1968 as a part of his Ph.D. dissertation at Brigham Young University,[5] and was considered niche until introduced commercially by MicroCal Inc. in 1988. Compared to other calorimeters, ITC has an advantage in not requiring any correctors since there was no heat exchange between the system and the environment.

Thermodynamic measurements

ITC thermogram

ITC is a quantitative technique that can determine the binding affinity ([math]\displaystyle{ K_a }[/math]), enthalpy changes ([math]\displaystyle{ \Delta H }[/math]), and binding stoichiometry ([math]\displaystyle{ n }[/math]) of the interaction between two or more molecules in solution. This is achieved from integrating the area of the injection peaks and plotting the individual values by molar ratio of the binding event versus [math]\ce{ \Delta H }[/math] (kcal/mol). From these initial measurements, Gibbs free energy changes ([math]\displaystyle{ \Delta G }[/math]) and entropy changes ([math]\displaystyle{ \Delta S }[/math]) can be determined using the relationship:

[math]\displaystyle{ \Delta G = -RT\ln{K_a} = \Delta H -T\Delta S }[/math]

(where [math]\displaystyle{ R }[/math] is the gas constant and [math]\displaystyle{ T }[/math] is the absolute temperature).

For accurate measurements of binding affinity, the curve of the thermogram must be sigmoidal. The profile of the curve is determined by the c-value, which is calculated using the equation:

[math]\displaystyle{ c = n K_a M }[/math]

where [math]\displaystyle{ n }[/math] is the stoichiometry of the binding, [math]\displaystyle{ K_a }[/math] is the association constant and [math]\displaystyle{ M }[/math] is the concentration of the molecule in the cell.[1][6][7] The c-value must fall between 1 and 1000, ideally between 10 and 100. In terms of binding affinity, it would be approximately from [math]\displaystyle{ 1.0 \times 10^3 }[/math] ~ [math]\displaystyle{ 10^7 }[/math]within the limit range.[8]

Instrumental measurements

Schematic of an ITC instrument

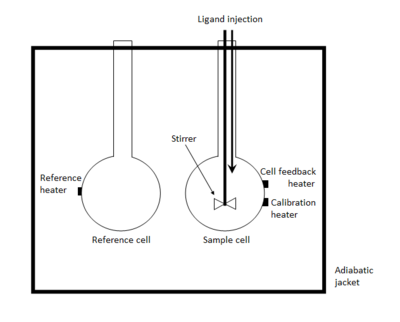
An isothermal titration calorimeter is composed of two identical cells made of a highly efficient thermally conducting and chemically inert material such as Hastelloy alloy or gold, surrounded by an adiabatic jacket.[1][7] Sensitive thermopile/thermocouple circuits are used to detect temperature differences between the reference cell (filled with buffer or water) and the sample cell containing the macromolecule. Prior to addition of ligand, a constant power (<1 mW) is applied to the reference cell. This directs a feedback circuit, activating a heater located on the sample cell.[6] During the experiment, ligand is titrated into the sample cell in precisely known aliquots, causing heat to be either taken up or evolved (depending on the nature of the reaction). Measurements consist of the time-dependent input of power required to maintain equal temperatures between the sample and reference cells.[5]

In an exothermic reaction, the temperature in the sample cell increases upon addition of ligand. This causes the feedback power to the sample cell to be decreased (remember: a reference power is applied to the reference cell) in order to maintain an equal temperature between the two cells. In an endothermic reaction, the opposite occurs; the feedback circuit increases the power in order to maintain a constant temperature (isothermal operation).[1]

Observations are plotted as the power needed to maintain the reference and the sample cell at an identical temperature against time. As a result, the experimental raw data consists of a series of spikes of heat flow (power), with every spike corresponding to one ligand injection. These heat flow spikes/pulses are integrated with respect to time, giving the total heat exchanged per injection. The pattern of these heat effects as a function of the molar ratio [ligand]/[macromolecule] can then be analyzed to give the thermodynamic parameters of the interaction under study.

To obtain an optimum result, each injection should be given enough time for a reaction equilibrium to reach. Degassing samples is often necessary in order to obtain good measurements as the presence of gas bubbles within the sample cell will lead to abnormal data plots in the recorded results. The entire experiment takes place under computer control.[7]

Direct titration is performed most commonly with ITC to obtain the thermodynamic data, by binding two components of the reaction directly to each other. However, many of the chemical reactions and binding interactions may have higher binding affinity above what is desirable with the c-window. To troubleshoot the limitation of c-window and conditions for certain binding interactions, various different methods of titration can be performed. In some cases, simply doing a reverse titration of changing the samples between the injection syringe and sample cell can solve the issue, depending on the binding mechanism.[9] For most of the high or low affinity bindings require chelation or competitive titration. This method is done by loading pre-bound complex solution in the sample cell, and chelating one of the components out with a reagent of higher observed binding affinity within the desirable c-window.

Analysis and interpretation

Post-hoc analysis and proton inventory

The collected experimental data reflects not only the binding thermodynamics of the interaction of interest, but any contributing competing equilibria associated to it. A post-hoc analysis can be performed to determine the buffer or solvent-independent enthalpy from the experimental thermodynamics, by simply going through the process of Hess’ law. Below example shows a simple interaction between a metal ion (M) and a ligand (L). B represents the buffer used for this interaction and [math]\ce{ H+ }[/math] represents protons.

[math]\ce{ M - B <=> M + B }[/math] [math]\ce{ -\Delta H_{MB} }[/math]

[math]\ce{ L - H <=> L + H+ }[/math] [math]\displaystyle{ - (n_{H+}) \Delta H_{LH} }[/math]

[math]\ce{ H+ + B <=> H - B }[/math] [math]\displaystyle{ (n_{H+}) \Delta H_{BH} }[/math]

[math]\ce{ M + L <=> M - L }[/math] [math]\displaystyle{ \Delta H_{ML} }[/math]

An example of a proton inventory plot of a binding interaction. Averaged enthalpic values gathered under three different buffer conditions(TAPSO, bis-Tris, and HEPES) are presented. X- and Y-axis are buffer protonation enthalpy and observed enthalpy from conducted experiments.

Therefore,

[math]\displaystyle{ \Delta H_{ITC} = -\Delta H_{MB} - (n_{H+}) \Delta H_{LH} + (n_{H+}) \Delta H_{BH} + \Delta H_{ML} }[/math]

which can be further processed to calculate the enthalpy of metal-ligand interaction.[10][11] Although this example is between a metal and a ligand, it is applicable to any ITC experiment, regarding binding interactions.

As a part of the analysis, a number of protons are required to calculate the solvent-independent thermodynamics. This can be easily done by plotting a graph such as shown below.

The linear equation of this plot is the rearranged version of the equation above from the post-hoc analysis in a form of y = mx + b:

[math]\displaystyle{ \Delta H_{ITC} = (n_{H+}) \Delta H_{BH} + [ -\Delta H_{MB} - (n_{H+}) \Delta H_{LH} + \Delta H_{ML} ] }[/math]

Equilibrium constant

Equilibrium constant of the reaction is also not independent from the other competing equilibria. Competition would include buffer interactions and other pH-dependent reactions depending on the experimental conditions. The competition from species other than the species of interest is included in the competition factor, Q in the following equation:[11]

[math]\displaystyle{ Q = \Sigma (\beta _n [\Chi ]_n) }[/math]

where, [math]\displaystyle{ X }[/math] represents species such a buffer or protons, [math]\displaystyle{ \beta }[/math] represents their equilibrium constant, when,

[math]\displaystyle{ K_{ML} = K_{ITC} Q }[/math]

Applications

For the past 30 years, isothermal titration calorimetry has been used in a wide array of fields. In the old days, this technique was used to determine fundamental thermodynamic values for basic small molecular interactions.[12] In recent years, ITC has been used in more industrially applicable areas, such as drug discovery and testing synthetic materials. Although it is still heavily used in fundamental chemistry, the trend has shifted over to the biological side, where label-free and buffer independent values are relatively harder to achieve.[13][14]

Enzyme kinetics

Using the thermodynamic data from ITC, it is possible to deduce enzyme kinetics including proton or electron transfer, allostery and cooperativity, and enzyme inhibition.[15][16] ITC collects data over time that is useful for any kinetic experiments, but especially with the proteins due to constant aliquots of injections. In terms of calculation, equilibrium constant and the slopes of binding can be directly utilized to determine the allostery and charge transfer, by comparing experimental data of different conditions (pH, use of mutated peptide chain and binding sites, etc.) .

Membrane and self-assembling peptide studies

Membrane proteins and self-assembly properties of certain proteins can be studied under this technique, due to being a label-free calorimeter. Membrane proteins are known to have difficulties with selection of proper solubilization and purification protocols. As ITC is a non-destructive calorimetric tool, it can be used as a detector to locate the fraction of protein with desired binding sites, by binding a known binding ligand to the protein.[17] This feature also applies in studies of self-assembling proteins, especially in use of measuring thermodynamics of their structural transformation.[18]

Drug development

Binding affinity carries a huge importance in medicinal chemistry, as drugs need to bind to the protein effectively within a desired range. However, determining enthalpy changes and optimization of thermodynamic parameters are hugely difficult when designing drugs.[19] ITC troubleshoots this issue easily by deducing the binding affinity, enthalpic/entropic contributions and its binding stoichiometry.

Chiral chemistry

Applying the ideas above, chirality of organometallic compounds can be deduced as well with this technique.[20] Each chiral compound has its own unique properties and binding mechanisms that are comparable to each other, which leads to differences in thermodynamic properties. By binding chiral solutions in a binding site can deduce the type of chirality and depending on the purpose, which chiral compound is more suitable for binding.

Metal binding interactions

Binding metal ions to protein and other components of biological material is one of the most popular uses of ITC, since ovotransferrin to ferric iron binding study published by Lin et al. from MicroCal Inc.[21] This is due to some of the metal ions utilized in biological systems having d10 electron configuration which cannot be studied with other common techniques such as UV-vis spectrophotometry or electron paramagnetic resonance.[8][10] It is also closely related to biochemical and medicinal studies due to the large abundance of metal binding enzymes in biological systems.[22]

Carbon nanotubes and related materials

The technique has been well utilized in studying carbon nanotubes to determine thermodynamic binding interactions with biological molecules and graphene composite interactions.[23] Another notable use of ITC with carbon nanotubes is optimization of preparation of carbon nanotubes from graphene composite and polyvinyl alcohol (PVA). PVA assembly process can be measured thermodynamically as mixing of the two ingredients is an exothermic reaction, and its binding trend can be easily observed by ITC.

See also

References

  1. ↑ 1.0 1.1 1.2 1.3 Freire, Ernesto; Mayorga, Obdulio L.; Straume, Martin (1990-09-01). "Isothermal titration calorimetry" (in en). Analytical Chemistry 62 (18): 950A–959A. doi:10.1021/ac00217a002. ISSN 0003-2700. https://pubs.acs.org/doi/abs/10.1021/ac00217a002. 
  2. ↑ Grolier, Jean-Pierre E.; del Río, José Manuel (2012). "Isothermal titration calorimetry: A thermodynamic interpretation of measurements" (in en). The Journal of Chemical Thermodynamics 55: 193–202. doi:10.1016/j.jct.2012.05.018. https://linkinghub.elsevier.com/retrieve/pii/S0021961412002078. 
  3. ↑ Serdyuk; Zaccai; Zaccai (2017). "Chapter C3 Isothermal Titration Calorimetry". Methods in molecular biophysics: Structure, dynamics, function. Cambridge University Press. pp. 221–233. 
  4. ↑ Kuriyan; Conforti; Wemmer (2013). "12.23 Isothermal titration calorimetry allows us to determine the enthalpic and entropic components of the binding free energy.". The molecules of life: Physical and chemical principles. Garland Publishing.. pp. 573–577. 
  5. ↑ 5.0 5.1 Johnston, H. D. (1968) The thermodynamics (log K, ΔH°, ΔS°, ΔCp°) of metal ligand interaction in aqueous solution. Brigham Young University.
  6. ↑ 6.0 6.1 Quick Start: Isothermal Titration Calorimetry (ITC) (2016). TA Instrument. New Castle, DE.
  7. ↑ 7.0 7.1 7.2 VP-ITC Instruction Manual (2001). Microcal Inc., Northampton, MA.
  8. ↑ 8.0 8.1 Stevenson, M. J. (2016) Thermodynamic studies of Cu(I) and other d10 metal ions binding to proteins in the copper homeostasis pathway and the organomercurial detoxification pathway. Dartmouth College.
  9. ↑ Grolier, Jean-Pierre E.; del Río, Jose Manuel (2015). "Isothermal Titration Calorimetry: Application of the Gibbs–Duhem Equation to the Study of the Relationship Between Forward and Reverse Titrations" (in en). Journal of Solution Chemistry 44 (5): 987–1003. doi:10.1007/s10953-014-0243-7. ISSN 0095-9782. http://link.springer.com/10.1007/s10953-014-0243-7. 
  10. ↑ 10.0 10.1 Grossoehme, Nicholas E.; Spuches, Anne M.; Wilcox, Dean E. (2010). "Application of isothermal titration calorimetry in bioinorganic chemistry" (in en). Journal of Biological Inorganic Chemistry 15 (8): 1183–1191. doi:10.1007/s00775-010-0693-3. ISSN 0949-8257. PMID 20725755. http://link.springer.com/10.1007/s00775-010-0693-3. 
  11. ↑ 11.0 11.1 Quinn, Colette F.; Carpenter, Margaret C.; Croteau, Molly L.; Wilcox, Dean E. (2016) (in en), Isothermal Titration Calorimetry Measurements of Metal Ions Binding to Proteins, Methods in Enzymology, 567, Elsevier, pp. 3–21, doi:10.1016/bs.mie.2015.08.021, ISBN 978-0-12-802906-0, PMID 26794348, https://linkinghub.elsevier.com/retrieve/pii/S0076687915004887, retrieved 2023-02-15 
  12. ↑ Parrish, Wm.R. (1986). "Recent Advances in Calorimetry" (in en). Fluid Phase Equilibria 29: 177–192. doi:10.1016/0378-3812(86)85020-8. https://linkinghub.elsevier.com/retrieve/pii/0378381286850208. 
  13. ↑ Falconer, Robert J. (2016). "Applications of isothermal titration calorimetry - the research and technical developments from 2011 to 2015: Review of Isothermal Titration Calorimetry from 2011 to 2015" (in en). Journal of Molecular Recognition 29 (10): 504–515. doi:10.1002/jmr.2550. PMID 27221459. https://onlinelibrary.wiley.com/doi/10.1002/jmr.2550. 
  14. ↑ Falconer, Robert J.; Schuur, Boelo; Mittermaier, Anthony K. (2021). "Applications of isothermal titration calorimetry in pure and applied research from 2016 to 2020" (in en). Journal of Molecular Recognition 34 (10): e2901. doi:10.1002/jmr.2901. ISSN 0952-3499. PMID 33975380. https://onlinelibrary.wiley.com/doi/10.1002/jmr.2901. 
  15. ↑ Wang, Yun; Wang, Guanyu; Moitessier, Nicolas; Mittermaier, Anthony K. (2020-10-19). "Enzyme Kinetics by Isothermal Titration Calorimetry: Allostery, Inhibition, and Dynamics". Frontiers in Molecular Biosciences 7: 583826. doi:10.3389/fmolb.2020.583826. ISSN 2296-889X. PMID 33195429. 
  16. ↑ Burnouf, Dominique; Ennifar, Eric; Guedich, Sondes; Puffer, Barbara; Hoffmann, Guillaume; Bec, Guillaume; Disdier, François; Baltzinger, Mireille et al. (2012-01-11). "kinITC: A New Method for Obtaining Joint Thermodynamic and Kinetic Data by Isothermal Titration Calorimetry" (in en). Journal of the American Chemical Society 134 (1): 559–565. doi:10.1021/ja209057d. ISSN 0002-7863. PMID 22126339. https://pubs.acs.org/doi/10.1021/ja209057d. 
  17. ↑ Draczkowski, Piotr; Matosiuk, Dariusz; Jozwiak, Krzysztof (2014). "Isothermal titration calorimetry in membrane protein research" (in en). Journal of Pharmaceutical and Biomedical Analysis 87: 313–325. doi:10.1016/j.jpba.2013.09.003. PMID 24119484. https://linkinghub.elsevier.com/retrieve/pii/S0731708513004287. 
  18. ↑ Kabiri, M., & Unsworth, L. D. (2014). Application of isothermal titration calorimetry for characterizing thermodynamic parameters of biomolecular interactions: peptide self-assembly and protein adsorption case studies. Biomacromolecules, 15(10), 3463–3473. doi:10.1021/bm5004515
  19. ↑ Freire, Ernesto (2008-10-01). "Do enthalpy and entropy distinguish first in class from best in class?" (in en). Drug Discovery Today 13 (19): 869–874. doi:10.1016/j.drudis.2008.07.005. ISSN 1359-6446. PMID 18703160. 
  20. ↑ Werber, L., & Mastai, Y. (2018). Isothermal titration calorimetry for chiral chemistry. Chirality, 30(5), 619–631. doi:10.1002/chir.22842
  21. ↑ Lin, L. N., Mason, A. B., Woodworth, R. C., & Brandts, J. F. (1991). Calorimetric studies of the binding of ferric ions to ovotransferrin and interactions between binding sites. Biochemistry, 30(50), 11660–11669. doi:10.1021/bi00114a008
  22. ↑ Faller, P., Hureau, C., Dorlet, P., Hellwig, P., Coppel, Y., Collin, F., & Alies, B. (2012). Methods and techniques to study the bioinorganic chemistry of metal–peptide complexes linked to neurodegenerative diseases. Coordination Chemistry Reviews, 256(19–20), 2381–2396. doi:10.1016/j.ccr.2012.03.015
  23. ↑ Rodríguez-Estupiñán, P., Miranda-Carvajal, I., Campos, P. C., Guerrero-Fajardo, C. A., Giraldo, L., & Moreno-Piraján, J. C. (2022). Graphene-based materials: analysis through calorimetric techniques. Journal of Thermal Analysis and Calorimetry, 147(17), 9301–9351. doi:10.1007/s10973-022-11206-w



Retrieved from "https://handwiki.org/wiki/index.php?title=Biology:Isothermal_titration_calorimetry&oldid=3549934"