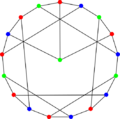
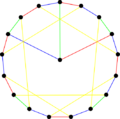
Blanuša snarks
| Blanuša snarks | |
|---|---|
 The first Blanuša snark | |
| Named after | Danilo Blanuša |
| Vertices | 18 (both) |
| Edges | 27 (both) |
| Radius | 4 (both) |
| Diameter | 4 (both) |
| Girth | 5 (both) |
| Automorphisms | 8, D4 (1st) 4, Klein group (2nd) |
| Chromatic number | 3 (both) |
| Chromatic index | 4 (both) |
| Book thickness | 3 (both) |
| Queue number | 2 (both) |
| Table of graphs and parameters | |
In the mathematical field of graph theory, the Blanuša snarks are two 3-regular graphs with 18 vertices and 27 edges.[1] They were discovered by Yugoslavian mathematician Danilo Blanuša in 1946 and are named after him.[2] When discovered, only one snark was known—the Petersen graph.
As snarks, the Blanuša snarks are connected, bridgeless cubic graphs with chromatic index equal to 4. Both of them have chromatic number 3, diameter 4 and girth 5. They are non-hamiltonian but are hypohamiltonian.[3] Both have book thickness 3 and queue number 2.[4]
Algebraic properties
The automorphism group of the first Blanuša snark is of order 8 and is isomorphic to the Dihedral group D4, the group of symmetries of a square.
The automorphism group of the second Blanuša snark is an abelian group of order 4 isomorphic to the Klein four-group, the direct product of the Cyclic group Z/2Z with itself.
The characteristic polynomial of the first and the second Blanuša snark are respectively :
- [math]\displaystyle{ (x-3)(x-1)^3(x+1)(x+2)(x^4+x^3-7x^2-5x+6)(x^4+x^3-5x^2-3x+4)^2\ }[/math]
- [math]\displaystyle{ (x-3)(x-1)^3(x^3+2x^2-3x-5)(x^3+2x^2-x-1)(x^4+x^3-7x^2-6x+7)(x^4+x^3-5x^2-4x+3).\ }[/math]
Generalized Blanuša snarks
There exists a generalisation of the first and second Blanuša snark in two infinite families of snarks of order 8n+10 denoted [math]\displaystyle{ B_n^1 }[/math] and [math]\displaystyle{ B_n^2 }[/math]. The Blanuša snarks are the smallest members those two infinite families.[5]
In 2007, J. Mazák proved that the circular chromatic index of the type 1 generalized Blanuša snarks [math]\displaystyle{ B_n^1 }[/math] equals [math]\displaystyle{ 3+{\frac {2} {n}} }[/math].[6]
In 2008, M. Ghebleh proved that the circular chromatic index of the type 2 generalized Blanuša snarks [math]\displaystyle{ B_n^2 }[/math] equals [math]\displaystyle{ 3+{\frac {1} {\lfloor 1+3n/2\rfloor}} }[/math].[7]
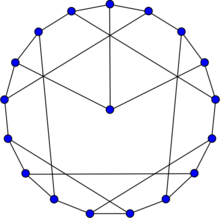
Gallery
The chromatic number of the first Blanuša snark is 3.
The chromatic index of the first Blanuša snark is 4.
The chromatic number of the second Blanuša snark is 3.
The chromatic index of the second Blanuša snark is 4.
References
- ↑ Weisstein, Eric W.. "Blanuša snarks". http://mathworld.wolfram.com/BlanusaSnarks.html.
- ↑ Blanuša, D., "Problem cetiriju boja." Glasnik Mat. Fiz. Astr. Ser. II. 1, 31-42, 1946.
- ↑ Eckhard Steen, "On Bicritical Snarks" Math. Slovaca, 1997.
- ↑ Wolz, Jessica; Engineering Linear Layouts with SAT. Master Thesis, University of Tübingen, 2018
- ↑ Read, R. C. and Wilson, R. J. An Atlas of Graphs. Oxford, England: Oxford University Press, pp. 276 and 280, 1998.
- ↑ J. Mazák, Circular chromatic index of snarks, Master's thesis, Comenius University in Bratislava, 2007.
- ↑ M. Ghebleh, Circular Chromatic Index of Generalized Blanuša Snarks, The Electronic Journal of Combinatorics, vol 15, 2008.
 |  |
