Braess's paradox
Braess's paradox is the observation that adding one or more roads to a road network can slow down overall traffic flow through it. The paradox was first discovered by Arthur Pigou in 1920,[1] and later named after the German mathematician Dietrich Braess in 1968.[2]
The paradox may have analogies in electrical power grids and biological systems. It has been suggested that, in theory, the improvement of a malfunctioning network could be accomplished by removing certain parts of it. The paradox has been used to explain instances of improved traffic flow when existing major roads are closed.
Discovery and definition
Dietrich Braess, a mathematician at Ruhr University, Germany , noticed the flow in a road network could be impeded by adding a new road, when he was working on traffic modelling. His idea was that if each driver is making the optimal self-interested decision as to which route is quickest, a shortcut could be chosen too often for drivers to have the shortest travel times possible. More formally, the idea behind Braess's discovery is that the Nash equilibrium may not equate with the best overall flow through a network.[3]
The paradox is stated as follows:
"For each point of a road network, let there be given the number of cars starting from it and the destination of the cars. Under these conditions, one wishes to estimate the distribution of traffic flow. Whether one street is preferable to another depends not only on the quality of the road, but also on the density of the flow. If every driver takes the path that looks most favourable to them, the resultant running times need not be minimal. Furthermore, it is indicated by an example that an extension of the road network may cause a redistribution of the traffic that results in longer individual running times."
Adding extra capacity to a network when the moving entities selfishly choose their route can in some cases reduce overall performance. That is because the Nash equilibrium of such a system is not necessarily optimal. The network change induces a new game structure which leads to a (multiplayer) prisoner's dilemma. In a Nash equilibrium, drivers have no incentive to change their routes. While the system is not in a Nash equilibrium, individual drivers are able to improve their respective travel times by changing the routes they take. In the case of Braess's paradox, drivers will continue to switch until they reach Nash equilibrium despite the reduction in overall performance.
If the latency functions are linear, adding an edge can never make total travel time at equilibrium worse by a factor of more than 4/3.[4]
Possible instances of the paradox in action
Prevalence
In 1983, Steinberg and Zangwill provided, under reasonable assumptions, the necessary and sufficient conditions for Braess's paradox to occur in a general transportation network when a new route is added. (Note that their result applies to the addition of any new route, not just to the case of adding a single link.) As a corollary, they obtain that Braess's paradox is about as likely to occur as not occur when a random new route is added.[5]
Traffic
Braess's paradox has a counterpart in case of a reduction of the road network (which may cause a reduction of individual commuting time).[6]
In Seoul, South Korea , traffic around the city sped up when a motorway was removed as part of the Cheonggyecheon restoration project.[7] In Stuttgart, Germany , after investments into the road network in 1969, the traffic situation did not improve until a section of newly built road was closed for traffic again.[8] In 1990 the temporary closing of 42nd Street in Manhattan, New York City , for Earth Day reduced the amount of congestion in the area.[9] In 2008 Youn, Gastner and Jeong demonstrated specific routes in Boston, New York City and London where that might actually occur and pointed out roads that could be closed to reduce predicted travel times.[10] In 2009, New York experimented with closures of Broadway at Times Square and Herald Square, which resulted in improved traffic flow and permanent pedestrian plazas.[11]
In 2012, Paul Lecroart, of the institute of planning and development of the Île-de-France, wrote that "Despite initial fears, the removal of main roads does not cause deterioration of traffic conditions beyond the starting adjustments. The traffic transfer are limited and below expectations".[6] He also notes that some private vehicle trips (and related economic activity) are not transferred to public transport and simply disappear ("evaporate").[6]
The same phenomenon was also observed when road closing was not part of an urban project but the consequence of an accident. In 2012 in Rouen, a bridge was destroyed by fire. Over the next two years, other bridges were used more, but the total number of cars crossing bridges was reduced.[6]
Electricity
In 2012, scientists at the Max Planck Institute for Dynamics and Self-Organization demonstrated, through computational modelling, the potential for the phenomenon to occur in power transmission networks where power generation is decentralized.[12]
In 2012, an international team of researchers from Institut Néel (CNRS, France), INP (France), IEMN (CNRS, France) and UCL (Belgium) published in Physical Review Letters[13] a paper showing that Braess's paradox may occur in mesoscopic electron systems. In particular, they showed that adding a path for electrons in a nanoscopic network paradoxically reduced its conductance. That was shown both by simulations as well as experiments at low temperature using scanning gate microscopy.
Springs
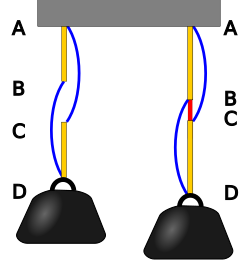
A model with springs and ropes can show that a hung weight can rise in height despite a taut rope in the hanging system being cut, and follows from the same mathematical structure as the original Braess's paradox.[14]
For two identical springs joined in series by a short rope, their total spring constant is half of each individual spring, resulting in a long stretch when a certain weight is hung. This remains the case as we add two longer ropes in slack to connect the lower end of the upper spring to the hung weight (lower end of the lower spring), and the upper end of the lower spring to the hanging point (upper end of the upper spring). However, when the short rope is cut, the longer ropes become taut, and the two springs become parallel (in the mechanical sense) to each other. The total spring constant is twice that of each individual spring, and when the length of the long ropes is not too long, the hung weight will actually be higher compared to before the short rope was cut.
The fact that the hung weight rises despite cutting a taut rope (the short rope) in the hanging system is counter-intuitive, but it does follow from Hooke's law and the way springs work in series and in parallel.
Biology
Adilson E. Motter and collaborators demonstrated that Braess's paradox outcomes may often occur in biological and ecological systems.[15] Motter suggests removing part of a perturbed network could rescue it. For resource management of endangered species food webs, in which extinction of many species might follow sequentially, selective removal of a doomed species from the network could in principle bring about the positive outcome of preventing a series of further extinctions.[16]
Team sports strategy
It has been suggested that in basketball, a team can be seen as a network of possibilities for a route to scoring a basket, with a different efficiency for each pathway, and a star player could reduce the overall efficiency of the team, analogous to a shortcut that is overused increasing the overall times for a journey through a road network. A proposed solution for maximum efficiency in scoring is for a star player to shoot about the same number of shots as teammates. However, this approach is not supported by hard statistical evidence, as noted in the original paper.[17]
Mathematical approach
Example
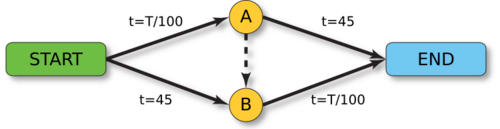
Consider a road network as shown in the adjacent diagram on which 4000 drivers wish to travel from point Start to End. The travel time in minutes on the Start–A road is the number of travellers (T) divided by 100, and on Start–B is a constant 45 minutes (likewise with the roads across from them). If the dashed road does not exist (so the traffic network has 4 roads in total), the time needed to drive Start–A–End route with [math]\displaystyle{ a }[/math] drivers would be [math]\displaystyle{ \tfrac{a}{100} + 45 }[/math]. The time needed to drive the Start–B–End route with [math]\displaystyle{ b }[/math] drivers would be [math]\displaystyle{ \tfrac{b}{100} + 45 }[/math]. As there are 4000 drivers, the fact that [math]\displaystyle{ a + b = 4000 }[/math] can be used to derive the fact that [math]\displaystyle{ a = b = 2000 }[/math] when the system is at equilibrium. Therefore, each route takes [math]\displaystyle{ \tfrac{2000}{100} + 45 = 65 }[/math] minutes. If either route took less time, it would not be a Nash equilibrium: a rational driver would switch from the longer route to the shorter route.
Now suppose the dashed line A–B is a road with an extremely short travel time of approximately 0 minutes. Suppose that the road is opened and one driver tries Start–A–B–End. To his surprise he finds that his time is [math]\displaystyle{ \tfrac{2000}{100} + \tfrac{2001}{100} = 40.01 }[/math] minutes, a saving of almost 25 minutes. Soon, more of the 4000 drivers are trying this new route. The time taken rises from 40.01 and keeps climbing. When the number of drivers trying the new route reaches 2500, with 1500 still in the Start–B–End route, their time will be [math]\displaystyle{ \tfrac{2500}{100} + \tfrac{4000}{100} = 65 }[/math] minutes, which is no improvement over the original route. Meanwhile, those 1500 drivers have been slowed to [math]\displaystyle{ 45 + \tfrac{4000}{100} = 85 }[/math] minutes, a 20-minute increase. They are obliged to switch to the new route via A too, so it now takes [math]\displaystyle{ \tfrac{4000}{100} + \tfrac{4000}{100} = 80 }[/math] minutes. Nobody has any incentive to travel A-End or Start-B because any driver trying them will take 85 minutes. Thus, the opening of the cross route triggers an irreversible change to it by everyone, costing everyone 80 minutes instead of the original 65. If every driver were to agree not to use the A–B path, or if that route were closed, every driver would benefit by a 15-minute reduction in travel time.
Existence of an equilibrium
If one assumes the travel time for each person driving on an edge to be equal, an equilibrium will always exist.
Let [math]\displaystyle{ L_e(x) }[/math] be the formula for the travel time of each person traveling along edge [math]\displaystyle{ e }[/math] when [math]\displaystyle{ x }[/math] people take that edge. Suppose there is a traffic graph with [math]\displaystyle{ x_e }[/math] people driving along edge [math]\displaystyle{ e }[/math]. Let the energy of [math]\displaystyle{ e }[/math], [math]\displaystyle{ E(e) }[/math], be
- [math]\displaystyle{ \sum_{i=1}^{x_e} L_e(i) = L_e(1) + L_e(2) + \cdots + L_e(x_e) }[/math]
(If [math]\displaystyle{ x_e = 0 }[/math] let [math]\displaystyle{ E(e) = 0 }[/math]). Let the total energy of the traffic graph be the sum of the energies of every edge in the graph.
Take a choice of routes that minimizes the total energy. Such a choice must exist because there are finitely many choices of routes. That will be an equilibrium.
Assume, for contradiction, this is not the case. Then, there is at least one driver who can switch the route and improve the travel time. Suppose the original route is [math]\displaystyle{ e_0, e_1, \ldots, e_n }[/math] while the new route is [math]\displaystyle{ e'_0, e'_1, \ldots, e'_m }[/math]. Let [math]\displaystyle{ E }[/math] be total energy of the traffic graph, and consider what happens when the route [math]\displaystyle{ e_0, e_1, ... e_n }[/math] is removed. The energy of each edge [math]\displaystyle{ e_i }[/math] will be reduced by [math]\displaystyle{ L_{e_i}(x_{e_i}) }[/math] and so the [math]\displaystyle{ E }[/math] will be reduced by [math]\displaystyle{ \sum_{i=0}^n L_{e_i}(x_{e_i}) }[/math]. That is simply the total travel time needed to take the original route. If the new route is then added, [math]\displaystyle{ e'_0, e'_1, \ldots, e'_m }[/math], the total energy [math]\displaystyle{ E }[/math] will be increased by the total travel time needed to take the new route. Because the new route is shorter than the original route, [math]\displaystyle{ E }[/math] must decrease relative to the original configuration, contradicting the assumption that the original set of routes minimized the total energy.
Therefore, the choice of routes minimizing total energy is an equilibrium.
Finding an equilibrium
The above proof outlines a procedure known as best response dynamics, which finds an equilibrium for a linear traffic graph and terminates in a finite number of steps. The algorithm is termed "best response" because at each step of the algorithm, if the graph is not at equilibrium then some driver has a best response to the strategies of all other drivers and switches to that response.
Pseudocode for Best Response Dynamics:
Let P be some traffic pattern.
while P is not at equilibrium:
compute the potential energy e of P
for each driver d in P:
for each alternate path p available to d:
compute the potential energy n of the pattern when d takes path p
if n < e:
modify P so that d takes path p
continue the topmost while
At each step, if some particular driver could do better by taking an alternate path (a "best response"), doing so strictly decreases the energy of the graph. If no driver has a best response, the graph is at equilibrium. Since the energy of the graph strictly decreases with each step, the best response dynamics algorithm must eventually halt.
How far from optimal is traffic at equilibrium?
If the travel time functions are linear, that is [math]\displaystyle{ L_e(x) = a_e x + b_e }[/math] for some [math]\displaystyle{ a_e, b_e \geq 0 }[/math], then at worst, traffic in the energy-minimizing equilibrium is twice as bad as socially optimal.[18]
Proof: Let [math]\displaystyle{ Z }[/math] be some traffic configuration, with associated energy [math]\displaystyle{ E(Z) }[/math] and total travel time [math]\displaystyle{ T(Z) }[/math]. For each edge, the energy is the sum of an arithmetic progression, and using the formula for the sum of an arithmetic progression, one can show that [math]\displaystyle{ E(Z)\leq T(Z)\leq 2E(Z) }[/math]. If [math]\displaystyle{ Z_o }[/math] is the socially-optimal traffic flow and [math]\displaystyle{ Z_e }[/math] is the energy-minimizing traffic flow, the inequality implies that [math]\displaystyle{ T(Z_e) \leq 2E(Z_e) \leq 2E(Z_o) \leq 2T(Z_o) }[/math].
Thus, the total travel time for the energy-minimizing equilibrium is at most twice as bad as for the optimal flow.
Dynamics analysis of Braess's paradox
In 2013, Dal Forno and Merlone[19] interpret Braess's paradox as a dynamical ternary choice problem. The analysis shows how the new path changes the problem. Before the new path is available, the dynamics is the same as in binary choices with externalities, but the new path transforms it into a ternary choice problem. The addition of an extra resource enriches the complexity of the dynamics. In fact, there can even be coexistence of cycles, and the implication of the paradox on the dynamics can be seen from both a geometrical and an analytical perspective.
Effect of network topology
Mlichtaich[20] proved that Braess's paradox may occur if and only if the network is not a series-parallel graph.
See also
- Finance:Downs–Thomson paradox – Paradox in traffic engineering related to improvements in the road network
- Physics:Jevons paradox – Efficiency leads to increased demand
- Finance:Marchetti's constant – Average commuting time
- Finance:Lewis–Mogridge position – Theory of road traffic
- Price of anarchy in congestion games - a quantitative analysis of the loss in efficiency caused by congestion externalities.
References
- ↑ Pigou, Arthur Cecil (2017-10-24), "Welfare and Economic Welfare", The Economics of Welfare (Routledge): pp. 3–22, doi:10.4324/9781351304368-1, ISBN 978-1-351-30436-8, http://dx.doi.org/10.4324/9781351304368-1, retrieved 2023-03-24
- ↑ Braess, D. (December 1968). "Über ein Paradoxon aus der Verkehrsplanung". Unternehmensforschung Operations Research - Recherche Opérationnelle 12 (1): 258–268. doi:10.1007/bf01918335. ISSN 0340-9422. http://dx.doi.org/10.1007/bf01918335.
- ↑ New Scientist, 42nd St Paradox: Cull the best to make things better, 16 January 2014 by Justin Mullins
- ↑ Roughgarden, Tim; Tardos, Éva. "How Bad is Selfish Routing?". Journal of the ACM. http://theory.stanford.edu/~tim/papers/routing.pdf.
- ↑ Steinberg, R.; Zangwill, W. I. (1983). "The Prevalence of Braess' Paradox". Transportation Science 17 (3): 301. doi:10.1287/trsc.17.3.301.
- ↑ 6.0 6.1 6.2 6.3 (in French) Olivier Razemon, "Le paradoxde de l'« évaporation » du trafic automobile", Le Monde, Thursday 25 August 2016, page 5. Published on-line as "Quand les voitures s’évaporent" on 24 August 2016 and updated on 25 August 2016 (page visited on 3 August 2023).
- ↑ Easley, D.; Kleinberg, J. (2008). Networks. Cornell Store Press. p. 71.
- ↑ Knödel, W. (31 January 1969). Graphentheoretische Methoden Und Ihre Anwendungen. Springer-Verlag. pp. 57–59. ISBN 978-3-540-04668-4. https://books.google.com/books?id=bJ22pwAACAAJ.
- ↑ Kolata, Gina (1990-12-25). "What if They Closed 42d Street and Nobody Noticed?". New York Times. https://www.nytimes.com/1990/12/25/health/what-if-they-closed-42d-street-and-nobody-noticed.html.
- ↑ Youn, Hyejin; Gastner, Michael; Jeong, Hawoong (2008). "Price of Anarchy in Transportation Networks: Efficiency and Optimality Control". Physical Review Letters 101 (12): 128701. doi:10.1103/PhysRevLett.101.128701. ISSN 0031-9007. PMID 18851419. Bibcode: 2008PhRvL.101l8701Y.
- ↑ Boyd, Andrew. "Braess' Paradox". Engines of Our Ingenuity. Episode 2814.
- ↑ Staff (Max Planck Institute) (September 14, 2012), "Study: Solar and wind energy may stabilize the power grid", R&D Magazine: rdmag.com, https://www.rdworldonline.com/study-solar-and-wind-energy-may-stabilize-the-power-grid/, retrieved September 14, 2012
- ↑ Pala, M. G.; Baltazar, S.; Liu, P.; Sellier, H.; Hackens, B.; Martins, F.; Bayot, V.; Wallart, X. et al. (2012). "Transport Inefficiency in Branched-Out Mesoscopic Networks: An Analog of the Braess Paradox". Physical Review Letters 108 (7): 076802. doi:10.1103/PhysRevLett.108.076802. ISSN 0031-9007. PMID 22401236. Bibcode: 2012PhRvL.108g6802P.
- ↑ Mould, Steve. "The Spring Paradox" (in en). https://www.youtube.com/watch?v=Cg73j3QYRJc.
- ↑ Motter, Adilson E. (2010). "Improved network performance via antagonism: From synthetic rescues to multi-drug combinations". BioEssays 32 (3): 236–245. doi:10.1002/bies.200900128. PMID 20127700.
- ↑ Sahasrabudhe S., Motter A. E., Rescuing ecosystems from extinction cascades through compensatory perturbations, Nature Communications 2, 170 (2011)
- ↑ Skinner, Brian; Gastner, Michael T; Jeong, Hawoong (2009). "The price of anarchy in basketball". Journal of Quantitative Analysis in Sports 6 (1). doi:10.2202/1559-0410.1217. Bibcode: 2009arXiv0908.1801S.
- ↑ Easley, David; Kleinberg, Jon. "Networks, Crowds, and Markets: Reasoning about a Highly Connected World (8.3 Advanced Material: The Social Cost of Traffic at Equilibrium)". Jon Kleinberg. http://www.cs.cornell.edu/home/kleinber/networks-book/networks-book.pdf. – This is the preprint of ISBN:9780521195331
- ↑ Dal Forno, Arianna; Merlone, Ugo (2013). "Border-collision bifurcations in a model of Braess paradox". Mathematics and Computers in Simulation 87: 1–18. doi:10.1016/j.matcom.2012.12.001. ISSN 0378-4754.
- ↑ Milchtaich, Igal (2006-11-01). "Network topology and the efficiency of equilibrium" (in en). Games and Economic Behavior 57 (2): 321–346. doi:10.1016/j.geb.2005.09.005. ISSN 0899-8256. https://www.sciencedirect.com/science/article/pii/S0899825605001284.
Further reading
- Braess, D. (1969). "Über ein Paradoxon aus der Verkehrsplanung" (in de). Unternehmensforschung 12: 258–268. https://homepage.ruhr-uni-bochum.de/Dietrich.Braess/paradox.pdf. (translation by Nagurney & Wakolbinger)
- Katharina Belaga-Werbitzky: „Das Paradoxon von Braess in erweiterten Wheatstone-Netzen mit M/M/1-Bedienern“ ISBN:3-89959-123-2
- Translation of the Braess 1968 article from German to English appears as the article "On a paradox of traffic planning," by D. Braess, A. Nagurney, and T. Wakolbinger in the journal Transportation Science, volume 39, 2005, pp. 446–450. More information
- Irvine, A. D. (1993). "How Braess' paradox solves Newcomb's problem". International Studies in the Philosophy of Science 7 (2): 141–160. doi:10.1080/02698599308573460.
- Steinberg, R.; Zangwill, W. I. (1983). "The Prevalence of Braess' Paradox". Transportation Science 17 (3): 301. doi:10.1287/trsc.17.3.301.
- Rapoport, A.; Kugler, T.; Dugar, S.; Gisches, E. J. (2009). "Choice of routes in congested traffic networks: Experimental tests of the Braess Paradox". Games and Economic Behavior 65 (2): 538–571. doi:10.1016/j.geb.2008.02.007. https://www.parisschoolofeconomics.eu/IMG/pdf/Choices_of_routes.pdf.
- T. Roughgarden. "The Price of Anarchy." MIT Press, Cambridge, MA, 2005.
External links
- Software Testing Paradoxes (December 2005) Direct Link
- Dietrich Braess's homepage
- The Road Network Paradox
- Short video illustrating the Braess Paradox with Lego minifigures
- The Spring Paradox, YouTube video by Steve Mould explaining Braess's Paradox as well as a closely related spring paradox
 |