Philosophy:Prisoner's dilemma

Short description: Standard example in game theory

The prisoner's dilemma is a game theory thought experiment that involves two rational agents, each of whom can cooperate for mutual benefit or betray their partner ("defect") for individual reward. This dilemma was originally framed by Merrill Flood and Melvin Dresher in 1950 while they worked at the RAND Corporation. Albert W. Tucker later formalized the game by structuring the rewards in terms of prison sentences and named it the "prisoner's dilemma".

The prisoner's dilemma models many real-world situations involving strategic behavior. In casual usage, the label "prisoner's dilemma" may be applied to any situation in which two entities could gain important benefits from cooperating or suffer from failing to do so, but find it difficult or expensive to coordinate their activities.

Premise

An example prisoner's dilemma payoff matrix

William Poundstone described this "typical contemporary version" of the game in his 1993 book Prisoner's Dilemma:

Two members of a criminal gang are arrested and imprisoned. Each prisoner is in solitary confinement with no means of speaking to or exchanging messages with the other. The police admit they don't have enough evidence to convict the pair on the principal charge. They plan to sentence both to a year in prison on a lesser charge. Simultaneously, the police offer each prisoner a Faustian bargain. If he testifies against his partner, he will go free while the partner will get three years in prison on the main charge. Oh, yes, there is a catch ... If both prisoners testify against each other, both will be sentenced to two years in jail. The prisoners are given a little time to think this over, but in no case may either learn what the other has decided until he has irrevocably made his decision. Each is informed that the other prisoner is being offered the very same deal. Each prisoner is concerned only with his own welfare—with minimizing his own prison sentence.

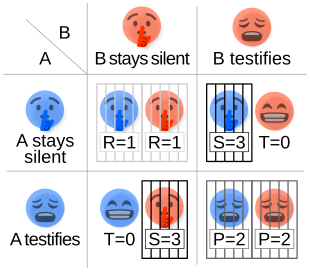
This leads to four different possible outcomes for prisoners A and B:

1. If A and B both remain silent, they will each serve one year in prison.
2. If A testifies against B but B remains silent, A will be set free while B serves three years in prison.
3. If A remains silent but B testifies against A, A will serve three years in prison and B will be set free.
4. If A and B testify against each other, they will each serve two years.

Strategy for the prisoner's dilemma

Two prisoners are separated into individual rooms and cannot communicate with each other. It is assumed that both prisoners understand the nature of the game, have no loyalty to each other, and will have no opportunity for retribution or reward outside of the game. The normal game is shown below:

Prisoner B Prisoner A	Prisoner B stays silent (cooperates)	Prisoner B testifies (defects)
Prisoner A stays silent (cooperates)	Each serves 1 year	Prisoner A: 3 years Prisoner B: goes free
Prisoner A testifies (defects)	Prisoner A: goes free Prisoner B: 3 years	Each serves 2 years

Regardless of what the other decides, each prisoner gets a higher reward by betraying the other ("defecting"). The reasoning involves analyzing both players' best responses: B will either cooperate or defect. If B cooperates, A should defect, because going free is better than serving 1 year. If B defects, A should also defect, because serving 2 years is better than serving 3. So, either way, A should defect since defecting is A's best response regardless of B's strategy. Parallel reasoning will show that B should defect.

Defection always results in a better payoff than cooperation, so it is a strictly dominant strategy for both players. Mutual defection is the only strong Nash equilibrium in the game. Since the collectively ideal result of mutual cooperation is irrational from a self-interested standpoint, this Nash equilibrium is not Pareto efficient.

Generalized form

The structure of the traditional prisoner's dilemma can be generalized from its original prisoner setting. Suppose that the two players are represented by the colors red and blue and that each player chooses to either "cooperate" or "defect".

If both players cooperate, they both receive the reward [math]\displaystyle{ R }[/math] for cooperating. If both players defect, they both receive the punishment payoff [math]\displaystyle{ P }[/math]. If Blue defects while Red cooperates, then Blue receives the temptation payoff [math]\displaystyle{ T }[/math], while Red receives the "sucker's" payoff, [math]\displaystyle{ S }[/math]. Similarly, if Blue cooperates while Red defects, then Blue receives the sucker's payoff [math]\displaystyle{ S }[/math], while Red receives the temptation payoff [math]\displaystyle{ T }[/math].

This can be expressed in normal form:

Canonical prisoner's dilemma payoff matrix

Red Blue	Cooperate	Defect
Cooperate	R R	T S
Defect	S T	P P

and to be a prisoner's dilemma game in the strong sense, the following condition must hold for the payoffs:

[math]\displaystyle{ T \gt R \gt P \gt S }[/math]

The payoff relationship [math]\displaystyle{ R \gt P }[/math] implies that mutual cooperation is superior to mutual defection, while the payoff relationships [math]\displaystyle{ T \gt R }[/math] and [math]\displaystyle{ P \gt S }[/math] imply that defection is the dominant strategy for both agents.

The iterated prisoner's dilemma

If two players play the prisoner's dilemma more than once in succession, remember their opponent's previous actions, and are allowed to change their strategy accordingly, the game is called the iterated prisoner's dilemma.

In addition to the general form above, the iterative version also requires that [math]\displaystyle{ 2R \gt T + S }[/math], to prevent alternating cooperation and defection giving a greater reward than mutual cooperation.

The iterated prisoner's dilemma is fundamental to some theories of human cooperation and trust. Assuming that the game effectively models transactions between two people that require trust, cooperative behavior in populations can be modeled by a multi-player iterated version of the game. In 1975, Grofman and Pool estimated the count of scholarly articles devoted to it at over 2,000. The iterated prisoner's dilemma is also called the "peace-war game".

General strategy

If the iterated prisoner's dilemma is played a finite number of times and both players know this, then the dominant strategy and Nash equilibrium is to defect in all rounds. The proof is inductive: one might as well defect on the last turn, since the opponent will not have a chance to later retaliate. Therefore, both will defect on the last turn. Thus, the player might as well defect on the second-to-last turn, since the opponent will defect on the last no matter what is done, and so on. The same applies if the game length is unknown but has a known upper limit.

For cooperation to emerge between rational players, the number of rounds must be unknown or infinite. In that case, "always defect" may no longer be a strictly dominant strategy but only a Nash equilibrium. As shown by Robert Aumann in a 1959 paper, rational players repeatedly interacting for indefinitely long games can sustain cooperation. Specifically, a player may be less willing to cooperate if their counterpart did not cooperate many times, which causes disappointment. Conversely, as time elapses, the likelihood of cooperation tends to rise, owing to the establishment of a "tacit agreement" among participating players. Another aspect of the iterated prisoner's dilemma is that this tacit agreement between players has always been established successfully even when the number of iterations is made public to both sides.

According to a 2019 experimental study in the American Economic Review that tested what strategies real-life subjects used in iterated prisoner's dilemma situations with perfect monitoring, the majority of chosen strategies were always to defect, tit-for-tat, and grim trigger. Which strategy the subjects chose depended on the parameters of the game.

Axelrod's contest and successful strategy conditions

Interest in the iterated prisoner's dilemma was kindled by Robert Axelrod in his 1984 book The Evolution of Cooperation, in which he reports on a tournament that he organized of the N-step prisoner's dilemma (with N fixed) in which participants have to choose their strategy repeatedly and remember their previous encounters. Axelrod invited academic colleagues from around the world to devise computer strategies to compete in an iterated prisoner's dilemma tournament. The programs that were entered varied widely in algorithmic complexity, initial hostility, capacity for forgiveness, and so forth.

Axelrod discovered that when these encounters were repeated over a long period of time with many players, each with different strategies, greedy strategies tended to do very poorly in the long run while more altruistic strategies did better, as judged purely by self-interest. He used this to show a possible mechanism for the evolution of altruistic behavior from mechanisms that are initially purely selfish, by natural selection.

The winning deterministic strategy was tit for tat, developed and entered into the tournament by Anatol Rapoport. It was the simplest of any program entered, containing only four lines of BASIC, and won the contest. The strategy is simply to cooperate on the first iteration of the game; after that, the player does what his or her opponent did on the previous move. Depending on the situation, a slightly better strategy can be "tit for tat with forgiveness": when the opponent defects, on the next move, the player sometimes cooperates anyway, with a small probability (around 1–5%, depending on the lineup of opponents). This allows for occasional recovery from getting trapped in a cycle of defections.

After analyzing the top-scoring strategies, Axelrod stated several conditions necessary for a strategy to succeed:

• Nice: The strategy will not defect before its opponent does (this is sometimes referred to as an "optimistic" algorithm). Almost all the top-scoring strategies were nice. A purely selfish strategy will not "cheat" on its opponent for purely self-interested reasons first.
• Retaliating: The strategy must sometimes retaliate. An example of a non-retaliating strategy is Always Cooperate, a very bad choice that will frequently be exploited by "nasty" strategies.
• Forgiving: Successful strategies must be forgiving. Though players will retaliate, they will cooperate again if the opponent does not continue to defect. This can stop long runs of revenge and counter-revenge, maximizing points.
• Non-envious: The strategy must not strive to score more than the opponent.

In contrast to the one-time prisoner's dilemma game, the optimal strategy in the iterated prisoner's dilemma depends upon the strategies of likely opponents, and how they will react to defections and cooperation. For example, if a population consists entirely of players who always defect, except for one who follows the tit-for-tat strategy, that person is at a slight disadvantage because of the loss on the first turn. In such a population, the optimal strategy is to defect every time. More generally, given a population with a certain percentage of always-defectors with the rest being tit-for-tat players, the optimal strategy depends on the percentage and number of iterations played.

Other strategies

Deriving the optimal strategy is generally done in two ways:

• Bayesian Nash equilibrium: If the statistical distribution of opposing strategies can be determined an optimal counter-strategy can be derived analytically.
• Monte Carlo simulations of populations have been made, where individuals with low scores die off, and those with high scores reproduce (a genetic algorithm for finding an optimal strategy). The mix of algorithms in the final population generally depends on the mix in the initial population. The introduction of mutation (random variation during reproduction) lessens the dependency on the initial population; empirical experiments with such systems tend to produce tit-for-tat players, but no analytic proof exists that this will always occur.

In the strategy called win-stay, lose-switch, faced with a failure to cooperate, the player switches strategy the next turn. In certain circumstances, Pavlov beats all other strategies by giving preferential treatment to co-players using a similar strategy.

Although tit-for-tat is considered the most robust basic strategy, a team from Southampton University in England introduced a more successful strategy at the 20th-anniversary iterated prisoner's dilemma competition. It relied on collusion between programs to achieve the highest number of points for a single program. The university submitted 60 programs to the competition, which were designed to recognize each other through a series of five to ten moves at the start. Once this recognition was made, one program would always cooperate and the other would always defect, assuring the maximum number of points for the defector. If the program realized that it was playing a non-Southampton player, it would continuously defect in an attempt to minimize the competing program's score. As a result, the 2004 Prisoners' Dilemma Tournament results show University of Southampton's strategies in the first three places (and a number of positions towards the bottom), despite having fewer wins and many more losses than the GRIM strategy. The Southampton strategy takes advantage of the fact that multiple entries were allowed in this particular competition and that a team's performance was measured by that of the highest-scoring player (meaning that the use of self-sacrificing players was a form of minmaxing).

Because of this new rule, this competition also has little theoretical significance when analyzing single-agent strategies as compared to Axelrod's seminal tournament. But it provided a basis for analyzing how to achieve cooperative strategies in multi-agent frameworks, especially in the presence of noise.

Long before this new-rules tournament was played, Dawkins, in his book The Selfish Gene, pointed out the possibility of such strategies winning if multiple entries were allowed, but remarked that Axelrod would most likely not have allowed them if they had been submitted. It also relies on circumventing the rule that no communication is allowed between players, which the Southampton programs arguably did with their preprogrammed "ten-move dance" to recognize one another, reinforcing how valuable communication can be in shifting the balance of the game.

Even without implicit collusion between software strategies, tit-for-tat is not always the absolute winner of any given tournament; more precisely, its long-run results over a series of tournaments outperform its rivals, but this does not mean it is the most successful in the short term. The same applies to tit-for-tat with forgiveness and other optimal strategies.

This can also be illustrated using the Darwinian ESS simulation. In such a simulation, tit-for-tat will almost always come to dominate, though nasty strategies will drift in and out of the population because a tit-for-tat population is penetrable by non-retaliating nice strategies, which in turn are easy prey for the nasty strategies. Dawkins showed that here, no static mix of strategies forms a stable equilibrium, and the system will always oscillate between bounds.

Stochastic iterated prisoner's dilemma

In a stochastic iterated prisoner's dilemma game, strategies are specified in terms of "cooperation probabilities". In an encounter between player X and player Y, X's strategy is specified by a set of probabilities P of cooperating with Y. P is a function of the outcomes of their previous encounters or some subset thereof. If P is a function of only their most recent n encounters, it is called a "memory-n" strategy. A memory-1 strategy is then specified by four cooperation probabilities: [math]\displaystyle{ P=\{P_{cc},P_{cd},P_{dc},P_{dd}\} }[/math], where P_cd is the probability that X will cooperate in the present encounter given that the previous encounter was characterized by X cooperating and Y defecting. If each of the probabilities are either 1 or 0, the strategy is called deterministic. An example of a deterministic strategy is the tit-for-tat strategy written as [math]\displaystyle{ P=\{1,0,1,0\} }[/math], in which X responds as Y did in the previous encounter. Another is the win-stay, lose switch strategy written as [math]\displaystyle{ P=\{1,0,0,1\} }[/math]. It has been shown that for any memory-n strategy there is a corresponding memory-1 strategy that gives the same statistical results, so that only memory-1 strategies need be considered.

If [math]\displaystyle{ P }[/math] is defined as the above 4-element strategy vector of X and [math]\displaystyle{ Q=\{Q_{cc},Q_{cd},Q_{dc},Q_{dd}\} }[/math] as the 4-element strategy vector of Y (where the indices are from Y's point of view), a transition matrix M may be defined for X whose ij-th entry is the probability that the outcome of a particular encounter between X and Y will be j given that the previous encounter was i, where i and j are one of the four outcome indices: cc, cd, dc, or dd. For example, from X's point of view, the probability that the outcome of the present encounter is cd given that the previous encounter was cd is equal to [math]\displaystyle{ M_{cd,cd}=P_{cd}(1-Q_{dc}) }[/math]. Under these definitions, the iterated prisoner's dilemma qualifies as a stochastic process and M is a stochastic matrix, allowing all of the theory of stochastic processes to be applied.

One result of stochastic theory is that there exists a stationary vector v for the matrix v such that [math]\displaystyle{ v\cdot M=v }[/math]. Without loss of generality, it may be specified that v is normalized so that the sum of its four components is unity. The ij-th entry in [math]\displaystyle{ M^n }[/math] will give the probability that the outcome of an encounter between X and Y will be j given that the encounter n steps previous is i. In the limit as n approaches infinity, M will converge to a matrix with fixed values, giving the long-term probabilities of an encounter producing j independent of i. In other words, the rows of [math]\displaystyle{ M^\infty }[/math] will be identical, giving the long-term equilibrium result probabilities of the iterated prisoner's dilemma without the need to explicitly evaluate a large number of interactions. It can be seen that v is a stationary vector for [math]\displaystyle{ M^n }[/math] and particularly [math]\displaystyle{ M^\infty }[/math], so that each row of [math]\displaystyle{ M^\infty }[/math] will be equal to v. Thus, the stationary vector specifies the equilibrium outcome probabilities for X. Defining [math]\displaystyle{ S_x=\{R,S,T,P\} }[/math] and [math]\displaystyle{ S_y=\{R,T,S,P\} }[/math] as the short-term payoff vectors for the {cc,cd,dc,dd} outcomes (from X's point of view), the equilibrium payoffs for X and Y can now be specified as [math]\displaystyle{ s_x=v\cdot S_x }[/math] and [math]\displaystyle{ s_y=v\cdot S_y }[/math], allowing the two strategies P and Q to be compared for their long-term payoffs.

Zero-determinant strategies

The relationship between zero-determinant (ZD), cooperating and defecting strategies in the iterated prisoner's dilemma (iterated prisoner's dilemma)

In 2012, William H. Press and Freeman Dyson published a new class of strategies for the stochastic iterated prisoner's dilemma called "zero-determinant" (ZD) strategies. The long term payoffs for encounters between X and Y can be expressed as the determinant of a matrix which is a function of the two strategies and the short term payoff vectors: [math]\displaystyle{ s_x = D(P, Q, S_x) }[/math] and [math]\displaystyle{ s_y = D(P, Q, S_y) }[/math], which do not involve the stationary vector v. Since the determinant function [math]\displaystyle{ s_y = D(P, Q, f) }[/math] is linear in [math]\displaystyle{ f }[/math], it follows that [math]\displaystyle{ \alpha s_x + \beta s_y + \gamma = D(P, Q, \alpha S_x + \beta S_y + \gamma U) }[/math] (where [math]\displaystyle{ U =\{1,1,1,1 \} }[/math]). Any strategies for which [math]\displaystyle{ D(P, Q, \alpha S_x + \beta S_y + \gamma U) = 0 }[/math] are by definition a ZD strategy, and the long-term payoffs obey the relation [math]\displaystyle{ \alpha s_x + \beta s_y + \gamma = 0 }[/math].

Tit-for-tat is a ZD strategy which is "fair", in the sense of not gaining advantage over the other player. But the ZD space also contains strategies that, in the case of two players, can allow one player to unilaterally set the other player's score or alternatively force an evolutionary player to achieve a payoff some percentage lower than his own. The extorted player could defect, but would thereby hurt himself by getting a lower payoff. Thus, extortion solutions turn the iterated prisoner's dilemma into a sort of ultimatum game. Specifically, X is able to choose a strategy for which [math]\displaystyle{ D(P, Q, \beta S_y + \gamma U) = 0 }[/math], unilaterally setting s_y to a specific value within a particular range of values, independent of Y's strategy, offering an opportunity for X to "extort" player Y (and vice versa). But if X tries to set s_x to a particular value, the range of possibilities is much smaller, consisting only of complete cooperation or complete defection.

An extension of the iterated prisoner's dilemma is an evolutionary stochastic iterated prisoner's dilemma, in which the relative abundance of particular strategies is allowed to change, with more successful strategies relatively increasing. This process may be accomplished by having less successful players imitate the more successful strategies, or by eliminating less successful players from the game, while multiplying the more successful ones. It has been shown that unfair ZD strategies are not evolutionarily stable. The key intuition is that an evolutionarily stable strategy must not only be able to invade another population (which extortionary ZD strategies can do) but must also perform well against other players of the same type (which extortionary ZD players do poorly because they reduce each other's surplus).

Theory and simulations confirm that beyond a critical population size, ZD extortion loses out in evolutionary competition against more cooperative strategies, and as a result, the average payoff in the population increases when the population is larger. In addition, there are some cases in which extortioners may even catalyze cooperation by helping to break out of a face-off between uniform defectors and win–stay, lose–switch agents.

While extortionary ZD strategies are not stable in large populations, another ZD class called "generous" strategies is both stable and robust. When the population is not too small, these strategies can supplant any other ZD strategy and even perform well against a broad array of generic strategies for iterated prisoner's dilemma, including win–stay, lose–switch. This was proven specifically for the donation game by Alexander Stewart and Joshua Plotkin in 2013. Generous strategies will cooperate with other cooperative players, and in the face of defection, the generous player loses more utility than its rival. Generous strategies are the intersection of ZD strategies and so-called "good" strategies, which were defined by Ethan Akin to be those for which the player responds to past mutual cooperation with future cooperation and splits expected payoffs equally if he receives at least the cooperative expected payoff. Among good strategies, the generous (ZD) subset performs well when the population is not too small. If the population is very small, defection strategies tend to dominate.

Continuous iterated prisoner's dilemma

Most work on the iterated prisoner's dilemma has focused on the discrete case, in which players either cooperate or defect, because this model is relatively simple to analyze. However, some researchers have looked at models of the continuous iterated prisoner's dilemma, in which players are able to make a variable contribution to the other player. Le and Boyd found that in such situations, cooperation is much harder to evolve than in the discrete iterated prisoner's dilemma. In a continuous prisoner's dilemma, if a population starts off in a non-cooperative equilibrium, players who are only marginally more cooperative than non-cooperators get little benefit from assorting with one another. By contrast, in a discrete prisoner's dilemma, tit-for-tat cooperators get a big payoff boost from assorting with one another in a non-cooperative equilibrium, relative to non-cooperators. Since nature arguably offers more opportunities for variable cooperation rather than a strict dichotomy of cooperation or defection, the continuous prisoner's dilemma may help explain why real-life examples of tit-for-tat-like cooperation are extremely rare even though tit-for-tat seems robust in theoretical models.

Real-life examples

Many instances of human interaction and natural processes have payoff matrices like the prisoner's dilemma's. It is therefore of interest to the social sciences, such as economics, politics, and sociology, as well as to the biological sciences, such as ethology and evolutionary biology. Many natural processes have been abstracted into models in which living beings are engaged in endless games of prisoner's dilemma.

Environmental studies

In environmental studies, the dilemma is evident in crises such as global climate change. It is argued all countries will benefit from a stable climate, but any single country is often hesitant to curb CO
2 emissions. The immediate benefit to any one country from maintaining current behavior is perceived to be greater than the purported eventual benefit to that country if all countries' behavior was changed, therefore explaining the impasse concerning climate-change in 2007.

An important difference between climate-change politics and the prisoner's dilemma is uncertainty; the extent and pace at which pollution can change climate is not known. The dilemma faced by governments is therefore different from the prisoner's dilemma in that the payoffs of cooperation are unknown. This difference suggests that states will cooperate much less than in a real iterated prisoner's dilemma, so that the probability of avoiding a possible climate catastrophe is much smaller than that suggested by a game-theoretical analysis of the situation using a real iterated prisoner's dilemma.

Thomas Osang and Arundhati Nandy provide a theoretical explanation with proofs for a regulation-driven win-win situation along the lines of Michael Porter's hypothesis, in which government regulation of competing firms is substantial.

Animals

Cooperative behavior of many animals can be understood as an example of the iterated prisoner's dilemma. Often animals engage in long-term partnerships; for example, guppies inspect predators cooperatively in groups, and they are thought to punish non-cooperative inspectors.

Vampire bats are social animals that engage in reciprocal food exchange. Applying the payoffs from the prisoner's dilemma can help explain this behavior.

Psychology

In addiction research and behavioral economics, George Ainslie points out that addiction can be cast as an intertemporal prisoner's dilemma problem between the present and future selves of the addict. In this case, "defecting" means relapsing, where not relapsing both today and in the future is by far the best outcome. The case where one abstains today but relapses in the future is the worst outcome: in some sense, the discipline and self-sacrifice involved in abstaining today have been "wasted" because the future relapse means that the addict is right back where they started and will have to start over. Relapsing today and tomorrow is a slightly "better" outcome, because while the addict is still addicted, they haven't put the effort in to trying to stop. The final case, where one engages in the addictive behavior today while abstaining tomorrow, has the problem that (as in other prisoner's dilemmas) there is an obvious benefit to defecting "today", but tomorrow one will face the same prisoner's dilemma, and the same obvious benefit will be present then, ultimately leading to an endless string of defections.

In The Science of Trust, John Gottman defines good relationships as those where partners know not to enter into mutual defection behavior, or at least not to get dynamically stuck there in a loop. In cognitive neuroscience, fast brain signaling associated with processing different rounds may indicate choices at the next round. Mutual cooperation outcomes entail brain activity changes predictive of how quickly a person will cooperate in kind at the next opportunity; this activity may be linked to basic homeostatic and motivational processes, possibly increasing the likelihood of short-cutting into mutual cooperation.

Economics

The prisoner's dilemma has been called the E. coli of social psychology, and it has been used widely to research various topics such as oligopolistic competition and collective action to produce a collective good.

Advertising is sometimes cited as a real example of the prisoner's dilemma. When cigarette advertising was legal in the United States, competing cigarette manufacturers had to decide how much money to spend on advertising. The effectiveness of Firm A's advertising was partially determined by the advertising conducted by Firm B. Likewise, the profit derived from advertising for Firm B is affected by the advertising conducted by Firm A. If both Firm A and Firm B chose to advertise during a given period, then the advertisement from each firm negates the other's, receipts remain constant, and expenses increase due to the cost of advertising. Both firms would benefit from a reduction in advertising. However, should Firm B choose not to advertise, Firm A could benefit greatly by advertising. Nevertheless, the optimal amount of advertising by one firm depends on how much advertising the other undertakes. As the best strategy is dependent on what the other firm chooses there is no dominant strategy, which makes it slightly different from a prisoner's dilemma. The outcome is similar, though, in that both firms would be better off were they to advertise less than in the equilibrium.

Sometimes cooperative behaviors do emerge in business situations. For instance, cigarette manufacturers endorsed the making of laws banning cigarette advertising, understanding that this would reduce costs and increase profits across the industry.

Without enforceable agreements, members of a cartel are also involved in a (multi-player) prisoner's dilemma. "Cooperating" typically means agreeing to a price floor, while "defecting" means selling under this minimum level, instantly taking business from other cartel members. Anti-trust authorities want potential cartel members to mutually defect, ensuring the lowest possible prices for consumers.

Sport

Doping in sport has been cited as an example of a prisoner's dilemma. Two competing athletes have the option to use an illegal and/or dangerous drug to boost their performance. If neither athlete takes the drug, then neither gains an advantage. If only one does, then that athlete gains a significant advantage over the competitor, reduced by the legal and/or medical dangers of having taken the drug. But if both athletes take the drug, the benefits cancel out and only the dangers remain, putting them both in a worse position than if neither had doped.

International politics

In international relations theory, the prisoner's dilemma is often used to demonstrate why cooperation fails in situations when cooperation between states is collectively optimal but individually suboptimal. A classic example is the security dilemma, whereby an increase in one state's security (such as increasing its military strength) leads other states to fear for their own security out of fear of offensive action. Consequently, security-increasing measures can lead to tensions, escalation or conflict with one or more other parties, producing an outcome which no party truly desires. The security dilemma is particularly intense in situations when it is hard to distinguish offensive weapons from defensive weapons, and offense has the advantage in any conflict over defense.

The prisoner's dilemma has frequently been used by realist international relations theorists to demonstrate the why all states (regardless of their internal policies or professed ideology) under international anarchy will struggle to cooperate with one another even when all benefit from such cooperation.

Critics of realism argue that iteration and extending the shadow of the future are solutions to the prisoner's dilemma. When actors play the prisoner's dilemma once, they have incentives to defect, but when they expect to play it repeatedly, they have greater incentives to cooperate.

Multiplayer dilemmas

Many real-life dilemmas involve multiple players. Although metaphorical, Hardin's tragedy of the commons may be viewed as an example of a multi-player generalization of the prisoner's dilemma: each villager makes a choice for personal gain or restraint. The collective reward for unanimous or frequent defection is very low payoffs and the destruction of the commons.

The commons are not always exploited: William Poundstone, in a book about the prisoner's dilemma, describes a situation in New Zealand where newspaper boxes are left unlocked. It is possible for people to take a paper without paying (defecting), but very few do, feeling that if they do not pay then neither will others, destroying the system. Subsequent research by Elinor Ostrom, winner of the 2009 Nobel Memorial Prize in Economic Sciences, hypothesized that the tragedy of the commons is oversimplified, with the negative outcome influenced by outside influences. Without complicating pressures, groups communicate and manage the commons among themselves for their mutual benefit, enforcing social norms to preserve the resource and achieve the maximum good for the group, an example of effecting the best-case outcome for prisoner's dilemma.

Related games

Closed-bag exchange

The prisoner's dilemma as a briefcase exchange

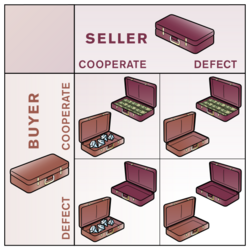
Douglas Hofstadter suggested that people often find problems such as the prisoner's dilemma problem easier to understand when it is illustrated in the form of a simple game, or trade-off. One of several examples he used was "closed bag exchange":

Two people meet and exchange closed bags, with the understanding that one of them contains money, and the other contains a purchase. Either player can choose to honor the deal by putting into his or her bag what he or she agreed, or he or she can defect by handing over an empty bag.

Friend or Foe?

Friend or Foe? is a game show that aired from 2002 to 2003 on the Game Show Network in the US. On the game show, three pairs of people compete. When a pair is eliminated, they play a game similar to the prisoner's dilemma to determine how the winnings are split. If they both cooperate (Friend), they share the winnings 50–50. If one cooperates and the other defects (Foe), the defector gets all the winnings, and the cooperator gets nothing. If both defect, both leave with nothing. Notice that the reward matrix is slightly different from the standard one given above, as the rewards for the "both defect" and the "cooperate while the opponent defects" cases are identical. This makes the "both defect" case a weak equilibrium, compared with being a strict equilibrium in the standard prisoner's dilemma. If a contestant knows that their opponent is going to vote "Foe", then their own choice does not affect their own winnings. In a specific sense, Friend or Foe has a rewards model between prisoner's dilemma and the game of Chicken.

The rewards matrix is

Pair 2 Pair 1	"Friend" (cooperate)	"Foe" (defect)
"Friend" (cooperate)	1 1	2 0
"Foe" (defect)	0 2	0 0

This payoff matrix has also been used on the United Kingdom television programs Trust Me, Shafted, The Bank Job and Golden Balls, and on the United States game shows Take It All, as well as for the winning couple on the reality shows Bachelor Pad and Love Island. Game data from the Golden Balls series has been analyzed by a team of economists, who found that cooperation was "surprisingly high" for amounts of money that would seem consequential in the real world but were comparatively low in the context of the game.

Iterated snowdrift

Researchers from the University of Lausanne and the University of Edinburgh have suggested that the "Iterated Snowdrift Game" may more closely reflect real-world social situations, although this model is actually a chicken game. In this model, the risk of being exploited through defection is lower, and individuals always gain from taking the cooperative choice. The snowdrift game imagines two drivers who are stuck on opposite sides of a snowdrift, each of whom is given the option of shoveling snow to clear a path or remaining in their car. A player's highest payoff comes from leaving the opponent to clear all the snow by themselves, but the opponent is still nominally rewarded for their work.

This may better reflect real-world scenarios, the researchers giving the example of two scientists collaborating on a report, both of whom would benefit if the other worked harder. "But when your collaborator doesn't do any work, it's probably better for you to do all the work yourself. You'll still end up with a completed project."

Example snowdrift payouts (A, B) B   A Cooperates Defects Cooperates 500, 500 200, 800 Defects 800, 200 0, 0

Example prisoner's dilemma payouts (A, B) B   A Cooperates Defects Cooperates 500, 500 −200, 1200 Defects 1200, −200 0, 0

Coordination games

In coordination games, players must coordinate their strategies for a good outcome. An example is two cars that abruptly meet in a blizzard; each must choose whether to swerve left or right. If both swerve left, or both right, the cars do not collide. The local left- and right-hand traffic convention helps to co-ordinate their actions.

Symmetrical co-ordination games include Stag hunt and Bach or Stravinsky.

Asymmetric prisoner's dilemmas

A more general set of games is asymmetric. As in the prisoner's dilemma, the best outcome is cooperation, and there are motives for defection. Unlike the symmetric prisoner's dilemma, though, one player has more to lose and/or more to gain than the other. Some such games have been described as a prisoner's dilemma in which one prisoner has an alibi, hence the term "alibi game".

In experiments, players getting unequal payoffs in repeated games may seek to maximize profits, but only under the condition that both players receive equal payoffs; this may lead to a stable equilibrium strategy in which the disadvantaged player defects every X game, while the other always co-operates. Such behavior may depend on the experiment's social norms around fairness.

Software

Several software packages have been created to run simulations and tournaments of the prisoner's dilemma, some of which have their source code available:

• The source code for the second tournament run by Robert Axelrod (written by Axelrod and many contributors in Fortran) is available online
• Prison, a library written in Java, last updated in 1998
• Axelrod-Python, written in Python
• Evoplex, a fast agent-based modeling program released in 2018 by Marcos Cardinot

In fiction

Hannu Rajaniemi set the opening scene of his The Quantum Thief trilogy in a "dilemma prison". The main theme of the series has been described as the "inadequacy of a binary universe" and the ultimate antagonist is a character called the All-Defector. The first book in the series was published in 2010, with the two sequels, The Fractal Prince and The Causal Angel, published in 2012 and 2014, respectively.

A game modeled after the iterated prisoner's dilemma is a central focus of the 2012 video game Zero Escape and a minor part in its 2016 sequel Zero Escape: Zero Time Dilemma.

In The Mysterious Benedict Society and the Prisoner's Dilemma by Trenton Lee Stewart, the main characters start by playing a version of the game and escaping from the "prison" altogether. Later, they become actual prisoners and escape once again.

In The Adventure Zone: Balance during The Suffering Game subarc, the player characters are twice presented with the prisoner's dilemma during their time in two liches' domain, once cooperating and once defecting.

In the 8th novel from the author James S. A. Corey Tiamat's Wrath, Winston Duarte explains the prisoner's dilemma to his 14-year-old daughter, Teresa, to train her in strategic thinking.

The 2008 film The Dark Knight includes a scene loosely based on the problem in which the Joker rigs two ferries, one containing prisoners and the other containing civilians, arming both groups with the means to detonate the bomb on each other's ferries, threatening to detonate them both if they hesitate.

See also

• Abilene paradox
• Centipede game
• Christmas truce
• Externality
• Folk theorem (game theory)
• Free-rider problem
• Gift-exchange game
• Hobbesian trap
• Innocent prisoner's dilemma
• Liar Game
• Metagame
• Optional prisoner's dilemma
• Prisoner's dilemma and cooperation
• Public goods game
• Reciprocal altruism
• Rent-seeking
• Social preferences
• Superrationality
• Swift trust theory
• Tragedy of the commons
• Traveler's dilemma
• Unscrupulous diner's dilemma

References

Bibliography

• Poundstone, William (1993). Prisoner's Dilemma (1st Anchor Books ed.). New York: Anchor. ISBN 0-385-41580-X. https://archive.org/details/prisonersdilemma00poun. 

Further reading

• Amadae, S. (2016). "Prisoner's Dilemma", Prisoners of Reason. Cambridge University Press , NY, pp. 24–61.
• Aumann, Robert (1959). "Acceptable points in general cooperative n-person games". in Luce, R. D.; Tucker, A. W.. Contributions to the Theory 23 of Games IV. Annals of Mathematics Study. 40. Princeton NJ: Princeton University Press. pp. 287–324. 
• Axelrod, R. (1984). The Evolution of Cooperation. ISBN 0-465-02121-2
• Bicchieri, Cristina (1993). Rationality and Coordination. Cambridge University Press .
• Chess, David M. (December 1988). "Simulating the evolution of behavior: the iterated prisoners' dilemma problem". Complex Systems 2 (6): 663–70. http://www.complex-systems.com/pdf/02-6-4.pdf. 
• Collins, Rory W. (March 2022). "The prisoner's dilemma paradox: Rationality, morality, and reciprocity". Think: Philosophy for Everyone 21 (61): 45–55. doi:10.1017/S1477175621000464. 
• Dresher, M. (1961). The Mathematics of Games of Strategy: Theory and Applications Prentice-Hall, Englewood Cliffs, NJ.
• Greif, A. (2006). Institutions and the Path to the Modern Economy: Lessons from Medieval Trade. Cambridge University Press, Cambridge, UK.
• Kopelman, Shirli (February 2020). "Tit for tat and beyond: the legendary work of Anatol Rapoport". Negotiation and Conflict Management Research 13 (1): 60–84. doi:10.1111/ncmr.12172. 
• Rapoport, Anatol and Albert M. Chammah (1965). Prisoner's Dilemma. University of Michigan Press.
• Schneider, Mark; Shields, Timothy W. (June 2022). "Motives for cooperation in the one-shot prisoner's dilemma". Journal of Behavioral Finance 23 (4): 438–456. doi:10.1080/15427560.2022.2081974. https://digitalcommons.chapman.edu/cgi/viewcontent.cgi?article=1368&context=esi_working_papers. 

External links

• Prisoner's Dilemma (Stanford Encyclopedia of Philosophy)
• The Bowerbird's Dilemma The Prisoner's Dilemma in ornithology – mathematical cartoon by Larry Gonick.
• The Prisoner's Dilemma The Prisoner's Dilemma with Lego minifigures.
• Dixit, Avinash; Nalebuff, Barry (2008). "Prisoner's Dilemma". in David R. Henderson. Concise Encyclopedia of Economics (2nd ed.). Indianapolis: Library of Economics and Liberty. ISBN 978-0865976658. OCLC 237794267. http://www.econlib.org/library/Enc/PrisonersDilemma.html. 
• Game Theory 101: Prisoner's Dilemma
• Dawkins: Nice Guys Finish First
• Axelrod Iterated Prisoner's Dilemma Python library
• Play Prisoner's Dilemma on oTree (N/A 11-5-17)
• Nicky Case's Evolution of Trust, an example of the donation game
• Iterated Prisoner's Dilemma online game by Wayne Davis
• What The Prisoner's Dilemma Reveals About Life, The Universe, and Everything by Veritasium