Cauchy index

In mathematical analysis, the Cauchy index is an integer associated to a real rational function over an interval. By the Routh–Hurwitz theorem, we have the following interpretation: the Cauchy index of

r(x) = p(x)/q(x)

over the real line is the difference between the number of roots of f(z) located in the right half-plane and those located in the left half-plane. The complex polynomial f(z) is such that

f(iy) = q(y) + ip(y).

We must also assume that p has degree less than the degree of q.

Definition

• The Cauchy index was first defined for a pole s of the rational function r by Augustin-Louis Cauchy in 1837 using one-sided limits as:

[math]\displaystyle{ I_sr = \begin{cases} +1, & \text{if } \displaystyle\lim_{x\uparrow s}r(x)=-\infty \;\land\; \lim_{x\downarrow s}r(x)=+\infty, \\ -1, & \text{if } \displaystyle\lim_{x\uparrow s}r(x)=+\infty \;\land\; \lim_{x\downarrow s}r(x)=-\infty, \\ 0, & \text{otherwise.} \end{cases} }[/math]

• A generalization over the compact interval [a,b] is direct (when neither a nor b are poles of r(x)): it is the sum of the Cauchy indices [math]\displaystyle{ I_s }[/math] of r for each s located in the interval. We usually denote it by [math]\displaystyle{ I_a^br }[/math].
• We can then generalize to intervals of type [math]\displaystyle{ [-\infty,+\infty] }[/math] since the number of poles of r is a finite number (by taking the limit of the Cauchy index over [a,b] for a and b going to infinity).

Examples

A rational function

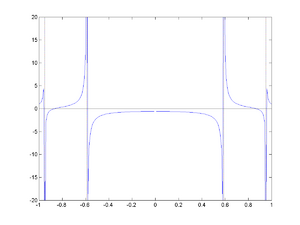
• Consider the rational function:

[math]\displaystyle{ r(x)=\frac{4x^3 -3x}{16x^5 -20x^3 +5x}=\frac{p(x)}{q(x)}. }[/math]

We recognize in p(x) and q(x) respectively the Chebyshev polynomials of degree 3 and 5. Therefore, r(x) has poles [math]\displaystyle{ x_1=0.9511 }[/math], [math]\displaystyle{ x_2=0.5878 }[/math], [math]\displaystyle{ x_3=0 }[/math], [math]\displaystyle{ x_4=-0.5878 }[/math] and [math]\displaystyle{ x_5=-0.9511 }[/math], i.e. [math]\displaystyle{ x_j=\cos((2i-1)\pi/2n) }[/math] for [math]\displaystyle{ j = 1,...,5 }[/math]. We can see on the picture that [math]\displaystyle{ I_{x_1}r=I_{x_2}r=1 }[/math] and [math]\displaystyle{ I_{x_4}r=I_{x_5}r=-1 }[/math]. For the pole in zero, we have [math]\displaystyle{ I_{x_3}r=0 }[/math] since the left and right limits are equal (which is because p(x) also has a root in zero). We conclude that [math]\displaystyle{ I_{-1}^1r=0=I_{-\infty}^{+\infty}r }[/math] since q(x) has only five roots, all in [−1,1]. We cannot use here the Routh–Hurwitz theorem as each complex polynomial with f(iy) = q(y) + ip(y) has a zero on the imaginary line (namely at the origin).

External links

• The Cauchy Index