One-sided limit
In calculus, a one-sided limit refers to either one of the two limits of a function [math]\displaystyle{ f(x) }[/math] of a real variable [math]\displaystyle{ x }[/math] as [math]\displaystyle{ x }[/math] approaches a specified point either from the left or from the right.[1][2]
The limit as [math]\displaystyle{ x }[/math] decreases in value approaching [math]\displaystyle{ a }[/math] ([math]\displaystyle{ x }[/math] approaches [math]\displaystyle{ a }[/math] "from the right"[3] or "from above") can be denoted:[1][2]
[math]\displaystyle{ \lim_{x \to a^+}f(x) \quad \text{ or } \quad \lim_{x\,\downarrow\,a}\,f(x) \quad \text{ or } \quad \lim_{x \searrow a}\,f(x) \quad \text{ or } \quad f(x+) }[/math]
The limit as [math]\displaystyle{ x }[/math] increases in value approaching [math]\displaystyle{ a }[/math] ([math]\displaystyle{ x }[/math] approaches [math]\displaystyle{ a }[/math] "from the left"[4][5] or "from below") can be denoted:[1][2]
[math]\displaystyle{ \lim_{x \to a^-}f(x) \quad \text{ or } \quad \lim_{x\,\uparrow\,a}\, f(x) \quad \text{ or } \quad \lim_{x \nearrow a}\,f(x) \quad \text{ or } \quad f(x-) }[/math]
If the limit of [math]\displaystyle{ f(x) }[/math] as [math]\displaystyle{ x }[/math] approaches [math]\displaystyle{ a }[/math] exists then the limits from the left and from the right both exist and are equal. In some cases in which the limit [math]\displaystyle{ \lim_{x \to a} f(x) }[/math] does not exist, the two one-sided limits nonetheless exist. Consequently, the limit as [math]\displaystyle{ x }[/math] approaches [math]\displaystyle{ a }[/math] is sometimes called a "two-sided limit".[citation needed]
It is possible for exactly one of the two one-sided limits to exist (while the other does not exist). It is also possible for neither of the two one-sided limits to exist.
Formal definition
Definition
If [math]\displaystyle{ I }[/math] represents some interval that is contained in the domain of [math]\displaystyle{ f }[/math] and if [math]\displaystyle{ a }[/math] is a point in [math]\displaystyle{ I }[/math] then the right-sided limit as [math]\displaystyle{ x }[/math] approaches [math]\displaystyle{ a }[/math] can be rigorously defined as the value [math]\displaystyle{ R }[/math] that satisfies:[6][verification needed] [math]\displaystyle{ \text{for all } \varepsilon \gt 0\;\text{ there exists some } \delta \gt 0 \;\text{ such that for all } x \in I, \text{ if } \;0 \lt x - a \lt \delta \text{ then } |f(x) - R| \lt \varepsilon, }[/math] and the left-sided limit as [math]\displaystyle{ x }[/math] approaches [math]\displaystyle{ a }[/math] can be rigorously defined as the value [math]\displaystyle{ L }[/math] that satisfies: [math]\displaystyle{ \text{for all } \varepsilon \gt 0\;\text{ there exists some } \delta \gt 0 \;\text{ such that for all } x \in I, \text{ if } \;0 \lt a - x \lt \delta \text{ then } |f(x) - L| \lt \varepsilon. }[/math]
We can represent the same thing more symbolically, as follows.
Let [math]\displaystyle{ I }[/math] represent an interval, where [math]\displaystyle{ I \subseteq \mathrm{domain}(f) }[/math], and [math]\displaystyle{ a \in I }[/math].
- [math]\displaystyle{ \lim_{x \to a^{+}} f(x) = R ~~~ \iff ~~~ (\forall \varepsilon \in \mathbb{R}_{+}, \exists \delta \in \mathbb{R}_{+}, \forall x \in I, (0 \lt x - a \lt \delta \longrightarrow | f(x) - R | \lt \varepsilon)) }[/math]
- [math]\displaystyle{ \lim_{x \to a^{-}} f(x) = L ~~~ \iff ~~~ (\forall \varepsilon \in \mathbb{R}_{+}, \exists \delta \in \mathbb{R}_{+}, \forall x \in I, (0 \lt a - x \lt \delta \longrightarrow | f(x) - L | \lt \varepsilon)) }[/math]
Intuition
In comparison to the formal definition for the limit of a function at a point, the one-sided limit (as the name would suggest) only deals with input values to one side of the approached input value.
For reference, the formal definition for the limit of a function at a point is as follows:
- [math]\displaystyle{ \lim_{x \to a} f(x) = L ~~~ \iff ~~~ \forall \varepsilon \in \mathbb{R}_{+}, \exists \delta \in \mathbb{R}_{+}, \forall x \in I, 0 \lt |x - a| \lt \delta \implies | f(x) - L | \lt \varepsilon }[/math]
To define a one-sided limit, we must modify this inequality. Note that the absolute distance between [math]\displaystyle{ x }[/math] and [math]\displaystyle{ a }[/math] is [math]\displaystyle{ |x - a| = |(-1)(-x + a)| = |(-1)(a - x)| = |(-1)||a - x| = |a - x| }[/math].
For the limit from the right, we want [math]\displaystyle{ x }[/math] to be to the right of [math]\displaystyle{ a }[/math], which means that [math]\displaystyle{ a \lt x }[/math], so [math]\displaystyle{ x - a }[/math] is positive. From above, [math]\displaystyle{ x - a }[/math] is the distance between [math]\displaystyle{ x }[/math] and [math]\displaystyle{ a }[/math]. We want to bound this distance by our value of [math]\displaystyle{ \delta }[/math], giving the inequality [math]\displaystyle{ x - a \lt \delta }[/math]. Putting together the inequalities [math]\displaystyle{ 0 \lt x - a }[/math] and [math]\displaystyle{ x - a \lt \delta }[/math] and using the transitivity property of inequalities, we have the compound inequality [math]\displaystyle{ 0 \lt x - a \lt \delta }[/math].
Similarly, for the limit from the left, we want [math]\displaystyle{ x }[/math] to be to the left of [math]\displaystyle{ a }[/math], which means that [math]\displaystyle{ x \lt a }[/math]. In this case, it is [math]\displaystyle{ a - x }[/math] that is positive and represents the distance between [math]\displaystyle{ x }[/math] and [math]\displaystyle{ a }[/math]. Again, we want to bound this distance by our value of [math]\displaystyle{ \delta }[/math], leading to the compound inequality [math]\displaystyle{ 0 \lt a - x \lt \delta }[/math].
Now, when our value of [math]\displaystyle{ x }[/math] is in its desired interval, we expect that the value of [math]\displaystyle{ f(x) }[/math] is also within its desired interval. The distance between [math]\displaystyle{ f(x) }[/math] and [math]\displaystyle{ L }[/math], the limiting value of the left sided limit, is [math]\displaystyle{ |f(x) - L| }[/math]. Similarly, the distance between [math]\displaystyle{ f(x) }[/math] and [math]\displaystyle{ R }[/math], the limiting value of the right sided limit, is [math]\displaystyle{ |f(x) - R| }[/math]. In both cases, we want to bound this distance by [math]\displaystyle{ \varepsilon }[/math], so we get the following: [math]\displaystyle{ |f(x) - L| \lt \varepsilon }[/math] for the left sided limit, and [math]\displaystyle{ |f(x) - R| \lt \varepsilon }[/math] for the right sided limit.
Examples
Example 1: The limits from the left and from the right of [math]\displaystyle{ g(x) := - \frac{1}{x} }[/math] as [math]\displaystyle{ x }[/math] approaches [math]\displaystyle{ a := 0 }[/math] are [math]\displaystyle{ \lim_{x \to 0^-} {-1/x} = + \infty \qquad \text{ and } \qquad \lim_{x \to 0^+} {-1/x} = - \infty }[/math] The reason why [math]\displaystyle{ \lim_{x \to 0^-} {-1/x} = + \infty }[/math] is because [math]\displaystyle{ x }[/math] is always negative (since [math]\displaystyle{ x \to 0^- }[/math] means that [math]\displaystyle{ x \to 0 }[/math] with all values of [math]\displaystyle{ x }[/math] satisfying [math]\displaystyle{ x \lt 0 }[/math]), which implies that [math]\displaystyle{ - 1/x }[/math] is always positive so that [math]\displaystyle{ \lim_{x \to 0^-} {-1/x} }[/math] diverges[note 1] to [math]\displaystyle{ + \infty }[/math] (and not to [math]\displaystyle{ - \infty }[/math]) as [math]\displaystyle{ x }[/math] approaches [math]\displaystyle{ 0 }[/math] from the left. Similarly, [math]\displaystyle{ \lim_{x \to 0^+} {-1/x} = - \infty }[/math] since all values of [math]\displaystyle{ x }[/math] satisfy [math]\displaystyle{ x \gt 0 }[/math] (said differently, [math]\displaystyle{ x }[/math] is always positive) as [math]\displaystyle{ x }[/math] approaches [math]\displaystyle{ 0 }[/math] from the right, which implies that [math]\displaystyle{ - 1/x }[/math] is always negative so that [math]\displaystyle{ \lim_{x \to 0^+} {-1/x} }[/math] diverges to [math]\displaystyle{ - \infty. }[/math]
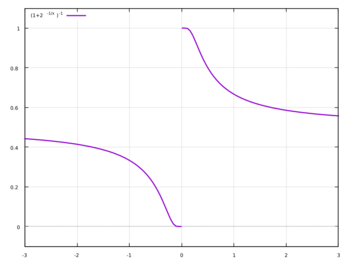
Example 2: One example of a function with different one-sided limits is [math]\displaystyle{ f(x) = \frac{1}{1 + 2^{-1/x}}, }[/math] (cf. picture) where the limit from the left is [math]\displaystyle{ \lim_{x \to 0^-} f(x) = 0 }[/math] and the limit from the right is [math]\displaystyle{ \lim_{x \to 0^+} f(x) = 1. }[/math] To calculate these limits, first show that [math]\displaystyle{ \lim_{x \to 0^-} 2^{-1/x} = \infty \qquad \text{ and } \qquad \lim_{x \to 0^+} 2^{-1/x} = 0 }[/math] (which is true because [math]\displaystyle{ \lim_{x \to 0^-} {-1/x} = + \infty \text{ and } \lim_{x \to 0^+} {-1/x} = - \infty }[/math]) so that consequently, [math]\displaystyle{ \lim_{x \to 0^+} \frac{1}{1 + 2^{-1/x}} = \frac{1}{1 + \displaystyle\lim_{x \to 0^+} 2^{-1/x}} = \frac{1}{1 + 0} = 1 }[/math] whereas [math]\displaystyle{ \lim_{x \to 0^-} \frac{1}{1 + 2^{-1/x}} = 0 }[/math] because the denominator diverges to infinity; that is, because [math]\displaystyle{ \lim_{x \to 0^-} 1 + 2^{-1/x} = \infty. }[/math] Since [math]\displaystyle{ \lim_{x \to 0^-} f(x) \neq \lim_{x \to 0^+} f(x), }[/math] the limit [math]\displaystyle{ \lim_{x \to 0} f(x) }[/math] does not exist.
Relation to topological definition of limit
The one-sided limit to a point [math]\displaystyle{ p }[/math] corresponds to the general definition of limit, with the domain of the function restricted to one side, by either allowing that the function domain is a subset of the topological space, or by considering a one-sided subspace, including [math]\displaystyle{ p. }[/math][1][verification needed] Alternatively, one may consider the domain with a half-open interval topology.[citation needed]
Abel's theorem
A noteworthy theorem treating one-sided limits of certain power series at the boundaries of their intervals of convergence is Abel's theorem.[citation needed]
Notes
- ↑ A limit that is equal to [math]\displaystyle{ \infty }[/math] is said to diverge to [math]\displaystyle{ \infty }[/math] rather than converge to [math]\displaystyle{ \infty. }[/math] The same is true when a limit is equal to [math]\displaystyle{ - \infty. }[/math]
References
- ↑ 1.0 1.1 1.2 1.3 "One-sided limit - Encyclopedia of Mathematics". https://encyclopediaofmath.org/wiki/One-sided_limit.
- ↑ 2.0 2.1 2.2 Fridy, J. A. (24 January 2020) (in en). Introductory Analysis: The Theory of Calculus. Gulf Professional Publishing. pp. 48. ISBN 978-0-12-267655-0. https://books.google.com/books?id=SaZYs-OKqJcC&dq=%22one-sided+limit%22&pg=PA48. Retrieved 7 August 2021.
- ↑ Hasan, Osman; Khayam, Syed (2014-01-02). "Towards Formal Linear Cryptanalysis using HOL4" (in en). Journal of Universal Computer Science 20 (2): 209. doi:10.3217/jucs-020-02-0193. ISSN 0948-6968. https://www.jucs.org/jucs_20_2/towards_formal_linear_cryptanalysis/jucs_20_02_0193_0212_hasan.pdf.
- ↑ Gasic, Andrei G. (2020-12-12). Phase Phenomena of Proteins in Living Matter (Thesis thesis).
- ↑ Brokate, Martin; Manchanda, Pammy; Siddiqi, Abul Hasan (2019), "Limit and Continuity" (in en), Calculus for Scientists and Engineers, Industrial and Applied Mathematics (Singapore: Springer Singapore): pp. 39–53, doi:10.1007/978-981-13-8464-6_2, ISBN 978-981-13-8463-9, http://link.springer.com/10.1007/978-981-13-8464-6_2, retrieved 2022-01-11
- ↑ Giv, Hossein Hosseini (28 September 2016) (in en). Mathematical Analysis and Its Inherent Nature. American Mathematical Soc.. pp. 130. ISBN 978-1-4704-2807-5. https://books.google.com/books?id=Hf0mDQAAQBAJ&q=%22one-sided+limit%22. Retrieved 7 August 2021.
See also
 |