Chemistry:Buckingham potential
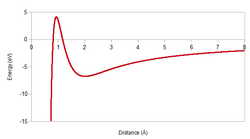
In theoretical chemistry, the Buckingham potential is a formula proposed by Richard Buckingham which describes the Pauli exclusion principle and van der Waals energy [math]\displaystyle{ \Phi_{12}(r) }[/math] for the interaction of two atoms that are not directly bonded as a function of the interatomic distance [math]\displaystyle{ r }[/math]. It is a variety of interatomic potentials.
- [math]\displaystyle{ \Phi_{12}(r) = A \exp \left(-Br\right) - \frac{C}{r^6} }[/math]
Here, [math]\displaystyle{ A }[/math], [math]\displaystyle{ B }[/math] and [math]\displaystyle{ C }[/math] are constants. The two terms on the right-hand side constitute a repulsion and an attraction, because their first derivatives with respect to [math]\displaystyle{ r }[/math] are negative and positive, respectively.
Buckingham proposed this as a simplification of the Lennard-Jones potential, in a theoretical study of the equation of state for gaseous helium, neon and argon.[1]
As explained in Buckingham's original paper and, e.g., in section 2.2.5 of Jensen's text,[2] the repulsion is due to the interpenetration of the closed electron shells. "There is therefore some justification for choosing the repulsive part (of the potential) as an exponential function". The Buckingham potential has been used extensively in simulations of molecular dynamics.
Because the exponential term converges to a constant as [math]\displaystyle{ r }[/math]→[math]\displaystyle{ 0 }[/math], while the [math]\displaystyle{ r^{-6} }[/math] term diverges, the Buckingham potential becomes attractive as [math]\displaystyle{ r }[/math] becomes small. This may be problematic when dealing with a structure with very short interatomic distances, as any nuclei that cross a certain threshold will become strongly (and unphysically) bound to one another at a distance of zero.[2]
Modified Buckingham (Exp-Six) potential
The modified Buckingham potential, also called the "exp-six" potential, is used to calculate the interatomic forces for gases based on Chapman and Cowling collision theory.[3] The potential has the form
[math]\displaystyle{ \Phi_{12}(r) = \frac{\epsilon}{1-6/\alpha}\left[ \frac6\alpha \exp \left[\alpha\left(1-\frac{r}{r_{min}}\right)\right] - \left(\frac{r_{min}}{r}\right)^6\right] }[/math]
where [math]\displaystyle{ \Phi_{12}(r) }[/math] is the interatomic potential between atom i and atom j, [math]\displaystyle{ \epsilon }[/math] is the minimum potential energy, [math]\displaystyle{ \alpha }[/math] is the measurement of the repulsive energy steepness which is the ratio [math]\displaystyle{ \sigma/r_{min} }[/math], [math]\displaystyle{ \sigma }[/math] is the value of [math]\displaystyle{ r }[/math] where [math]\displaystyle{ \Phi_{12}(r) }[/math] is zero, and [math]\displaystyle{ r_{min} }[/math] is the value of [math]\displaystyle{ r }[/math] which can achieve the minimum interatomic potential [math]\displaystyle{ \epsilon }[/math]. This potential function is only valid when [math]\displaystyle{ r\gt r_{max} }[/math], as the potential will decay towards [math]\displaystyle{ -\infty }[/math] as [math]\displaystyle{ r \rightarrow 0 }[/math]. This is corrected by identifying [math]\displaystyle{ r_{max} }[/math], which is the value of [math]\displaystyle{ r }[/math] at which the potential is maximized; when [math]\displaystyle{ r\leq{r_{max}} }[/math], the potential is set to infinity.
Coulomb–Buckingham potential
The Coulomb–Buckingham potential is an extension of the Buckingham potential for application to ionic systems (e.g. ceramic materials). The formula for the interaction is
- [math]\displaystyle{ \Phi_{12}(r) = A \exp \left(-Br\right) - \frac{C}{r^6} + \frac{q_1q_2}{4\pi\varepsilon_0 r} }[/math]
where A, B, and C are suitable constants and the additional term is the electrostatic potential energy.
The above equation may be written in its alternate form as
- [math]\displaystyle{ \Phi(r) = \varepsilon \left\{ \frac{6}{\alpha-6}\exp \left(\alpha\left[1-\frac{r}{r_0}\right]\right) - \frac{\alpha}{\alpha-6} \left(\frac{r_0}{r}\right)^6 \right\}+ \frac{q_1q_2}{4\pi\varepsilon_0 r} }[/math]
where [math]\displaystyle{ r_0 }[/math] is the minimum energy distance, [math]\displaystyle{ \alpha }[/math] is a free dimensionless parameter and [math]\displaystyle{ \varepsilon }[/math] is the depth of the minimum energy.
Beest Kramer van Santen (BKS) potential
The BKS potential is a force field that may be used to simulate the interatomic potential between Silica glass atoms.[4] Rather than relying only on experimental data, the BKS potential is derived by combining ab initio quantum chemistry methods on small silica clusters to describe accurate interaction between nearest-neighbors, which is the function of accurate force field. The experimental data is applied to fit larger scale force information beyond nearest neighbors. By combining the microscopic and macroscopic information, the applicability of the BKS potential has been extended to both the silica polymorphs and other tetrahedral network oxides systems systems that have same cluster structure, such as aluminophosphates, carbon and silicon.
The form of this interatomic potential is the usual Buckingham form, with the addition of a Coulomb force term. The formula for the BKS potential is expressed as
- [math]\displaystyle{ \Phi_{12}(r) = \left[ A_{12} \exp \left(-B_{12}r_{12}\right) - \frac{C_{12}}{r_{12}^6}\right] + \frac{q_1q_2}{r_{12}} }[/math]
where [math]\displaystyle{ \Phi_{12}(r) }[/math] is the interatomic potential between atom i and atom j, [math]\displaystyle{ q_1 }[/math]and [math]\displaystyle{ q_2 }[/math] are the charges magnitudes, [math]\displaystyle{ r_{12} }[/math] is the distance between atoms, and [math]\displaystyle{ A_{ij} }[/math],[math]\displaystyle{ B_{ij} }[/math] and [math]\displaystyle{ C_{ij} }[/math] are constant parameters based on the type of atoms.[5]
The BKS potential parameters for common atoms are shown below:[5]
| i-j | Aij(eV) | Bij(Å−1) | Cij(eV•Å6) |
|---|---|---|---|
| O - O | 1388.7730 | 2.76000 | 175.0000 |
| O - Si | 18,003.757 | 4.87318 | 133.5381 |
| Si - Si | 0 | 0 | 0 |
| Al - O | 16,008.5345 | 4.79667 | 130.5659 |
| Al - Al | 0 | 0 | 0 |
| P - O | 9,034.2080 | 5.19098 | 19.8793 |
| P - P | 0 | 0 | 0 |
An updated version of the BKS potential introduced a new repulsive term to prevent atom overlapping.[6] The modified potential is taken as
[math]\displaystyle{ \Phi_{12}(r) = \left[ A_{12} \exp \left(-B_{12}r_{12}\right) - \frac{C_{12}}{r_{12}^6}\right] + \frac{q_1q_2}{r_{12}} + \frac{D_{12}}{r_{12}^{24}} }[/math]
where the constant parameters [math]\displaystyle{ D_{ij} }[/math] were chosen to have the following values for Silica glass:
| Si - Si | Si - O | O - O | |
|---|---|---|---|
| Dij(eV•Å24) | 3423200 | 29 | 113 |
References
- ↑ Buckingham, R. A. (1938). "The Classical Equation of State of Gaseous Helium, Neon and Argon". Proceedings of the Royal Society A 168 (933): 264–283. doi:10.1098/rspa.1938.0173. Bibcode: 1938RSPSA.168..264B.
- ↑ 2.0 2.1 F. Jensen, Introduction to Computational Chemistry, 2nd ed., Wiley, 2007,
- ↑ Mason, Edward A. (2004-12-29). "Transport Properties of Gases Obeying a Modified Buckingham (Exp‐Six) Potential" (in en). The Journal of Chemical Physics 22 (2): 169–186. doi:10.1063/1.1740026. ISSN 0021-9606. https://aip.scitation.org/doi/abs/10.1063/1.1740026.
- ↑ van Beest, B. W. H.; Kramer, G. J.; van Santen, R. A. (1990-04-16). "Force fields for silicas and aluminophosphates based onab initiocalculations". Physical Review Letters 64 (16): 1955–1958. doi:10.1103/physrevlett.64.1955. ISSN 0031-9007. PMID 10041537. Bibcode: 1990PhRvL..64.1955V. https://journals.aps.org/prl/pdf/10.1103/PhysRevLett.64.1955.
- ↑ 5.0 5.1 Kramer, G. J.; Farragher, N. P.; van Beest, B. W. H.; van Santen, R. A. (1991-02-15). "Interatomic force fields for silicas, aluminophosphates, and zeolites: Derivation based onab initiocalculations". Physical Review B 43 (6): 5068–5080. doi:10.1103/physrevb.43.5068. ISSN 0163-1829. PMID 9997885. Bibcode: 1991PhRvB..43.5068K. https://journals.aps.org/prb/pdf/10.1103/PhysRevB.43.5068.
- ↑ Carré, Antoine; Ispas, Simona; Horbach, Jürgen; Kob, Walter (2016-11-01). "Developing empirical potentials from ab initio simulations: The case of amorphous silica" (in en). Computational Materials Science 124: 323–334. doi:10.1016/j.commatsci.2016.07.041. ISSN 0927-0256. https://www.sciencedirect.com/science/article/pii/S0927025616303688.
External links
 |