Compound of six decagonal prisms

Short description: Polyhedral compound

Compound of six decagonal prisms
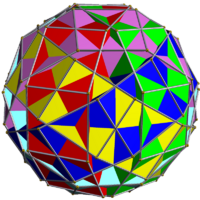
Type	Uniform compound
Index	UC40
Polyhedra	6 decagonal prisms
Faces	12 decagons, 60 squares
Edges	180
Vertices	120
Symmetry group	icosahedral (Ih)
Subgroup restricting to one constituent	5-fold antiprismatic (D5d)

This uniform polyhedron compound is a symmetric arrangement of 6 decagonal prisms, aligned with the axes of fivefold rotational symmetry of a dodecahedron.

Cartesian coordinates

Cartesian coordinates for the vertices of this compound are all the cyclic permutations of

(±√(τ⁻¹/√5), ±2τ, ±√(τ/√5))

(±(√(τ⁻¹/√5)−τ²), ±1, ±(√(τ/√5)+τ))

(±(√(τ⁻¹/√5)−τ), ±τ², ±(√(τ/√5)+1))

(±(√(τ⁻¹/√5)+τ), ±τ², ±(√(τ/√5)−1))

(±(√(τ⁻¹/√5)+τ²), ±1, ±(√(τ/√5)−τ))

where τ = (1+√5)/2 is the golden ratio (sometimes written φ).

References

• Skilling, John (1976), "Uniform Compounds of Uniform Polyhedra", Mathematical Proceedings of the Cambridge Philosophical Society 79 (3): 447–457, doi:10.1017/S0305004100052440, Bibcode: 1976MPCPS..79..447S .