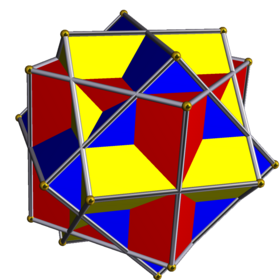
Compound of three cubes
| Compound of three cubes | |
|---|---|
| |
| Type | Uniform compound |
| Index | UC8 |
| Convex hull | Nonuniform truncated octahedron |
| Polyhedra | 3 cubes |
| Faces | 6+12 squares |
| Edges | 36 |
| Vertices | 24 |
| Symmetry group | octahedral (Oh) |
| Subgroup restricting to one constituent | 4-fold prismatic (D4h) |
In geometry, the compound of three cubes is a uniform polyhedron compound formed from three cubes arranged with octahedral symmetry.[1] It has been depicted in works by Max Brückner and M.C. Escher.
History
This compound appears in Max Brückner's book Vielecke und Vielflache (1900),[2] and in the lithograph print Waterfall (1961) by M.C. Escher, who learned of it from Brückner's book. Its dual, the compound of three octahedra, forms the central image in an earlier Escher woodcut, Stars.[3]
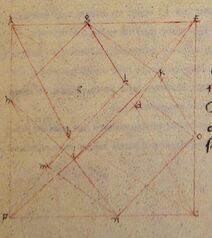
In the 15th-century manuscript De quinque corporibus regularibus, Piero della Francesca includes a drawing of an octahedron circumscribed around a cube, with eight of the cube edges lying in the octahedron's eight faces. Three cubes inscribed in this way within a single octahedron would form the compound of three cubes, but della Francesca does not depict the compound.[4]
Construction and coordinates
This compound can be constructed by superimposing three identical cubes, and then rotating each by 45 degrees about a separate axis (that passes through the centres of two opposite faces).[3]
Cartesian coordinates for the vertices of this compound can be chosen as all the permutations of [math]\displaystyle{ (0,\pm 1,\pm\sqrt{2}) }[/math].
References
- ↑ Verheyen, Hugo F. (1996), "Chapter 4: Classification of the finite compounds of cubes", Symmetry Orbits, Design Science Collection, Boston: Birkhäuser, pp. 95–159, doi:10.1007/978-1-4612-4074-7_5, ISBN 0-8176-3661-7; see in particular p. 136.
- ↑ Brückner, Max (1900), Vielecke und Vielflache, Theorie und Geschichte, Leipzig: B.G. Teubner, Plate 23
- ↑ Jump up to: 3.0 3.1 Hart, George W., "Max Brücknerʼs Wunderkammer of Paper Polyhedra", Bridges 2019 Conference Proceedings, pp. 59–66, http://archive.bridgesmathart.org/2019/bridges2019-59.pdf
- ↑ Hart, George W. (1998), "Piero della Francesca's Polyhedra", Virtual Polyhedra, http://www.georgehart.com/virtual-polyhedra/piero.html.
 |