Conformally flat manifold

The upper manifold is flat. The lower one is not, but it is conformal to the first one

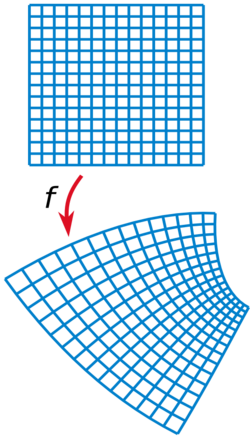
A (pseudo-)Riemannian manifold is conformally flat if each point has a neighborhood that can be mapped to flat space by a conformal transformation.

In practice, the metric tensor $g$ of the manifold $M$ has to be conformal to the flat metric tensor $\eta$, i.e., the geodesics maintain in all points of $M$ the angles by moving from one to the other, as well as keeping the null geodesics unchanged, that means there exists a function $\lambda (x)$ such that $g(x)={\lambda }^2(x)\eta$, where $\lambda (x)$ is known as the conformal factor and $x$ is a point on the manifold.

More formally, let $(M,g)$ be a pseudo-Riemannian manifold. Then $(M,g)$ is conformally flat if for each point $x$ in $M$, there exists a neighborhood $U$ of $x$ and a smooth function $f$ defined on $U$ such that $(U,e^{2f}g)$ is flat (i.e. the curvature of $e^{2f}g$ vanishes on $U$). The function $f$ need not be defined on all of $M$.

Some authors use the definition of locally conformally flat when referred to just some point $x$ on $M$ and reserve the definition of conformally flat for the case in which the relation is valid for all $x$ on $M$.

Examples

• Every manifold with constant sectional curvature is conformally flat.
• Every 2-dimensional pseudo-Riemannian manifold is conformally flat.
  • The line element of the two dimensional spherical coordinates, like the one used in the geographic coordinate system, $d{s}^2=d{\theta }^2+{\sin }^2\theta d{\varphi }^2$, has metric tensor $g_{ik}=\left[\begin{array}{cc}1& 0\\ 0& {\sin }^2\theta \end{array}\right]$ and is not flat but with the stereographic projection can be mapped to a flat space using the conformal factor $\frac{2}{1+r^2}$, where $r$ is the distance from the origin of the flat space, obtaining $d{s}^2=d{\theta }^2+{\sin }^2\theta d{\varphi }^2=\frac{4}{(1+r^2{)}^2}(d{x}^2+d{y}^2)$.
• A 3-dimensional pseudo-Riemannian manifold is conformally flat if and only if the Cotton tensor vanishes.
• An n-dimensional pseudo-Riemannian manifold for n ≥ 4 is conformally flat if and only if the Weyl tensor vanishes.
• Every compact, simply connected, conformally Euclidean Riemannian manifold is conformally equivalent to the round sphere.

• The stereographic projection provides a coordinate system for the sphere in which conformal flatness is explicit, as the metric is proportional to the flat one.

• In general relativity, conformally flat manifolds are often used, for instance, in describing the Friedmann–Lemaître–Robertson–Walker metric. However, this is not always possible, as in the case of the Kerr metric, which does not admit any conformally flat slices. : An example of conformally flat metric can be obtained by transforming the Kruskal–Szekeres coordinates for the Schwarzschild metric, which have line element $d{s}^2=(1-2GM/r)dvdu$ with metric tensor $g_{ik}=\left[\begin{array}{cc}0& 1-2GM/r\\ 1-2GM/r& 0\end{array}\right]$ and so is not flat. But with the transformations $t=(v+u)/2$ and $x=(v-u)/2$ becomes $d{s}^2=(1-2GM/r)(d{t}^2-d{x}^2)$ with metric tensor $g_{ik}=\left[\begin{array}{cc}1-2GM/r& 0\\ 0& -1+2GM/r\end{array}\right]$, which is the flat metric times the conformal factor $1-2GM/r$.

See also

• Weyl–Schouten theorem
• Conformal geometry
• Yamabe problem