n-sphere

Short description: Generalized sphere of dimension n (mathematics)

2-sphere wireframe as an orthogonal projection

Just as a stereographic projection can project a sphere's surface to a plane, it can also project a 3-sphere into 3-space. This image shows three coordinate directions projected to 3-space: parallels (red), meridians (blue) and hypermeridians (green). Due to the conformal property of the stereographic projection, the curves intersect each other orthogonally (in the yellow points) as in 4D. All of the curves are circles: the curves that intersect ⟨0,0,0,1⟩ have an infinite radius (= straight line).

In mathematics, an n-sphere or hypersphere is an n-dimensional generalization of the 1-dimensional circle and 2-dimensional sphere to any non-negative integer n. The n-sphere is the setting for n-dimensional spherical geometry.

Considered extrinsically, as a hypersurface embedded in (n + 1)-dimensional Euclidean space, an n-sphere is the locus of points at equal distance (the radius) from a given center point. Its interior, consisting of all points closer to the center than the radius, is an (n + 1)-dimensional ball. In particular:

• The 0-sphere is the pair of points at the ends of a line segment (1-ball).
• The 1-sphere is a circle, the circumference of a disk (2-ball) in the two-dimensional plane.
• The 2-sphere, often simply called a sphere, is the boundary of a 3-ball in three-dimensional space.
• The 3-sphere is the boundary of a 4-ball in four-dimensional space.
• The (n – 1)-sphere is the boundary of an n-ball.

Given a Cartesian coordinate system, the unit n-sphere of radius 1 can be defined as:

[math]\displaystyle{ S^n = \left\{ x \in \mathbb{R}^{n+1} : \left\| x \right\| = 1 \right\}. }[/math]

Considered intrinsically, when n ≥ 1, the n-sphere is a Riemannian manifold of positive constant curvature, and is orientable. The geodesics of the n-sphere are called great circles.

The stereographic projection maps the n-sphere onto n-space with a single adjoined point at infinity; under the metric thereby defined, [math]\displaystyle{ \R^n \cup \{\infty\} }[/math] is a model for the n-sphere.

In the more general setting of topology, any topological space that is homeomorphic to the unit n-sphere is called an n-sphere. Under inverse stereographic projection, the n-sphere is the one-point compactification of n-space. The n-spheres admit several other topological descriptions: for example, they can be constructed by gluing two n-dimensional spaces together, by identifying the boundary of an n-cube with a point, or (inductively) by forming the suspension of an (n − 1)-sphere. When n ≥ 2 it is simply connected; the 1-sphere (circle) is not simply connected; the 0-sphere is not even connected, consisting of two discrete points.

Description

For any natural number n, an n-sphere of radius r is defined as the set of points in (n + 1)-dimensional Euclidean space that are at distance r from some fixed point c, where r may be any positive real number and where c may be any point in (n + 1)-dimensional space. In particular:

• a 0-sphere is a pair of points {c − r, c + r}, and is the boundary of a line segment (1-ball).
• a 1-sphere is a circle of radius r centered at c, and is the boundary of a disk (2-ball).
• a 2-sphere is an ordinary 2-dimensional sphere in 3-dimensional Euclidean space, and is the boundary of an ordinary ball (3-ball).
• a 3-sphere is a 3-dimensional sphere in 4-dimensional Euclidean space.

Cartesian coordinates

The set of points in (n + 1)-space, (x₁, x₂, ..., x_n+1), that define an n-sphere, Sⁿ(r), is represented by the equation:

[math]\displaystyle{ r^2=\sum_{i=1}^{n+1} (x_i - c_i)^2 , }[/math]

where c = (c₁, c₂, ..., c_n+1) is a center point, and r is the radius.

The above n-sphere exists in (n + 1)-dimensional Euclidean space and is an example of an n-manifold. The volume form ω of an n-sphere of radius r is given by

[math]\displaystyle{ \omega = \frac{1}{r} \sum_{j=1}^{n+1} (-1)^{j-1} x_j \,dx_1 \wedge \cdots \wedge dx_{j-1} \wedge dx_{j+1}\wedge \cdots \wedge dx_{n+1} = {\star} dr }[/math]

where [math]\displaystyle{ {\star} }[/math] is the Hodge star operator; see (Flanders 1989) for a discussion and proof of this formula in the case r = 1. As a result,

[math]\displaystyle{ dr \wedge \omega = dx_1 \wedge \cdots \wedge dx_{n+1}. }[/math]

n-ball

The space enclosed by an n-sphere is called an (n + 1)-ball. An (n + 1)-ball is closed if it includes the n-sphere, and it is open if it does not include the n-sphere.

Specifically:

• A 1-ball, a line segment, is the interior of a 0-sphere.
• A 2-ball, a disk, is the interior of a circle (1-sphere).
• A 3-ball, an ordinary ball, is the interior of a sphere (2-sphere).
• A 4-ball is the interior of a 3-sphere, etc.

Topological description

Topologically, an n-sphere can be constructed as a one-point compactification of n-dimensional Euclidean space. Briefly, the n-sphere can be described as Sⁿ = ℝⁿ ∪ {∞}, which is n-dimensional Euclidean space plus a single point representing infinity in all directions. In particular, if a single point is removed from an n-sphere, it becomes homeomorphic to ℝⁿ. This forms the basis for stereographic projection.

Volume and area

Let S_n−1 be the surface area of the unit (n − 1)-sphere of radius 1 embedded in n-dimensional Euclidean space, and let V_n be the volume of its interior, the unit n-ball. The surface area of an arbitrary (n − 1)-sphere is proportional to the (n − 1)st power of the radius, and the volume of an arbitrary n-ball is proportional to the nth power of the radius.

Graphs of volumes (V_n) and surface areas (S_n−1) of n-balls of radius 1.

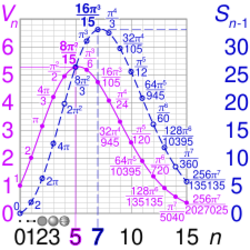
The 0-ball is sometimes defined as a single point. The 0-dimensional Hausdorff measure is the number of points in a set. So

[math]\displaystyle{ V_0=1. }[/math]

A unit 1-ball is a line segment whose points have a single coordinate in the interval [−1, 1] of length 2, and the 0-sphere consists of its two end-points, with coordinate {−1, 1}.

[math]\displaystyle{ S_0 = 2, \quad V_1 = 2. }[/math]

A unit 1-sphere is the unit circle in the Euclidean plane, and its interior is the unit disk (2-ball).

[math]\displaystyle{ S_1 = 2\pi, \quad V_2 = \pi . }[/math]

The interior of a 2-sphere in three-dimensional space is the unit 3-ball.

[math]\displaystyle{ S_2 = 4\pi, \quad V_3 = \tfrac{4}{3} \pi. }[/math]

In general, S_n−1 and V_n are given in closed form by the expressions

[math]\displaystyle{ S_{n-1} = \frac{2 \pi^{n/2}}{\Gamma\bigl(\frac{n}{2}\bigr)}, \quad V_n = \frac{\pi^{n/2}}{\Gamma\bigl(\frac{n}{2} + 1\bigr)} }[/math]

where Γ is the gamma function.

As n tends to infinity, the volume of the unit n-ball (ratio between the volume of an n-ball of radius 1 and an n-cube of side length 1) tends to zero.

Recurrences

The surface area, or properly the n-dimensional volume, of the n-sphere at the boundary of the (n + 1)-ball of radius R is related to the volume of the ball by the differential equation

[math]\displaystyle{ S_{n}R^{n}=\frac{dV_{n+1}R^{n+1}}{dR}={(n+1)V_{n+1}R^{n}}. }[/math]

Equivalently, representing the unit n-ball as a union of concentric (n − 1)-sphere shells,

[math]\displaystyle{ V_{n+1} = \int_0^1 S_{n}r^{n}\,dr = \frac{1}{n+1}S_n. }[/math]

We can also represent the unit (n + 2)-sphere as a union of products of a circle (1-sphere) with an n-sphere. Then [math]\displaystyle{ S_{n+2} = 2\pi V_{n+1}. }[/math] Since S₁ = 2π V₀, the equation

[math]\displaystyle{ S_{n+1} = 2\pi V_{n} }[/math]

holds for all n. Along with the base cases [math]\displaystyle{ S_0 = 2, }[/math] [math]\displaystyle{ V_1 = 2 }[/math] from above, these recurrences can be used to compute the surface area of any sphere or volume of any ball.

Spherical coordinates

We may define a coordinate system in an n-dimensional Euclidean space which is analogous to the spherical coordinate system defined for 3-dimensional Euclidean space, in which the coordinates consist of a radial coordinate r, and n − 1 angular coordinates φ₁, φ₂, ..., φ_n−1, where the angles φ₁, φ₂, ..., φ_n−2 range over [0, π] radians (or over [0, 180] degrees) and φ_n−1 ranges over [0, 2π) radians (or over [0, 360) degrees). If x_i are the Cartesian coordinates, then we may compute x₁, ..., x_n from r, φ₁, ..., φ_n−1 with:

[math]\displaystyle{ \begin{align} x_1 &= r \cos(\varphi_1), \\[5mu] x_2 &= r \sin(\varphi_1) \cos(\varphi_2), \\[5mu] x_3 &= r \sin(\varphi_1) \sin(\varphi_2) \cos(\varphi_3), \\ &\qquad \vdots\\ x_{n-1} &= r \sin(\varphi_1) \cdots \sin(\varphi_{n-2}) \cos(\varphi_{n-1}), \\[5mu] x_n &= r \sin(\varphi_1) \cdots \sin(\varphi_{n-2}) \sin(\varphi_{n-1}). \end{align} }[/math]

Except in the special cases described below, the inverse transformation is unique:

[math]\displaystyle{ \begin{align} r &= {\textstyle \sqrt{{x_n}^2 + {x_{n-1}}^2 + \cdots + {x_2}^2 + {x_1}^2}}, \\[5mu] \varphi_1 &= \operatorname{atan2} \left({\textstyle \sqrt{{x_n}^2 + {x_{n-1}}^2 + \cdots + {x_2}^2}}, x_{1}\right), \\[5mu] \varphi_2 &= \operatorname{atan2} \left({\textstyle \sqrt{{x_n}^2 + {x_{n-1}}^2 + \cdots + {x_3}^2}}, x_{2}\right), \\ &\qquad \vdots\\ \varphi_{n-2} &= \operatorname{atan2} \left({\textstyle \sqrt{{x_n}^2 + {x_{n-1}}^2}}, x_{n-2}\right), \\[5mu] \varphi_{n-1} &= \operatorname{atan2} \left(x_n, x_{n-1}\right). \end{align} }[/math]

where atan2 is the two-argument arctangent function.

There are some special cases where the inverse transform is not unique; φ_k for any k will be ambiguous whenever all of x_k, x_k+1, ... x_n are zero; in this case φ_k may be chosen to be zero. (For example, for the 2-sphere, when the polar angle is 0 or π then the point is one of the poles, zenith or nadir, and the choice of azimuthal angle is arbitrary.)

Spherical volume and area elements

To express the volume element of n-dimensional Euclidean space in terms of spherical coordinates, let [math]\displaystyle{ s_k = \sin \varphi_k }[/math] and [math]\displaystyle{ c_k = \cos \varphi_k }[/math] for concision, then observe that the Jacobian matrix of the transformation is:

[math]\displaystyle{ J_n = \begin{pmatrix} c_1 &-rs_1 &0 &0 &\cdots &0 \\ s_1c_2 &rc_1c_2 &-rs_1s_2 &0 &\cdots &0 \\ \vdots &\vdots & \vdots & &\ddots &\vdots \\ & & & & &0 \\ s_1\cdots s_{n-2}c_{n-1} &\cdots &\cdots & & &-rs_1\cdots s_{n-2}s_{n-1} \\ s_{1}\cdots s_{n-2}s_{n-1} &rc_1\cdots s_{n-1} &\cdots & & &\phantom{-}rs_1\cdots s_{n-2}c_{n-1} \end{pmatrix}. }[/math]

The determinant of this matrix can be calculated by induction. When n = 2, a straightforward computation shows that the determinant is r. For larger n, observe that J_n can be constructed from J_n−1 as follows. Except in column n, rows n − 1 and n of J_n are the same as row n − 1 of J_n−1, but multiplied by an extra factor of cos φ_n−1 in row n − 1 and an extra factor of sin φ_n−1 in row n. In column n, rows n − 1 and n of J_n are the same as column n − 1 of row n − 1 of J_n−1, but multiplied by extra factors of sin φ_n−1 in row n − 1 and cos φ_n−1 in row n, respectively. The determinant of J_n can be calculated by Laplace expansion in the final column. By the recursive description of J_n, the submatrix formed by deleting the entry at (n − 1, n) and its row and column almost equals J_n−1, except that its last row is multiplied by sin φ_n−1. Similarly, the submatrix formed by deleting the entry at (n, n) and its row and column almost equals J_n−1, except that its last row is multiplied by cos φ_n−1. Therefore the determinant of J_n is

[math]\displaystyle{ \begin{align} |J_n| &= (-1)^{(n-1)+n}(-rs_1 \dotsm s_{n-2}s_{n-1})(s_{n-1}|J_{n-1}|) \\ &\qquad {}+ (-1)^{n+n}(rs_1 \dotsm s_{n-2}c_{n-1})(c_{n-1}|J_{n-1}|) \\ &= (rs_1 \dotsm s_{n-2}|J_{n-1}|(s_{n-1}^2 + c_{n-1}^2) \\ &= (rs_1 \dotsm s_{n-2})|J_{n-1}|. \end{align} }[/math]

Induction then gives a closed-form expression for the volume element in spherical coordinates

[math]\displaystyle{ \begin{align} d^nV &= \left|\det\frac{\partial (x_i)}{\partial\left(r,\varphi_j\right)}\right| dr\,d\varphi_1 \, d\varphi_2\cdots d\varphi_{n-1} \\ &= r^{n-1}\sin^{n-2}(\varphi_1)\sin^{n-3}(\varphi_2)\cdots \sin(\varphi_{n-2})\, dr\,d\varphi_1 \, d\varphi_2\cdots d\varphi_{n-1}. \end{align} }[/math]

The formula for the volume of the n-ball can be derived from this by integration.

Similarly the surface area element of the (n − 1)-sphere of radius R, which generalizes the area element of the 2-sphere, is given by

[math]\displaystyle{ d_{S^{n-1}}V = R^{n-1}\sin^{n-2}(\varphi_1)\sin^{n-3}(\varphi_2)\cdots \sin(\varphi_{n-2})\, d\varphi_1 \, d\varphi_2\cdots d\varphi_{n-1}. }[/math]

The natural choice of an orthogonal basis over the angular coordinates is a product of ultraspherical polynomials,

[math]\displaystyle{ \begin{align} & {} \quad \int_0^\pi \sin^{n-j-1}\left(\varphi_j\right) C_s^{\left(\frac{n-j-1}{2}\right)}\cos \left(\varphi_j \right)C_{s'}^{\left(\frac{n-j-1}{2}\right)}\cos \left(\varphi_j\right) \, d\varphi_j \\[6pt] & = \frac{2^{3-n+j}\pi \Gamma(s+n-j-1)}{s!(2s+n-j-1)\Gamma^2\left(\frac{n-j-1}{2}\right)}\delta_{s,s'} \end{align} }[/math]

for j = 1, 2, ..., n − 2, and the e^isφ_j for the angle j = n − 1 in concordance with the spherical harmonics.

Polyspherical coordinates

The standard spherical coordinate system arises from writing ℝⁿ as the product ℝ × ℝⁿ⁻¹. These two factors may be related using polar coordinates. For each point x of ℝⁿ, the standard Cartesian coordinates

[math]\displaystyle{ \mathbf{x} = (x_1, \dots, x_n) = (y_1, z_1, \dots, z_{n-1}) = (y_1, \mathbf{z}) }[/math]

can be transformed into a mixed polar–Cartesian coordinate system:

[math]\displaystyle{ \mathbf{x} = (r\sin\theta, (r\cos\theta)\hat\mathbf{z}). }[/math]

This says that points in ℝⁿ may be expressed by taking the ray starting at the origin and passing through [math]\displaystyle{ \hat\mathbf{z}=\mathbf{z}/\lVert\mathbf{z}\rVert\in S^{n-2} }[/math], rotating it towards [math]\displaystyle{ (1,0,\dots,0) }[/math] by [math]\displaystyle{ \theta=\arcsin y_1/r }[/math], and traveling a distance [math]\displaystyle{ r=\lVert\mathbf{x}\rVert }[/math] along the ray. Repeating this decomposition eventually leads to the standard spherical coordinate system.

Polyspherical coordinate systems arise from a generalization of this construction. The space ℝⁿ is split as the product of two Euclidean spaces of smaller dimension, but neither space is required to be a line. Specifically, suppose that p and q are positive integers such that n = p + q. Then ℝⁿ = ℝ^p × ℝ^q. Using this decomposition, a point x ∈ ℝⁿ may be written as

[math]\displaystyle{ \mathbf{x} = (x_1, \dots, x_n) = (y_1, \dots, y_p, z_1, \dots, z_q) = (\mathbf{y}, \mathbf{z}). }[/math]

This can be transformed into a mixed polar–Cartesian coordinate system by writing:

[math]\displaystyle{ \mathbf{x} = ((r\sin \theta)\hat\mathbf{y}, (r\cos \theta)\hat\mathbf{z}). }[/math]

Here [math]\displaystyle{ \hat\mathbf{y} }[/math] and [math]\displaystyle{ \hat\mathbf{z} }[/math] are the unit vectors associated to y and z. This expresses x in terms of [math]\displaystyle{ \hat\mathbf{y} \in S^{p-1} }[/math], [math]\displaystyle{ \hat\mathbf{z} \in S^{q-1} }[/math], r ≥ 0, and an angle θ. It can be shown that the domain of θ is [0, 2π) if p = q = 1, [0, π] if exactly one of p and q is 1, and [0, π/2] if neither p nor q are 1. The inverse transformation is

[math]\displaystyle{ \begin{align} r &= \lVert\mathbf{x}\rVert, \\ \theta &= \arcsin\frac{\lVert\mathbf{y}\rVert}{\lVert\mathbf{x}\rVert} = \arccos\frac{\lVert\mathbf{z}\rVert}{\lVert\mathbf{x}\rVert} = \arctan\frac{\lVert\mathbf{y}\rVert}{ \lVert\mathbf{z}\rVert}. \end{align} }[/math]

These splittings may be repeated as long as one of the factors involved has dimension two or greater. A polyspherical coordinate system is the result of repeating these splittings until there are no Cartesian coordinates left. Splittings after the first do not require a radial coordinate because the domains of [math]\displaystyle{ \hat\mathbf{y} }[/math] and [math]\displaystyle{ \hat\mathbf{z} }[/math] are spheres, so the coordinates of a polyspherical coordinate system are a non-negative radius and n − 1 angles. The possible polyspherical coordinate systems correspond to binary trees with n leaves. Each non-leaf node in the tree corresponds to a splitting and determines an angular coordinate. For instance, the root of the tree represents ℝⁿ, and its immediate children represent the first splitting into ℝ^p and ℝ^q. Leaf nodes correspond to Cartesian coordinates for Sⁿ⁻¹. The formulas for converting from polyspherical coordinates to Cartesian coordinates may be determined by finding the paths from the root to the leaf nodes. These formulas are products with one factor for each branch taken by the path. For a node whose corresponding angular coordinate is θ_i, taking the left branch introduces a factor of sin θ_i and taking the right branch introduces a factor of cos θ_i. The inverse transformation, from polyspherical coordinates to Cartesian coordinates, is determined by grouping nodes. Every pair of nodes having a common parent can be converted from a mixed polar–Cartesian coordinate system to a Cartesian coordinate system using the above formulas for a splitting.

Polyspherical coordinates also have an interpretation in terms of the special orthogonal group. A splitting ℝⁿ = ℝ^p × ℝ^q determines a subgroup

[math]\displaystyle{ \operatorname{SO}_p(\mathbb{R}) \times \operatorname{SO}_q(\mathbb{R}) \subseteq \operatorname{SO}_n(\mathbb{R}). }[/math]

This is the subgroup that leaves each of the two factors [math]\displaystyle{ S^{p-1} \times S^{q-1} \subseteq S^{n-1} }[/math] fixed. Choosing a set of coset representatives for the quotient is the same as choosing representative angles for this step of the polyspherical coordinate decomposition.

In polyspherical coordinates, the volume measure on ℝⁿ and the area measure on Sⁿ⁻¹ are products. There is one factor for each angle, and the volume measure on ℝⁿ also has a factor for the radial coordinate. The area measure has the form:

[math]\displaystyle{ dA_{n-1} = \prod_{i=1}^{n-1} F_i(\theta_i)\,d\theta_i, }[/math]

where the factors F_i are determined by the tree. Similarly, the volume measure is

[math]\displaystyle{ dV_n = r^{n-1}\,dr\,\prod_{i=1}^{n-1} F_i(\theta_i)\,d\theta_i. }[/math]

Suppose we have a node of the tree that corresponds to the decomposition ℝ^n₁+n₂ = ℝ^n₁ × ℝ^n₂ and that has angular coordinate θ. The corresponding factor F depends on the values of n₁ and n₂. When the area measure is normalized so that the area of the sphere is 1, these factors are as follows. If n₁ = n₂ = 1, then

[math]\displaystyle{ F(\theta) = \frac{d\theta}{2\pi}. }[/math]

If n₁ > 1 and n₂ = 1, and if B denotes the beta function, then

[math]\displaystyle{ F(\theta) = \frac{\sin^{n_1 - 1}\theta}{\Beta(\frac{n_1}{2}, \frac{1}{2})}\,d\theta. }[/math]

If n₁ = 1 and n₂ > 1, then

[math]\displaystyle{ F(\theta) = \frac{\cos^{n_2 - 1}\theta}{\Beta(\frac{1}{2}, \frac{n_2}{2})}\,d\theta. }[/math]

Finally, if both n₁ and n₂ are greater than one, then

[math]\displaystyle{ F(\theta) = \frac{(\sin^{n_1 - 1}\theta)(\cos^{n_2 - 1}\theta)}{\frac{1}{2}\Beta(\frac{n_1}{2}, \frac{n_2}{2})}\,d\theta. }[/math]

Stereographic projection

Just as a two-dimensional sphere embedded in three dimensions can be mapped onto a two-dimensional plane by a stereographic projection, an n-sphere can be mapped onto an n-dimensional hyperplane by the n-dimensional version of the stereographic projection. For example, the point [x,y,z] on a two-dimensional sphere of radius 1 maps to the point [x/1 − z, y/1 − z] on the xy-plane. In other words,

[math]\displaystyle{ [x,y,z] \mapsto \left[\frac{x}{1-z},\frac{y}{1-z}\right]. }[/math]

Likewise, the stereographic projection of an n-sphere Sⁿ of radius 1 will map to the (n − 1)-dimensional hyperplane ℝⁿ⁻¹ perpendicular to the x_n-axis as

[math]\displaystyle{ [x_1,x_2,\ldots,x_n] \mapsto \left[\frac{x_1}{1-x_n},\frac{x_2}{1-x_n},\ldots,\frac{x_{n-1}}{1-x_n}\right]. }[/math]

Probability distributions

Uniformly at random on the (n − 1)-sphere

A set of points drawn from a uniform distribution on the surface of a unit 2-sphere, generated using Marsaglia's algorithm.

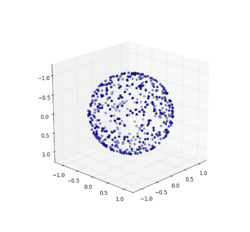
To generate uniformly distributed random points on the unit (n − 1)-sphere (that is, the surface of the unit n-ball), (Marsaglia 1972) gives the following algorithm.

Generate an n-dimensional vector of normal deviates (it suffices to use N(0, 1), although in fact the choice of the variance is arbitrary), x = (x₁, x₂, ..., x_n). Now calculate the "radius" of this point:

[math]\displaystyle{ r=\sqrt{x_1^2+x_2^2+\cdots+x_n^2}. }[/math]

The vector 1/rx is uniformly distributed over the surface of the unit n-ball.

An alternative given by Marsaglia is to uniformly randomly select a point x = (x₁, x₂, ..., x_n) in the unit n-cube by sampling each x_i independently from the uniform distribution over (–1, 1), computing r as above, and rejecting the point and resampling if r ≥ 1 (i.e., if the point is not in the n-ball), and when a point in the ball is obtained scaling it up to the spherical surface by the factor 1/r; then again 1/rx is uniformly distributed over the surface of the unit n-ball. This method becomes very inefficient for higher dimensions, as a vanishingly small fraction of the unit cube is contained in the sphere. In ten dimensions, less than 2% of the cube is filled by the sphere, so that typically more than 50 attempts will be needed. In seventy dimensions, less than [math]\displaystyle{ 10^{-24} }[/math] of the cube is filled, meaning typically a trillion quadrillion trials will be needed, far more than a computer could ever carry out.

Uniformly at random within the n-ball

With a point selected uniformly at random from the surface of the unit (n − 1)-sphere (e.g., by using Marsaglia's algorithm), one needs only a radius to obtain a point uniformly at random from within the unit n-ball. If u is a number generated uniformly at random from the interval [0, 1] and x is a point selected uniformly at random from the unit (n − 1)-sphere, then u^1/n x is uniformly distributed within the unit n-ball.

Alternatively, points may be sampled uniformly from within the unit n-ball by a reduction from the unit (n + 1)-sphere. In particular, if (x₁, x₂, ..., x_n+2) is a point selected uniformly from the unit (n + 1)-sphere, then (x₁, x₂, ..., x_n) is uniformly distributed within the unit n-ball (i.e., by simply discarding two coordinates).

If n is sufficiently large, most of the volume of the n-ball will be contained in the region very close to its surface, so a point selected from that volume will also probably be close to the surface. This is one of the phenomena leading to the so-called curse of dimensionality that arises in some numerical and other applications.

Distribution of the first coordinate

Let [math]\displaystyle{ y = x_1^2 }[/math] be the square of the first coordinate of a point sampled uniformly at random from the (n-1)-sphere, then its probability density function, for [math]\displaystyle{ y\in [0, 1] }[/math], is

[math]\displaystyle{ \rho(y) = \frac{\Gamma\bigl(\frac{n}{2} \bigr)}{\sqrt\pi \; \Gamma\bigl(\frac{n-1}{2}\bigr)} (1-y)^{(n-3)/2}y^{-1/2}. }[/math]

Let [math]\displaystyle{ z = y/N }[/math] be the appropriately scaled version, then at the [math]\displaystyle{ N\to \infty }[/math] limit, the probability density function of [math]\displaystyle{ z }[/math] converges to [math]\displaystyle{ (2\pi ze^z)^{-1/2} }[/math]. This is sometimes called the Porter–Thomas distribution.

Specific spheres

0-sphere

The pair of points {±R} with the discrete topology for some R > 0. The only sphere that is not path-connected. Parallelizable.

1-sphere

Commonly called a circle. Has a nontrivial fundamental group. Abelian Lie group structure U(1); the circle group. Homeomorphic to the real projective line.

2-sphere

Commonly simply called a sphere. For its complex structure, see Riemann sphere. Homeomorphic to the complex projective line

3-sphere

Parallelizable, principal U(1)-bundle over the 2-sphere, Lie group structure Sp(1).

4-sphere

Homeomorphic to the quaternionic projective line, HP¹. SO(5) / SO(4).

5-sphere

Principal U(1)-bundle over CP². SO(6) / SO(5) = SU(3) / SU(2). It is undecidable whether a given n-dimensional manifold is homeomorphic to Sⁿ for n ≥ 5.

6-sphere

Possesses an almost complex structure coming from the set of pure unit octonions. SO(7) / SO(6) = G₂ / SU(3). The question of whether it has a complex structure is known as the Hopf problem, after Heinz Hopf.

7-sphere

Topological quasigroup structure as the set of unit octonions. Principal Sp(1)-bundle over S⁴. Parallelizable. SO(8) / SO(7) = SU(4) / SU(3) = Sp(2) / Sp(1) = Spin(7) / G₂ = Spin(6) / SU(3). The 7-sphere is of particular interest since it was in this dimension that the first exotic spheres were discovered.

8-sphere

Homeomorphic to the octonionic projective line OP¹.

23-sphere

A highly dense sphere-packing is possible in 24-dimensional space, which is related to the unique qualities of the Leech lattice.

Octahedral sphere

The octahedral n-sphere is defined similarly to the n-sphere but using the 1-norm

[math]\displaystyle{ S^n = \left\{ x \in \mathbb{R}^{n+1} : \left\| x \right\|_1 = 1 \right\} }[/math]

In general, it takes the shape of a cross-polytope.

The octahedral 1-sphere is a square (without its interior). The octahedral 2-sphere is a regular octahedron; hence the name. The octahedral n-sphere is the topological join of n + 1 pairs of isolated points. Intuitively, the topological join of two pairs is generated by drawing a segment between each point in one pair and each point in the other pair; this yields a square. To join this with a third pair, draw a segment between each point on the square and each point in the third pair; this gives a octahedron.

See also

• Conformal geometry – Study of angle-preserving transformations of a geometric space
• Exotic sphere – Smooth manifold that is homeomorphic but not diffeomorphic to a sphere
• Homology sphere – Topological manifold whose homology coincides with that of a sphere
• Homotopy groups of spheres – How spheres of various dimensions can wrap around each other
• Inversive geometry
• Möbius transformation – Rational function of the form (az + b)/(cz + d)

References

• Marsaglia, G. (1972). "Choosing a Point from the Surface of a Sphere". Annals of Mathematical Statistics 43 (2): 645–646. doi:10.1214/aoms/1177692644. 
• Huber, Greg (1982). "Gamma function derivation of n-sphere volumes". Amer. Math. Monthly 89 (5): 301–302. doi:10.2307/2321716. 
• Weeks, Jeffrey R. (1985). The Shape of Space: how to visualize surfaces and three-dimensional manifolds. Marcel Dekker. ISBN 978-0-8247-7437-0(Chapter 14: The Hypersphere). 
• Kalnins, E. G.; Miller, W. (1986). "Separation of variables on n-dimensionsional Riemannian manifolds. I. the n-sphere S_n and Euclidean n-sparce R_n". J. Math. Phys. 27: 1721-1746. doi:10.1063/1.527088. 
• Flanders, Harley (1989). Differential forms with applications to the physical sciences. New York: Dover Publications. ISBN 978-0-486-66169-8. 
• Moura, Eduarda; Henderson, David G. (1996). Experiencing geometry: on plane and sphere. Prentice Hall. ISBN 978-0-13-373770-7. https://archive.org/details/experiencinggeom0000hend(Chapter 20: 3-spheres and hyperbolic 3-spaces). 
• Barnea, Nir (1999). "Hyperspherical functions with arbitrary permutational symmetry: Reverse construction". Phys. Rev. A 59 (2): 1135–1146. doi:10.1103/PhysRevA.59.1135. Bibcode: 1999PhRvA..59.1135B. 

External links

• Weisstein, Eric W.. "Hypersphere". http://mathworld.wolfram.com/Hypersphere.html.