Conic constant
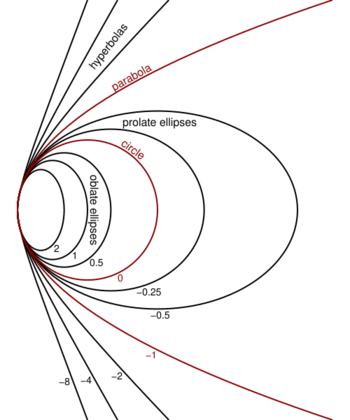
In geometry, the conic constant (or Schwarzschild constant,[1] after Karl Schwarzschild) is a quantity describing conic sections, and is represented by the letter K. The constant is given by where e is the eccentricity of the conic section.
The equation for a conic section with apex at the origin and tangent to the y axis is alternately where R is the radius of curvature at x = 0.
This formulation is used in geometric optics to specify oblate elliptical (K > 0), spherical (K = 0), prolate elliptical (0 > K > −1), parabolic (K = −1), and hyperbolic (K < −1) lens and mirror surfaces. When the paraxial approximation is valid, the optical surface can be treated as a spherical surface with the same radius.
Some[which?] non-optical design references use the letter p as the conic constant. In these cases, p = K + 1.
References
- ↑ Rakich, Andrew (2005-08-18). Sasian, Jose M; Koshel, R. John; Juergens, Richard C. eds. "The 100th birthday of the conic constant and Schwarzschild's revolutionary papers in optics". Novel Optical Systems Design and Optimization VIII (International Society for Optics and Photonics) 5875: 587501. doi:10.1117/12.635041. Bibcode: 2005SPIE.5875....1R. https://www.spiedigitallibrary.org/conference-proceedings-of-spie/5875/587501/The-100th-birthday-of-the-conic-constant-and-Schwarzschilds-revolutionary/10.1117/12.635041.short.
- Smith, Warren J. (2008). Modern Optical Engineering, 4th ed. McGraw-Hill Professional. pp. 512–515. ISBN 978-0-07-147687-4.
 |
