Cop-win graph

From HandWiki
Short description: Type of graph related to pursuit–evasion

In graph theory, a cop-win graph is an undirected graph on which the pursuer (cop) can always win a pursuit–evasion game against a robber, with the players taking alternating turns in which they can choose to move along an edge of a graph or stay put, until the cop lands on the robber's vertex.[1] Finite cop-win graphs are also called dismantlable graphs or constructible graphs, because they can be dismantled by repeatedly removing a dominated vertex (one whose closed neighborhood is a subset of another vertex's neighborhood) or constructed by repeatedly adding such a vertex. The cop-win graphs can be recognized in polynomial time by a greedy algorithm that constructs a dismantling order. They include the chordal graphs, and the graphs that contain a universal vertex.

Definitions

Pursuit–evasion

Cop-win graphs can be defined by a pursuit–evasion game in which two players, a cop and a robber, are positioned at different initial vertices of a given undirected graph. The cop chooses an initial vertex first, and then the robber chooses. Next, they play in turns, again with the cop first. On each player's turn, the player may either move to an adjacent vertex or stay put. The game ends, and the cop wins, if the cop can end a turn on the same vertex as the robber. The robber wins by indefinitely evading the cop. A cop-win graph is a graph with the property that, when the players choose starting positions and then move in this way, the cop can always force a win. If an undirected graph is not a cop-win graph, it is called a robber-win graph.[2]

Dismantling

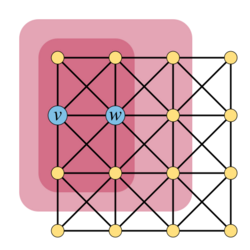
In this graph, vertex v is dominated by vertex w: the closed neighborhood of v, N[v] (inner shaded region) is a subset of the closed neighborhood of w, N[w] (outer shaded region)

The closed neighborhood N[v] of a vertex v in a given graph is the set of vertices consisting of v itself and all other vertices adjacent to v. The vertex v is said to be dominated by another vertex w when N[v] ⊂ N[w]. That is, v and w are adjacent, and every other neighbor of v is also a neighbor of w.[3] (Nowakowski Winkler) call a vertex that is dominated by another vertex an irreducible vertex.[2]

A dismantling order or domination elimination ordering of a given graph is an ordering of the vertices such that, if the vertices are removed one-by-one in this order, each vertex (except the last) is dominated at the time it is removed. A graph is dismantlable if and only if it has a dismantling order.[2][3]

Equivalence of cop-win and dismantlability

Every finite dismantlable graph is cop-win. This can be proved by mathematical induction, with a one-vertex graph (trivially won by the cop) as a base case. For a larger graph, let v be any dominated vertex. By the induction hypothesis, the cop has a winning strategy on the graph formed by removing v, and can follow the same strategy on the original graph by pretending that the robber is on the vertex that dominates v whenever the robber is actually on v. Following this strategy will result either in an actual win of the game, or in a position where the robber is on v and the cop is on the dominating vertex, from which the cop can win in one more move.[2][4] A cop following this inductive strategy on a graph with n vertices takes at most n moves to win, regardless of starting position. By choosing the cop's starting position carefully, one can use the same idea to prove that, in an n-vertex graph, the cop can force a win in at most n − 4 moves.[5][6][7]

Conversely, every cop-win graph has a dominated vertex. For, in a graph with no dominated vertices, if the robber has not already lost, then there is a safe move to a position not adjacent to the cop, and the robber can continue the game indefinitely by playing one of these safe moves at each turn.[2][8] Additionally, if v is a dominated vertex in a cop-win graph, then removing v must produce another cop-win graph, for otherwise the robber could play within that subgraph, pretending that the cop is on the vertex that dominates v whenever the cop is actually on v, and never get caught. It follows by induction from these two principles that every finite cop-win graph is dismantlable.[2][9]

Closure properties

Script error: No such module "Chessboard". A family of mathematical objects is said to be closed under a set of operations if combining members of the family always produces another member of that family. In that sense, the family of cop-win graphs is closed under strong products of graphs. Each vertex in the strong product corresponds to a pair of vertices in each of two factor graphs. The cop can win in a strong product of two cop-win graphs by, first, playing to win in one of these two factor graphs, reaching a pair whose first component is the same as the robber. Then, while staying in pairs whose first component is the same as the robber, the cop can play to win in the second of the two factors.[2][10] For instance, the king's graph, a strong product of two path graphs, is cop-win. On this graph, the vertices correspond to the squares of a chessboard, and both the cop and robber move like a king in the game of chess, to a square that is adjacent horizontally, vertically, or diagonally. The product-based strategy for the cop would be to first move to the same row as the robber, and then move towards the column of the robber while in each step remaining on the same row as the robber.[11]

It is not true that every induced subgraph of a cop-win graph is cop-win. However, certain special induced subgraphs do remain cop-win. (Nowakowski Winkler) define a retraction of a graph G onto one of its induced subgraphs H to be a mapping from the vertices of G to the vertices of H that maps each vertex of H to itself, and that maps each pair of adjacent vertices of G either to the same vertex as each other or to a pair of adjacent vertices in H. Then the family of cop-win graphs is closed under retraction. This is because a cop can win in H by simulating a game in G. Whenever the winning strategy in G would call for the cop to stay put, or to follow an edge whose endpoints are mapped to the same vertex of H, the cop stays put in H. And in all other cases, the cop follows the edge in H that is the image under the retraction of a winning edge in G.[2]

Recognition algorithms

Several different strategies are known for checking whether a graph is cop-win, and if so finding a dismantling sequence allowing the cop to win in the graph. These include greedy algorithms, and a more complicated algorithm based on counting shared neighbors of vertices.

Greedy algorithm

A dismantling order can be found by a simple greedy algorithm that repeatedly finds and removes any dominated vertex. The process succeeds, by reducing the graph to a single vertex, if and only if the graph is cop-win. Therefore, as well as providing an algorithm for finding dismantling orders, this method provides an algorithm for testing whether a given graph is cop-win. One way for this algorithm to find the dominated vertices that it removes is to perform the following steps:

  • Find all triangles in the graph, and count the number of triangles that each edge participates in.
  • Repeatedly find a vertex v that is an endpoint of an edge participating in a number of triangles equal to the degree of v minus one, delete v, and decrement the triangles per edge of each remaining edge that formed a triangle with v.

In a graph with n vertices, m edges, and degeneracy d, this process can be carried out in time O(dm).[12]

Counting neighbors

An alternative and more complicated algorithm by (Spinrad 2004) involves maintaining a number called the deficit for each adjacent pair of vertices (x, y), which counts the number of neighbors of x that are not neighbors of y. If this number becomes zero, after other vertices have been removed, then x is dominated by y and may also be removed. It constructs and maintains the actual deficit set (neighbors of x that are not neighbors of y) only for pairs (x, y) for which the deficit is small.[13]

To speed up its computations, Spinrad's algorithm uses a subroutine for counting neighbors among small blocks of log2 n vertices. If B is a set of vertices that the algorithm has selected to be a block, then for any other vertex, the set of neighbors of that vertex in B can be represented as a binary number with log2 n bits. These numbers allow the algorithm to count, for any two vertices x and y, how much B contributes to the deficit of x and y, in constant time, by a combination of bitwise operations and table lookups. Using this subroutine, the algorithm performs the following steps:

  • Create blocks from an arbitrary partition of the vertices, and find the numbers representing the neighbors of each vertex in each block.
  • Use the block-counting subroutine to compute the deficit for all adjacent pairs of vertices.
  • Repeat the following steps until all vertices have been removed:
    • Construct the deficit set for all adjacent pairs that have deficit at most log n and that have not already had this set constructed. The initial system of blocks can be used to speed up this construction.
    • Repeat the following steps log n times:
      • Find a pair (x, y) with constructed but empty deficit set. If no such pair exists, the graph is not cop-win; in this case, abort the algorithm.
      • Delete vertex x
      • Remove x from all constructed deficit sets that it belongs to.
    • Construct a block of the log n removed vertices and numbers representing all other vertices' adjacencies within this block.
    • Use the block-counting subroutine, on this one block, to update the deficits for all edges.

Spinrad states the total time for this algorithm as O(n3/log n).[13]

In infinite graphs

The computability of algorithmic problems involving cop-win graphs has also been studied for infinite graphs. In the case of infinite graphs, it is possible to construct computable countably infinite graphs, on which an omniscient robber could always evade any cop, but for which no algorithm can follow this strategy. These graphs can even be infinite trees, with a finite number of edges per vertex. By Kőnig's lemma, such a tree must have an infinite path, and an omniscient robber can win by walking away from the cop along this path, but the path cannot be found by an algorithm. Instead, every algorithm for choosing moves for the robber can be beaten by a cop who simply walks in the tree along the unique path towards the robber. Analogously, it is possible to construct computable countably infinite cop-win graphs, on which an omniscient cop has a winning strategy that always terminates in a finite number of moves, but for which no algorithm can follow this strategy. On such graphs, every algorithm for choosing moves for the cop can be evaded indefinitely by the robber.[14]

Related families of graphs

In this graph, u is a universal vertex: it is adjacent to all other vertices

Every finite chordal graph is a dismantlable graph, and every elimination ordering of a chordal graph (an ordering of the vertices in which the later neighbors of each vertex form a clique) is a valid dismantling order. However, there exist infinite chordal graphs, and even infinite chordal graphs of diameter two, that are not cop-win.[15][16] For other types of graphs, there may exist infinite cop-win graphs of that type even when there are no finite ones; for instance, this is true for the vertex-transitive graphs that are not complete graphs.[17]

A universal vertex in a graph is a vertex u that is adjacent to all other vertices. Whenever a graph has a universal vertex, it is dismantlable, because every other vertex is dominated by the universal vertex, and any vertex ordering that places the universal vertex last is a valid dismantling order. Conversely, almost all dismantlable graphs have a universal vertex, in the sense that, among all n-vertex dismantlable graphs, the fraction of these graphs that have a universal vertex goes to one in the limit as n goes to infinity.[18]

The visibility graphs of simple polygons are always cop-win. These are graphs defined from the vertices of a polygon, with an edge whenever two vertices can be connected by a line segment that does not pass outside the polygon. (In particular, vertices that are adjacent in the polygon are also adjacent in the graph.) Even when the cop and robber are allowed to move on straight line segments within the polygon, rather than vertex-to-vertex, the cop can win by always moving on the first step of a shortest path to the robber. Such a move cuts off part of the polygon which the robber can never double back to reach. When the cop starts at a vertex and the robber is restricted to moves between vertices, this strategy also limits the cop to vertices, so it is a valid winning strategy for the visibility graph.[19]

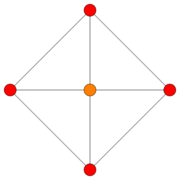
The five-vertex wheel graph is cop-win but not hereditarily cop-win.

The hereditarily cop-win graphs are the graphs in which every isometric subgraph (a subgraph [math]\displaystyle{ H \subseteq G }[/math] such that for any two vertices in [math]\displaystyle{ H }[/math] the distance between them measured in [math]\displaystyle{ G }[/math] is the same as the distance between them measured in [math]\displaystyle{ H }[/math]) is cop-win. This is not true for all cop-win graphs; for instance, the five-vertex wheel graph is cop-win but contains an isometric 4-cycle, which is not cop-win, so this wheel graph is not hereditarily cop-win. The hereditarily cop-win graphs are the same as the bridged graphs, graphs in which every cycle of length four or more has a shortcut, a pair of vertices closer in the graph than they are in the cycle.[20] A cop-win graph is hereditarily cop-win if and only if it has neither the 4-cycle nor 5-cycle as induced cycles. For a hereditarily cop-win graph, the reversal of any breadth-first traversal is a valid dismantling order, from which it follows that any vertex can be chosen as the last vertex of a dismantling order.[21]

A similar game with larger numbers of cops can be used to define the cop number of a graph, the smallest number of cops needed to win the game. The cop-win graphs are exactly the graphs of cop number equal to one.[22] Bonato and Nowakowski describe this game intuitively as the number of ghosts that would be needed to force a Pac-Man player to lose, using the given graph as the field of play.[23] The game used to define cop number should be distinguished from a different cops-and-robbers game used in one definition of treewidth, which allows the cops to move to arbitrary vertices rather than requiring them to travel along graph edges.[24]

History

The game with a single cop, and the cop-win graphs defined from it, were introduced by (Quilliot 1978).[25][26] Another early reference is the work of (Nowakowski Winkler), who were introduced to the game by G. Gabor.[2][26] The game with multiple cops, and the cop number defined from it, were first studied by (Aigner Fromme).[22][26]

References

  1. ↑ Bonato, Anthony; Nowakowski, Richard J. (2011), The Game of Cops and Robbers on Graphs, Student Mathematical Library, 61, Providence, RI: American Mathematical Society, doi:10.1090/stml/061, ISBN 978-0-8218-5347-4 
  2. ↑ 2.0 2.1 2.2 2.3 2.4 2.5 2.6 2.7 2.8 Nowakowski, Richard (1983), "Vertex-to-vertex pursuit in a graph", Discrete Mathematics 43 (2–3): 235–239, doi:10.1016/0012-365X(83)90160-7 
  3. ↑ 3.0 3.1 Chepoi, Victor (1998), "On distance-preserving and domination elimination orderings", SIAM Journal on Discrete Mathematics 11 (3): 414–436, doi:10.1137/S0895480195291230 
  4. ↑ Bonato & Nowakowski (2011), Theorem 2.3, page 32.
  5. ↑ Bonato, A.; Golovach, P.; Hahn, G. (2009), "The capture time of a graph", Discrete Mathematics 309 (18): 5588–5595, doi:10.1016/j.disc.2008.04.004 
  6. ↑ Gavenčiak, Tomáš (2010), "Cop-win graphs with maximum capture-time", Discrete Mathematics 310 (10–11): 1557–1563, doi:10.1016/j.disc.2010.01.015 
  7. ↑ Bonato & Nowakowski (2011), p. 36.
  8. ↑ Bonato & Nowakowski (2011), Lemma 2.1, page 31.
  9. ↑ Bonato & Nowakowski (2011), Theorem 2.2, page 32.
  10. ↑ Bonato & Nowakowski (2011), Theorem 2.8, page 43.
  11. ↑ For the fact that a strong product of paths is cop-win, see (Nowakowski Winkler). For the fact that the king's graph is a strong product of paths, see Berend, Daniel; Korach, Ephraim; Zucker, Shira (2005), "Two-anticoloring of planar and related graphs", 2005 International Conference on Analysis of Algorithms, Discrete Mathematics & Theoretical Computer Science Proceedings, Nancy: Association for Discrete Mathematics & Theoretical Computer Science, pp. 335–341, http://www.emis.de/journals/DMTCS/pdfpapers/dmAD0130.pdf 
  12. ↑ Lin, Min Chih; Soulignac, Francisco J.; Szwarcfiter, Jayme L. (2012), "Arboricity, h-index, and dynamic algorithms", Theoretical Computer Science 426–427: 75–90, doi:10.1016/j.tcs.2011.12.006 
  13. ↑ 13.0 13.1 Spinrad, Jeremy P. (2004), "Recognizing quasi-triangulated graphs", Discrete Applied Mathematics 138 (1–2): 203–213, doi:10.1016/S0166-218X(03)00295-6 
  14. ↑ Stahl, Rachel D. (September 2021), "Computability and the game of cops and robbers on graphs", Archive for Mathematical Logic 61 (3–4): 373–397, doi:10.1007/s00153-021-00794-3 
  15. ↑ Hahn, Geňa; Laviolette, François; Sauer, Norbert; Woodrow, Robert E. (2002), "On cop-win graphs", Discrete Mathematics 258 (1–3): 27–41, doi:10.1016/S0012-365X(02)00260-1 
  16. ↑ Bonato & Nowakowski (2011), Section 7.4, Infinite chordal graphs, pp. 178–182.
  17. ↑ Bonato & Nowakowski (2011), Section 7.5, Vertex-transitive cop-win graphs, pp. 182–187.
  18. ↑ Bonato, Anthony; Kemkes, Graeme; Prałat, Paweł (2012), "Almost all cop-win graphs contain a universal vertex", Discrete Mathematics 312 (10): 1652–1657, doi:10.1016/j.disc.2012.02.018 
  19. ↑ "Visibility graphs, dismantlability, and the cops and robbers game", Computational Geometry 66: 14–27, 2017, doi:10.1016/j.comgeo.2017.07.001 
  20. ↑ Anstee, R. P.; Farber, M. (1988), "On bridged graphs and cop-win graphs", Journal of Combinatorial Theory, Series B 44 (1): 22–28, doi:10.1016/0095-8956(88)90093-7 
  21. ↑ Chepoi, Victor (1997), "Bridged graphs are cop-win graphs: an algorithmic proof", Journal of Combinatorial Theory, Series B 69 (1): 97–100, doi:10.1006/jctb.1996.1726 
  22. ↑ 22.0 22.1 Aigner, M.; Fromme, M. (1984), "A game of cops and robbers", Discrete Applied Mathematics 8 (1): 1–11, doi:10.1016/0166-218X(84)90073-8 
  23. ↑ Bonato & Nowakowski (2011), pp. 1–3.
  24. ↑ "Graph searching and a min-max theorem for tree-width", Journal of Combinatorial Theory, Series B 58 (1): 22–33, 1993, doi:10.1006/jctb.1993.1027 
  25. ↑ Quilliot, Alain (1978) (in fr), Jeux et pointes fixes sur les graphes, Thèse de 3ème cycle, Pierre and Marie Curie University, pp. 131–145 , as cited by (Bonato Nowakowski)
  26. ↑ 26.0 26.1 26.2 Bonato & Nowakowski (2011), p. 4.

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Cop-win_graph&oldid=3016534"