Dini's surface

Dini's surface plotted with adjustable parameters by Wolfram Mathematica program

Dini's Surface with constants a = 1, b = 0.5 and 0 ≤ u ≤ 4π and 0<v<1.

In geometry, Dini's surface is a surface with constant negative curvature that can be created by twisting a pseudosphere. It is named after Ulisse Dini and described by the following parametric equations:

[math]\displaystyle{ \begin{align} x&=a \cos u \sin v \\ y&=a \sin u \sin v \\ z&=a \left(\cos v +\ln \tan \frac{v}{2} \right) + bu \end{align} }[/math]

Dini's surface with 0 ≤ u ≤ 4π and 0.01 ≤ v ≤ 1 and constants a = 1.0 and b = 0.2.

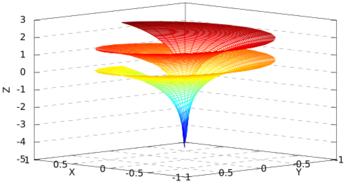
Another description is a generalized helicoid constructed from the tractrix.

See also

• Dini derivative
• Dini test
• Dini's theorem
• List of surfaces