Displaced Poisson distribution

Displaced Poisson Distribution

Probability mass function 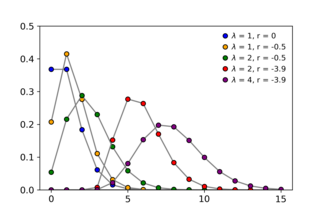Displaced Poisson distributions for several values of $\lambda$ and $r$. At $r=0$, the Poisson distribution is recovered. The probability mass function is only defined at integer values.
Parameters	$\lambda \in (0,\mathrm{\infty })$, $r\in (-\mathrm{\infty },\mathrm{\infty })$
Support	$k\in {\mathbb{\mathbb{N}}}_0$
Mean	$\lambda -r$
Mode	$\{\begin{array}{ll}\lceil \lambda -r\rceil -1,\lfloor \lambda -r\rfloor & \text{if }\lambda \ge r+1\\ 0& \text{if }\lambda <r+1\\ \end{array}$
Variance	$\lambda$
MGF	$e^{\lambda \left(e^{t-1}\right)-tr}\cdot \frac{I(r+s,\lambda e^t)}{I(r+s,\lambda )}$,  $I(r,\lambda )=\sum _{y=r}^{\mathrm{\infty }}\frac{e^{-\lambda }{\lambda }^y}{y!}$ When $r$ is a negative integer, this becomes $e^{\lambda \left(e^{t-1}\right)-tr}$

In statistics, the displaced Poisson, also known as the hyper-Poisson distribution, is a generalization of the Poisson distribution.

Definitions

Probability mass function

The probability mass function is

$P(X=n)=\{\begin{array}{ll}{e}^{-\lambda }\frac{{\lambda }^{n+r}}{(n+r)!}\cdot \frac{1}{I(r,\lambda )},n=0,1,2,\dots & \text{if }r\ge 0\\ e^{-\lambda }\frac{{\lambda }^{n+r}}{(n+r)!}\cdot \frac{1}{I(r+s,\lambda )},n=s,s+1,s+2,\dots & \text{otherwise}\end{array}$

where $\lambda >0$ and r is a new parameter; the Poisson distribution is recovered at r = 0. Here $I(r,\lambda )$ is the Pearson's incomplete gamma function:

$I(r,\lambda )=\sum _{y=r}^{\mathrm{\infty }}\frac{e^{-\lambda }{\lambda }^y}{y!},$

where s is the integral part of r. The motivation given by Staff is that the ratio of successive probabilities in the Poisson distribution (that is $P(X=n)/P(X=n-1)$) is given by $\lambda /n$ for $n>0$ and the displaced Poisson generalizes this ratio to $\lambda /(n+r)$.

Examples

One of the limitations of the Poisson distribution is that it assumes equidispersion – the mean and variance of the variable are equal. The displaced Poisson distribution may be useful to model underdispersed or overdispersed data, such as:

• the distribution of insect populations in crop fields;
• the number of flowers on plants;
• motor vehicle crash counts; and
• word or sentence lengths in writing.

Properties

Descriptive Statistics

• For a displaced Poisson-distributed random variable, the mean is equal to $\lambda -r$ and the variance is equal to $\lambda$.
• The mode of a displaced Poisson-distributed random variable are the integer values bounded by $\lambda -r-1$ and $\lambda -r$ when $\lambda \ge r+1$. When $\lambda <r+1$, there is a single mode at $x=0$.
• The first cumulant ${\kappa }_1$ is equal to $\lambda -r$ and all subsequent cumulants ${\kappa }_n,n\ge 2$ are equal to $\lambda$.