Dissipative soliton

From HandWiki

Dissipative solitons (DSs) are stable solitary localized structures that arise in nonlinear spatially extended dissipative systems due to mechanisms of self-organization. They can be considered as an extension of the classical soliton concept in conservative systems. An alternative terminology includes autosolitons, spots and pulses. Apart from aspects similar to the behavior of classical particles like the formation of bound states, DSs exhibit interesting behavior – e.g. scattering, creation and annihilation – all without the constraints of energy or momentum conservation. The excitation of internal degrees of freedom may result in a dynamically stabilized intrinsic speed, or periodic oscillations of the shape.

Historical development

Origin of the soliton concept

DSs have been experimentally observed for a long time. Helmholtz[1] measured the propagation velocity of nerve pulses in 1850. In 1902, Lehmann[2] found the formation of localized anode spots in long gas-discharge tubes. Nevertheless, the term "soliton" was originally developed in a different context. The starting point was the experimental detection of "solitary water waves" by Russell in 1834.[3] These observations initiated the theoretical work of Rayleigh[4] and Boussinesq[5] around 1870, which finally led to the approximate description of such waves by Korteweg and de Vries in 1895; that description is known today as the (conservative) KdV equation.[6]

On this background the term "soliton" was coined by Zabusky and Kruskal[7] in 1965. These authors investigated certain well localised solitary solutions of the KdV equation and named these objects solitons. Among other things they demonstrated that in 1-dimensional space solitons exist, e.g. in the form of two unidirectionally propagating pulses with different size and speed and exhibiting the remarkable property that number, shape and size are the same before and after collision.

Gardner et al.[8] introduced the inverse scattering technique for solving the KdV equation and proved that this equation is completely integrable. In 1972 Zakharov and Shabat[9] found another integrable equation and finally it turned out that the inverse scattering technique can be applied successfully to a whole class of equations (e.g. the nonlinear Schrödinger and sine-Gordon equations). From 1965 up to about 1975, a common agreement was reached: to reserve the term soliton to pulse-like solitary solutions of conservative nonlinear partial differential equations that can be solved by using the inverse scattering technique.

Weakly and strongly dissipative systems

With increasing knowledge of classical solitons, possible technical applicability came into perspective, with the most promising one at present being the transmission of optical solitons via glass fibers for the purpose of data transmission. In contrast to conservative systems, solitons in fibers dissipate energy and this cannot be neglected on an intermediate and long time scale. Nevertheless, the concept of a classical soliton can still be used in the sense that on a short time scale dissipation of energy can be neglected. On an intermediate time scale one has to take small energy losses into account as a perturbation, and on a long scale the amplitude of the soliton will decay and finally vanish.[10]

There are however various types of systems which are capable of producing solitary structures and in which dissipation plays an essential role for their formation and stabilization. Although research on certain types of these DSs has been carried out for a long time (for example, see the research on nerve pulses culminating in the work of Hodgkin and Huxley[11] in 1952), since 1990 the amount of research has significantly increased (see e.g.[12][13][14][15]) Possible reasons are improved experimental devices and analytical techniques, as well as the availability of more powerful computers for numerical computations. Nowadays, it is common to use the term dissipative solitons for solitary structures in strongly dissipative systems.

Experimental observations

Today, DSs can be found in many different experimental set-ups. Examples include

  • Gas-discharge systems: plasmas confined in a discharge space which often has a lateral extension large compared to the main discharge length. DSs arise as current filaments between the electrodes and were found in DC systems with a high-ohmic barrier,[16] AC systems with a dielectric barrier,[17] and as anode spots,[18] as well as in an obstructed discharge with metallic electrodes.[19]
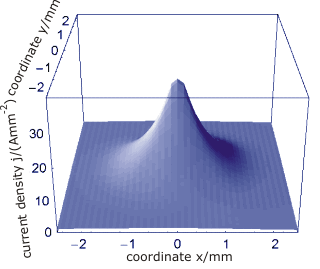
  • DSs experimentally observed in planar dc gas-discharge systems with high-ohmic barrier

  • Averaged current density distribution without oscillatory tails.

  • Averaged current density distribution with oscillatory tails.

  • Semiconductor systems: these are similar to gas-discharges; however, instead of a gas, semiconductor material is sandwiched between two planar or spherical electrodes. Set-ups include Si and GaAs pin diodes,[20] n-GaAs,[21] and Si p+−n+−p−n−,[22] and ZnS:Mn structures.[23]
  • Nonlinear optical systems: a light beam of high intensity interacts with a nonlinear medium. Typically the medium reacts on rather slow time scales compared to the beam propagation time. Often, the output is fed back into the input system via single-mirror feedback or a feedback loop. DSs may arise as bright spots in a two-dimensional plane orthogonal to the beam propagation direction; one may, however, also exploit other effects like polarization. DSs have been observed for saturable absorbers,[24] degenerate optical parametric oscillators (DOPOs),[25] liquid crystal light valves (LCLVs),[26] alkali vapor systems,[27] photorefractive media,[28] and semiconductor microresonators.[29]
  • If the vectorial properties of DSs are considered, vector dissipative soliton could also be observed in a fiber laser passively mode locked through saturable absorber,[30]
  • In addition, multiwavelength dissipative soliton in an all normal dispersion fiber laser passively mode-locked with a SESAM has been obtained. It is confirmed that depending on the cavity birefringence, stable single-, dual- and triple-wavelength dissipative soliton can be formed in the laser. Its generation mechanism can be traced back to the nature of dissipative soliton.[31]
  • Chemical systems: realized either as one- and two-dimensional reactors or via catalytic surfaces, DSs appear as pulses (often as propagating pulses) of increased concentration or temperature. Typical reactions are the Belousov–Zhabotinsky reaction,[32] the ferrocyanide-iodate-sulphite reaction as well as the oxidation of hydrogen,[33] CO,[34] or iron.[35] Nerve pulses[11] or migraine aura waves[36] also belong to this class of systems.
  • Vibrated media: vertically shaken granular media,[37] colloidal suspensions,[38] and Newtonian fluids[39] produce harmonically or sub-harmonically oscillating heaps of material, which are usually called oscillons.
  • Hydrodynamic systems: the most prominent realization of DSs are domains of convection rolls on a conducting background state in binary liquids.[40] Another example is a film dragging in a rotating cylindric pipe filled with oil.[41]
  • Electrical networks: large one- or two-dimensional arrays of coupled cells with a nonlinear current–voltage characteristic.[42] DSs are characterized by a locally increased current through the cells.

Remarkably enough, phenomenologically the dynamics of the DSs in many of the above systems are similar in spite of the microscopic differences. Typical observations are (intrinsic) propagation, scattering, formation of bound states and clusters, drift in gradients, interpenetration, generation, and annihilation, as well as higher instabilities.

Theoretical description

Most systems showing DSs are described by nonlinear partial differential equations. Discrete difference equations and cellular automata are also used. Up to now, modeling from first principles followed by a quantitative comparison of experiment and theory has been performed only rarely and sometimes also poses severe problems because of large discrepancies between microscopic and macroscopic time and space scales. Often simplified prototype models are investigated which reflect the essential physical processes in a larger class of experimental systems. Among these are

  • Reaction–diffusion systems, used for chemical systems, gas-discharges and semiconductors.[43] The evolution of the state vector q(x, t) describing the concentration of the different reactants is determined by diffusion as well as local reactions:
[math]\displaystyle{ \partial_t \boldsymbol{q} = \underline{\boldsymbol{D}} \, \Delta \boldsymbol{q} + \boldsymbol{R}(\boldsymbol{q}). }[/math]
A frequently encountered example is the two-component Fitzhugh–Nagumo-type activator–inhibitor system
[math]\displaystyle{ \left( \begin{array}{c} \tau_u \, \partial_t u\\ \tau_v \, \partial_t v \end{array} \right) = \left(\begin{array}{cc} d_u^2 &0\\ 0 & d_v^2 \end{array}\right) \left( \begin{array}{c} \Delta u \\ \Delta v \end{array} \right) + \left(\begin{array}{c} \lambda u -u^3 - \kappa_3 v +\kappa_1\\u-v \end{array}\right). }[/math]
Stationary DSs are generated by production of material in the center of the DSs, diffusive transport into the tails and depletion of material in the tails. A propagating pulse arises from production in the leading and depletion in the trailing end.[44] Among other effects, one finds periodic oscillations of DSs ("breathing"),[45][46] bound states,[47] and collisions, merging, generation and annihilation.[48]
  • Ginzburg–Landau type systems for a complex scalar q(x, t) used to describe nonlinear optical systems, plasmas, Bose-Einstein condensation, liquid crystals and granular media.[49] A frequently found example is the cubic-quintic subcritical Ginzburg–Landau equation
[math]\displaystyle{ \partial_t q = (d_r+ i d_i) \, \Delta q + \ell_r q + (c_r + i c_i) |q|^2 q + (q_r + i q_i) |q|^4 q. }[/math]
To understand the mechanisms leading to the formation of DSs, one may consider the energy ρ = |q|2 for which one may derive the continuity equation
[math]\displaystyle{ \begin{align} & \partial_t \rho + \nabla \cdot \boldsymbol{m} = S = d_r(q \, \Delta q^\ast + q^\ast \, \Delta q) + 2 \ell_r \rho + 2 c_r \rho^2 + 2 q_r \rho^3 \\ & \text{with } \boldsymbol{m} = 2 d_i \operatorname{Im}(q^\ast \nabla q). \end{align} }[/math]
One can thereby show that energy is generally produced in the flanks of the DSs and transported to the center and potentially to the tails where it is depleted. Dynamical phenomena include propagating DSs in 1d,[50] propagating clusters in 2d,[51] bound states and vortex solitons,[52] as well as "exploding DSs".[53]
  • The Swift–Hohenberg equation is used in nonlinear optics and in the granular media dynamics of flames or electroconvection. Swift–Hohenberg can be considered as an extension of the Ginzburg–Landau equation. It can be written as
[math]\displaystyle{ \partial_t q = (s_r+ i s_i) \,\Delta^2 q + (d_r+ i d_i) \,\Delta q + \ell_r q + (c_r + i c_i)|q|^2 q + (q_r + i q_i) |q|^4 q. }[/math]
For dr > 0 one essentially has the same mechanisms as in the Ginzburg–Landau equation.[54] For dr < 0, in the real Swift–Hohenberg equation one finds bistability between homogeneous states and Turing patterns. DSs are stationary localized Turing domains on the homogeneous background.[55] This also holds for the complex Swift–Hohenberg equations; however, propagating DSs as well as interaction phenomena are also possible, and observations include merging and interpenetration.[56]
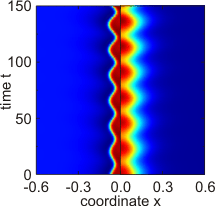
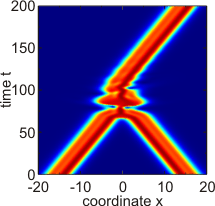
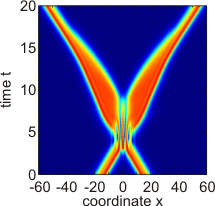
  • Space-time plots showing the dynamics and interaction of DSs as numerical solutions of the above model equations in one spatial dimension

  • Single "breathing" DS as solution of the two-component reaction-diffusion system with activator u (left half) and inhibitor v (right half).

  • DS collision ginzburg landau.gif
  • DS interpenetration swift hohenberg.gif

Particle properties and universality

DSs in many different systems show universal particle-like properties. To understand and describe the latter, one may try to derive "particle equations" for slowly varying order parameters like position, velocity or amplitude of the DSs by adiabatically eliminating all fast variables in the field description. This technique is known from linear systems, however mathematical problems arise from the nonlinear models due to a coupling of fast and slow modes.[57]

Similar to low-dimensional dynamic systems, for supercritical bifurcations of stationary DSs one finds characteristic normal forms essentially depending on the symmetries of the system. E.g., for a transition from a symmetric stationary to an intrinsically propagating DS one finds the Pitchfork normal form

[math]\displaystyle{ \dot{\boldsymbol{v}} = (\sigma - \sigma_0) \boldsymbol{v} - |\boldsymbol{v}|^2 \boldsymbol{v} }[/math]

for the velocity v of the DS,[58] here σ represents the bifurcation parameter and σ0 the bifurcation point. For a bifurcation to a "breathing" DS, one finds the Hopf normal form

[math]\displaystyle{ \dot{A} = (\sigma - \sigma_0) A - |A|^2 A }[/math]

for the amplitude A of the oscillation.[46] It is also possible to treat "weak interaction" as long as the overlap of the DSs is not too large.[59] In this way, a comparison between experiment and theory is facilitated.[60][61] Note that the above problems do not arise for classical solitons as inverse scattering theory yields complete analytical solutions.

See also

References

Inline

  1. ↑ Helmholtz, H. (1850). "Messungen über den zeitlichen Verlauf der Zuckung animalischer Muskeln und die Fortpflanzungsgeschwindigkeit der Reizung in den Nerven" (in de). Archiv für Anatomie, Physiologie und Wissenschaftliche Medicin 57: 276. https://www.biodiversitylibrary.org/item/110656#page/360/mode/1up. 
  2. ↑ Lehmann, O. (1902). "Gasentladungen in weiten Gefässen" (in de). Annalen der Physik (Wiley) 312 (1): 1–28. doi:10.1002/andp.19013120102. ISSN 0003-3804. https://gallica.bnf.fr/ark:/12148/bpt6k15317x/f9.image. 
  3. ↑ J. S. Russell, Report of the fourteenth meeting of the British Association for the Advancement of Science (1845): 311
  4. ↑ Rayleigh, J. W. (1876). "XXXII. On waves". The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science (Informa UK Limited) 1 (4): 257–279. doi:10.1080/14786447608639037. ISSN 1941-5982. 
  5. ↑ Boussinesq, J. (1871). "Hydrodynamique - Théorie de l'inlumescence liquide appelée onde solitaire ou de translation, se propageant dans un canal rectangulaire" (in fr). Comptes rendus hebdomadaires des séances de l'Académie des sciences 72: 755. https://gallica.bnf.fr/ark:/12148/bpt6k3029x/f759.item. 
  6. ↑ Korteweg, D. J.; de Vries, G. (1895). "XLI. On the change of form of long waves advancing in a rectangular canal, and on a new type of long stationary waves". The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science (Informa UK Limited) 39 (240): 422–443. doi:10.1080/14786449508620739. ISSN 1941-5982. https://zenodo.org/record/1431215. 
  7. ↑ Zabusky, N. J.; Kruskal, M. D. (9 August 1965). "Interaction of "Solitons" in a Collisionless Plasma and the Recurrence of Initial States". Physical Review Letters (American Physical Society) 15 (6): 240–243. doi:10.1103/physrevlett.15.240. ISSN 0031-9007. Bibcode: 1965PhRvL..15..240Z. 
  8. ↑ Gardner, Clifford S.; Greene, John M.; Kruskal, Martin D.; Miura, Robert M. (6 November 1967). "Method for Solving the Korteweg-deVries Equation". Physical Review Letters (American Physical Society) 19 (19): 1095–1097. doi:10.1103/physrevlett.19.1095. ISSN 0031-9007. Bibcode: 1967PhRvL..19.1095G. 
  9. ↑ Zakharov, V. E.; Shabat, A. B. (1975). "A scheme for integrating the nonlinear equations of mathematical physics by the method of the inverse scattering problem. I". Functional Analysis and Its Applications (Springer Science and Business Media) 8 (3): 226–235. doi:10.1007/bf01075696. ISSN 0016-2663. 
  10. ↑ Kivshar, Y. S.; Agrawal, G. P. (2003). Optical solitons : from fibers to photonic crystals. Amsterdam Boston: Academic Press. ISBN 978-0-12-410590-4. OCLC 162129411. 
  11. ↑ 11.0 11.1 Hodgkin, A. L.; Huxley, A. F. (28 August 1952). "A quantitative description of membrane current and its application to conduction and excitation in nerve". The Journal of Physiology (Wiley) 117 (4): 500–544. doi:10.1113/jphysiol.1952.sp004764. ISSN 0022-3751. PMID 12991237. 
  12. ↑ Kerner, B. S.; Osipov, V. V. (1994). Autosolitons : a new approach to problems of self-organization and turbulence. Dordrecht Boston: Kluwer Academic. p. 53. ISBN 978-0-7923-2816-2. OCLC 30157395. 
  13. ↑ Bode, M.; Purwins, H.-G. (1995). "Pattern formation in reaction-diffusion systems - dissipative solitons in physical systems". Physica D: Nonlinear Phenomena (Elsevier BV) 86 (1–2): 53–63. doi:10.1016/0167-2789(95)00087-k. ISSN 0167-2789. Bibcode: 1995PhyD...86...53B. 
  14. ↑ Christov, C.I.; Velarde, M.G. (1995). "Dissipative solitons". Physica D: Nonlinear Phenomena (Elsevier BV) 86 (1–2): 323–347. doi:10.1016/0167-2789(95)00111-g. ISSN 0167-2789. Bibcode: 1995PhyD...86..323C. 
  15. ↑ Akhmediev, Nail, ed (2005). Dissipative Solitons. Lecture Notes in Physics. 661. Berlin, Heidelberg: Springer Berlin Heidelberg. doi:10.1007/b11728. ISBN 978-3-540-23373-2. 
  16. ↑ Radehaus, Ch.; Dirksmeyer, T.; Willebrand, H.; Purwins, H.-G. (1987). "Pattern formation in gas discharge systems with high impedance electrodes". Physics Letters A (Elsevier BV) 125 (2–3): 92–94. doi:10.1016/0375-9601(87)90128-9. ISSN 0375-9601. Bibcode: 1987PhLA..125...92R. 
  17. ↑ Brauer, I.; Bode, M.; Ammelt, E.; Purwins, H.-G. (1 April 2000). "Traveling Pairs of Spots in a Periodically Driven Gas Discharge System: Collective Motion Caused by Interaction". Physical Review Letters (American Physical Society) 84 (18): 4104–4107. doi:10.1103/physrevlett.84.4104. ISSN 0031-9007. PMID 10990621. Bibcode: 2000PhRvL..84.4104B. 
  18. ↑ Rubens, Sidney M.; Henderson, J. E. (1 August 1940). "The Characteristics and Function of Anode Spots in Glow Discharges". Physical Review (American Physical Society) 58 (5): 446–457. doi:10.1103/physrev.58.446. ISSN 0031-899X. Bibcode: 1940PhRv...58..446R. 
  19. ↑ Nasuno, Satoru (2003). "Dancing "atoms" and "molecules" of luminous gas-discharge spots". Chaos: An Interdisciplinary Journal of Nonlinear Science (AIP Publishing) 13 (3): 1010–1013. doi:10.1063/1.1604271. ISSN 1054-1500. PMID 12946194. Bibcode: 2003Chaos..13.1010N. 
  20. ↑ Jäger, D.; Baumann, H.; Symanczyk, R. (1986). "Experimental observation of spatial structures due to current filament formation in silicon pin diodes". Physics Letters A (Elsevier BV) 117 (3): 141–144. doi:10.1016/0375-9601(86)90021-6. ISSN 0375-9601. Bibcode: 1986PhLA..117..141J. 
  21. ↑ Mayer, K. M.; Parisi, J.; Huebener, R. P. (1988). "Imaging of self-generated multifilamentary current patterns in GaAs". Zeitschrift für Physik B (Springer Science and Business Media) 71 (2): 171–178. doi:10.1007/bf01312786. ISSN 0722-3277. Bibcode: 1988ZPhyB..71..171M. 
  22. ↑ Niedernostheide, F.-J.; Arps, M.; Dohmen, R.; Willebrand, H.; Purwins, H.-G. (1 June 1992). "Spatial and Spatio-Temporal Patterns in pnpn Semiconductor Devices" (in de). Physica Status Solidi B (Wiley) 172 (1): 249–266. doi:10.1002/pssb.2221720123. ISSN 0370-1972. Bibcode: 1992PSSBR.172..249N. 
  23. ↑ Beale, Marc (1993). "Uniform and filamentary transport in d.c. thin-film ZnS: Mn electroluminescent devices". Philosophical Magazine B (Informa UK Limited) 68 (5): 573–594. doi:10.1080/13642819308220144. ISSN 1364-2812. Bibcode: 1993PMagB..68..573B. 
  24. ↑ Taranenko, V. B.; Staliunas, K.; Weiss, C. O. (1 July 1997). "Spatial soliton laser: Localized structures in a laser with a saturable absorber in a self-imaging resonator". Physical Review A (American Physical Society) 56 (2): 1582–1591. doi:10.1103/physreva.56.1582. ISSN 1050-2947. Bibcode: 1997PhRvA..56.1582T. 
  25. ↑ Taranenko, V. B.; Staliunas, K.; Weiss, C. O. (14 September 1998). "Pattern Formation and Localized Structures in Degenerate Optical Parametric Mixing". Physical Review Letters (American Physical Society) 81 (11): 2236–2239. doi:10.1103/physrevlett.81.2236. ISSN 0031-9007. Bibcode: 1998PhRvL..81.2236T. 
  26. ↑ Schreiber, A.; Thüring, B.; Kreuzer, M.; Tschudi, T. (1997). "Experimental investigation of solitary structures in a nonlinear optical feedback system". Optics Communications (Elsevier BV) 136 (5–6): 415–418. doi:10.1016/s0030-4018(96)00722-5. ISSN 0030-4018. Bibcode: 1997OptCo.136..415S. 
  27. ↑ Schäpers, B.; Feldmann, M.; Ackemann, T.; Lange, W. (24 July 2000). "Interaction of Localized Structures in an Optical Pattern-Forming System". Physical Review Letters (American Physical Society) 85 (4): 748–751. doi:10.1103/physrevlett.85.748. ISSN 0031-9007. PMID 10991389. Bibcode: 2000PhRvL..85..748S. 
  28. ↑ Denz, Cornelia; Schwab, Michael; Weilnau, Carsten (2003). Transverse-Pattern Formation in Photorefractive Optics. Springer Tracts in Modern Physics. 188. Berlin, Heidelberg: Springer Berlin Heidelberg. doi:10.1007/b13583. ISBN 978-3-540-02109-4. 
  29. ↑ Barland, Stephane; Tredicce, Jorge R.; Brambilla, Massimo; Lugiato, Luigi A.; Balle, Salvador et al. (2002). "Cavity solitons as pixels in semiconductor microcavities". Nature (Springer Nature) 419 (6908): 699–702. doi:10.1038/nature01049. ISSN 0028-0836. PMID 12384692. Bibcode: 2002Natur.419..699B. 
  30. ↑ Zhang, H.; Tang, D. Y.; Zhao, L. M.; Wu, X.; Tam, H. Y. (6 January 2009). "Dissipative vector solitons in a dispersionmanaged cavity fiber laser with net positive cavity dispersion". Optics Express (The Optical Society) 17 (2): 455–60. doi:10.1364/oe.17.000455. ISSN 1094-4087. PMID 19158858. Bibcode: 2009OExpr..17..455Z. 
  31. ↑ Zhang, H.; Tang, D. Y.; Wu, X.; Zhao, L. M. (20 July 2009). "Multi-wavelength dissipative soliton operation of an erbium-doped fiber laser". Optics Express (The Optical Society) 17 (15): 12692–7. doi:10.1364/oe.17.012692. ISSN 1094-4087. PMID 19654674. Bibcode: 2009OExpr..1712692Z. 
  32. ↑ Hamik, Chad T.; Manz, Niklas; Steinbock, Oliver (2001). "Anomalous Dispersion and Attractive Pulse Interaction in the 1,4-Cyclohexanedione Belousov−Zhabotinsky Reaction†". The Journal of Physical Chemistry A (American Chemical Society) 105 (25): 6144–6153. doi:10.1021/jp010270j. ISSN 1089-5639. 
  33. ↑ Lane, Samuel L.; Luss, Dan (8 February 1993). "Rotating temperature pulse during hydrogen oxidation on a nickel ring". Physical Review Letters (American Physical Society) 70 (6): 830–832. doi:10.1103/physrevlett.70.830. ISSN 0031-9007. PMID 10054214. Bibcode: 1993PhRvL..70..830L. 
  34. ↑ Rotermund, H. H.; Jakubith, S.; von Oertzen, A.; Ertl, G. (10 June 1991). "Solitons in a surface reaction". Physical Review Letters (American Physical Society) 66 (23): 3083–3086. doi:10.1103/physrevlett.66.3083. ISSN 0031-9007. PMID 10043694. Bibcode: 1991PhRvL..66.3083R. 
  35. ↑ R. Suzuki, Adv. Biophys. 9 (1976): 115
  36. ↑ Dahlem, Markus A.; Hadjikhani, Nouchine (1 March 2009). Ben-Jacob, Eshel. ed. "Migraine Aura: Retracting Particle-Like Waves in Weakly Susceptible Cortex". PLOS ONE (Public Library of Science) 4 (4): e5007. doi:10.1371/journal.pone.0005007. ISSN 1932-6203. PMID 19337363. Bibcode: 2009PLoSO...4.5007D. 
  37. ↑ Umbanhowar, Paul B.; Melo, Francisco; Swinney, Harry L. (1996). "Localized excitations in a vertically vibrated granular layer". Nature (Springer Nature) 382 (6594): 793–796. doi:10.1038/382793a0. ISSN 0028-0836. Bibcode: 1996Natur.382..793U. 
  38. ↑ Lioubashevski, O.; Hamiel, Y.; Agnon, A.; Reches, Z.; Fineberg, J. (18 October 1999). "Oscillons and Propagating Solitary Waves in a Vertically Vibrated Colloidal Suspension". Physical Review Letters (American Physical Society) 83 (16): 3190–3193. doi:10.1103/physrevlett.83.3190. ISSN 0031-9007. Bibcode: 1999PhRvL..83.3190L. 
  39. ↑ Lioubashevski, O.; Arbell, H.; Fineberg, J. (20 May 1996). "Dissipative Solitary States in Driven Surface Waves". Physical Review Letters (American Physical Society) 76 (21): 3959–3962. doi:10.1103/physrevlett.76.3959. ISSN 0031-9007. PMID 10061156. Bibcode: 1996PhRvL..76.3959L. 
  40. ↑ Ahlers, Guenter (1991). "Experiments with pattern-forming systems". Physica D: Nonlinear Phenomena (Elsevier BV) 51 (1–3): 421–443. doi:10.1016/0167-2789(91)90249-9. ISSN 0167-2789. Bibcode: 1991PhyD...51..421A. 
  41. ↑ Melo, F.; Douady, S. (15 November 1993). "From solitary waves to static patterns via spatiotemporal intermittency". Physical Review Letters (American Physical Society) 71 (20): 3283–3286. doi:10.1103/physrevlett.71.3283. ISSN 0031-9007. PMID 10054934. Bibcode: 1993PhRvL..71.3283M. 
  42. ↑ J. Nagumo et al., Proc. Inst. Radio Engin. Electr. 50 (1962): 2061
  43. ↑ Purwins, H.-G.; Bödeker, H.U.; Liehr, A.W. (2004). "Dissipative Solitons in Reaction-Diffusion Systems". Dissipative Solitons. Lecture Notes on Physics. 661. Berlin, Heidelberg: Springer Berlin Heidelberg. pp. 267–308. doi:10.1007/10928028_11. ISBN 978-3-540-23373-2. 
  44. ↑ Meron, Ehud (1992). "Pattern formation in excitable media". Physics Reports (Elsevier BV) 218 (1): 1–66. doi:10.1016/0370-1573(92)90098-k. ISSN 0370-1573. Bibcode: 1992PhR...218....1M. 
  45. ↑ Niedernostheide, F.-J.; Dohmen, R.; Willebrand, H.; Schulze, H.-J.; Purwins, H.-G. (1992). "Pattern Formation in Nonlinear Physical Systems with Characteristic Electric Properties". Nonlinearity with disorder. Springer Proceedings in Physics. 67. Berlin, Heidelberg: Springer Berlin Heidelberg. pp. 282–309. doi:10.1007/978-3-642-84774-5_29. ISBN 978-3-642-84776-9. 
  46. ↑ 46.0 46.1 Gurevich, S. V.; Amiranashvili, Sh.; Purwins, H.-G. (1 November 2006). "Breathing dissipative solitons in three-component reaction-diffusion system". Physical Review E (American Physical Society) 74 (6): 066201. doi:10.1103/physreve.74.066201. ISSN 1539-3755. PMID 17280133. Bibcode: 2006PhRvE..74f6201G. 
  47. ↑ Or-Guil, Michal; G. Kevrekidis, Ioannis; Bär, Markus (2000). "Stable bound states of pulses in an excitable medium". Physica D: Nonlinear Phenomena (Elsevier BV) 135 (1–2): 154–174. doi:10.1016/s0167-2789(99)00136-0. ISSN 0167-2789. Bibcode: 2000PhyD..135..154O. 
  48. ↑ Schenk, C. P.; Or-Guil, M.; Bode, M.; Purwins, H.-G. (12 May 1997). "Interacting Pulses in Three-Component Reaction-Diffusion Systems on Two-Dimensional Domains". Physical Review Letters (American Physical Society) 78 (19): 3781–3784. doi:10.1103/physrevlett.78.3781. ISSN 0031-9007. Bibcode: 1997PhRvL..78.3781S. 
  49. ↑ Aranson, Igor S.; Kramer, Lorenz (4 February 2002). "The world of the complex Ginzburg-Landau equation". Reviews of Modern Physics (American Physical Society) 74 (1): 99–143. doi:10.1103/revmodphys.74.99. ISSN 0034-6861. Bibcode: 2002RvMP...74...99A. 
  50. ↑ Afanasjev, V. V.; Akhmediev, N.; Soto-Crespo, J. M. (1 January 1996). "Three forms of localized solutions of the quintic complex Ginzburg-Landau equation". Physical Review E (American Physical Society) 53 (2): 1931–1939. doi:10.1103/physreve.53.1931. ISSN 1063-651X. PMID 9964456. Bibcode: 1996PhRvE..53.1931A. 
  51. ↑ Rosanov, N. N.; Fedorov, S. V.; Shatsev, A. N. (2006). "Motion of clusters of weakly coupled two-dimensional cavity solitons". Journal of Experimental and Theoretical Physics (Pleiades Publishing) 102 (4): 547–555. doi:10.1134/s1063776106040030. ISSN 1063-7761. Bibcode: 2006JETP..102..547R. 
  52. ↑ Crasovan, L.-C.; Malomed, B. A.; Mihalache, D. (20 December 2000). "Stable vortex solitons in the two-dimensional Ginzburg-Landau equation". Physical Review E (American Physical Society) 63 (1): 016605. doi:10.1103/physreve.63.016605. ISSN 1063-651X. PMID 11304376. Bibcode: 2000PhRvE..63a6605C. 
  53. ↑ Soto-Crespo, J. M.; Akhmediev, N.; Ankiewicz, A. (2 October 2000). "Pulsating, Creeping, and Erupting Solitons in Dissipative Systems". Physical Review Letters (American Physical Society) 85 (14): 2937–2940. doi:10.1103/physrevlett.85.2937. ISSN 0031-9007. PMID 11005972. Bibcode: 2000PhRvL..85.2937S. 
  54. ↑ Soto-Crespo, J. M.; Akhmediev, Nail (18 December 2002). "Composite solitons and two-pulse generation in passively mode-locked lasers modeled by the complex quintic Swift-Hohenberg equation". Physical Review E (American Physical Society) 66 (6): 066610. doi:10.1103/physreve.66.066610. ISSN 1063-651X. PMID 12513432. Bibcode: 2002PhRvE..66f6610S. 
  55. ↑ Sakaguchi, Hidetsugu; Brand, Helmut R. (1996). "Stable localized solutions of arbitrary length for the quintic Swift-Hohenberg equation". Physica D: Nonlinear Phenomena (Elsevier BV) 97 (1–3): 274–285. doi:10.1016/0167-2789(96)00077-2. ISSN 0167-2789. Bibcode: 1996PhyD...97..274S. 
  56. ↑ Sakaguchi, Hidetsugu; Brand, Helmut R. (1998). "Localized patterns for the quintic complex Swift-Hohenberg equation". Physica D: Nonlinear Phenomena (Elsevier BV) 117 (1–4): 95–105. doi:10.1016/s0167-2789(97)00310-2. ISSN 0167-2789. Bibcode: 1998PhyD..117...95S. 
  57. ↑ Friedrich, Rudolf (2005). "Group Theoretic Methods in the Theory of Pattern Formation". Collective Dynamics of Nonlinear and Disordered Systems. Berlin/Heidelberg: Springer-Verlag. pp. 61–84. doi:10.1007/3-540-26869-3_4. ISBN 3-540-21383-X. https://archive.org/details/collectivedynami0000unse/page/61. 
  58. ↑ Bode, M (1997). "Front-bifurcations in reaction-diffusion systems with inhomogeneous parameter distributions". Physica D: Nonlinear Phenomena (Elsevier BV) 106 (3–4): 270–286. doi:10.1016/s0167-2789(97)00050-x. ISSN 0167-2789. Bibcode: 1997PhyD..106..270B. 
  59. ↑ Bode, M.; Liehr, A.W.; Schenk, C.P.; Purwins, H.-G. (2002). "Interaction of dissipative solitons: particle-like behaviour of localized structures in a three-component reaction-diffusion system". Physica D: Nonlinear Phenomena (Elsevier BV) 161 (1–2): 45–66. doi:10.1016/s0167-2789(01)00360-8. ISSN 0167-2789. Bibcode: 2002PhyD..161...45B. 
  60. ↑ Bödeker, H. U.; Röttger, M. C.; Liehr, A. W.; Frank, T. D.; Friedrich, R.; Purwins, H.-G. (28 May 2003). "Noise-covered drift bifurcation of dissipative solitons in a planar gas-discharge system". Physical Review E (American Physical Society) 67 (5): 056220. doi:10.1103/physreve.67.056220. ISSN 1063-651X. PMID 12786263. Bibcode: 2003PhRvE..67e6220B. 
  61. ↑ Bödeker, H U; Liehr, A W; Frank, T D; Friedrich, R; Purwins, H-G (15 June 2004). "Measuring the interaction law of dissipative solitons". New Journal of Physics (IOP Publishing) 6 (1): 62. doi:10.1088/1367-2630/6/1/062. ISSN 1367-2630. Bibcode: 2004NJPh....6...62B. 
  62. ↑ [1]

Books and overview articles

  • N. Akhmediev and A. Ankiewicz, Dissipative Solitons, Lecture Notes in Physics, Springer, Berlin (2005)
  • N. Akhmediev and A. Ankiewicz, Dissipative Solitons: From Optics to Biology and Medicine, Lecture Notes in Physics, Springer, Berlin (2008)
  • H.-G. Purwins et al., Advances in Physics 59 (2010): 485 doi:10.1080/00018732.2010.498228
  • A. W. Liehr: Dissipative Solitons in Reaction Diffusion Systems. Mechanism, Dynamics, Interaction. Volume 70 of Springer Series in Synergetics, Springer, Berlin Heidelberg 2013, ISBN:978-3-642-31250-2



Retrieved from "https://handwiki.org/wiki/index.php?title=Dissipative_soliton&oldid=3363743"