Double-star snark
| Double-star snark | |
|---|---|
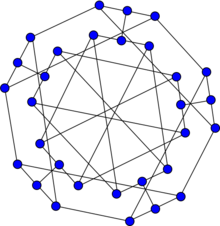 The Double-star snark | |
| Vertices | 30 |
| Edges | 45 |
| Radius | 4 |
| Diameter | 4 |
| Girth | 6 |
| Automorphisms | 80 |
| Chromatic number | 3 |
| Chromatic index | 4 |
| Book thickness | 3 |
| Queue number | 2 |
| Properties | Snark Hypohamiltonian |
| Table of graphs and parameters | |
In the mathematical field of graph theory, the double-star snark is a snark with 30 vertices and 45 edges.[1]
In 1975, Rufus Isaacs introduced two infinite families of snarks—the flower snark and the BDS snark, a family that includes the two Blanuša snarks, the Descartes snark and the Szekeres snark (BDS stands for Blanuša Descartes Szekeres).[2] Isaacs also discovered one 30-vertex snark that does not belong to the BDS family and that is not a flower snark — the double-star snark.
As a snark, the double-star graph is a connected, bridgeless cubic graph with chromatic index equal to 4. The double-star snark is non-planar and non-hamiltonian but is hypohamiltonian.[3] It has book thickness 3 and queue number 2.[4]
Gallery
The chromatic number of the double-star snark is 3.
The chromatic index of the double-star snark is 4.
References
- ↑ Weisstein, Eric W.. "Double Star Snark". http://mathworld.wolfram.com/DoubleStarSnark.html.
- ↑ Isaacs, R. (1975), "Infinite families of non-trivial trivalent graphs which are not Tait-colorable", American Mathematical Monthly (Mathematical Association of America) 82 (3): 221–239, doi:10.2307/2319844
- ↑ Weisstein, Eric W.. "Hypohamiltonian Graph". http://mathworld.wolfram.com/HypohamiltonianGraph.html.
- ↑ Wolz, Jessica; Engineering Linear Layouts with SAT. Master Thesis, University of Tübingen, 2018
 |  |
