Earth:Diffusion chronometry
Introduction
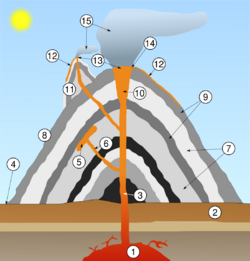
Diffusion chronometry is a geological technique that examines the chemical gradients within mineral crystals to estimate the duration of events in a magmatic system (e.g. magma mixing, magma decompression, magma degassing, etc.) and their associated eruptions. In simple terms, the mineral phenocryst acts as a "crystal clock" to determine how long a magmatic process took.[1] Diffusion chronometry takes advantage of the common chemical disequilibrium found in volcanic phenocrysts and examines their kinetic window to obtain timescale information.[2][3] Diffusion chronometry should not be confused with geospeedometry. Both utilize the theory of chemical diffusion, but the latter is more commonly used for analyzing rates of metamorphic events whereas the former is used to analyze features of eruptive events.
Eruptive events can occur on a time scale of days or months which, geologically speaking, is difficult to analyze using traditional radiometric dating techniques. The use of diffusion chronometry on past eruptions can help in forecasting eruptions by gaining a better understanding of the timescales of magmatic processes and can aid in determining timescales for volcano alert levels during an eruptive event.[4]
Kinetics
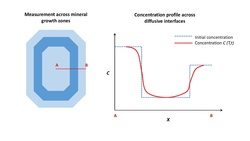
Chemical gradients in mineral crystals provide unique records of magmatic processes. These gradients can result from crystallization, differentiation, or magma mixing. Molecules and elements subsequently diffuse during magma storage at high temperatures, as the system attempts to return to equilibrium. If the diffusion coefficient of the element is known, the timescale of the magmatic process that formed the gradient can be calculated with Fick's second law of diffusion.[3][5][6] Fick's second law is:
,
where C is the concentration of the element in question, t is time, D is the diffusion coefficient, and x is lengthscale. A common analytical solution to Fick's second law that is used in diffusion chronometry is:[6][7]
,
where C is concentration at the current point, C1 is the concentration of the depleted region, C2 is the concentration of the enriched area, Erfc is the complementary error function, D is the diffusion coefficient, and t is the time. A common finite difference numerical solution to Fick's second law is:[5]
Where C2new is the concentration of the second point at the current timestep, C2old is the concentration of the second point at the previous timestep, C3old is the concentration of the next point at the previous timestep, C1old is the concentration of the previous point at the previous timestep, Δt is the timestep size in seconds, and Δx is the step distance, and D is the diffusion coefficient. If the (DΔt/Δx2) term is larger than 0.5, this finite-difference model is unstable and will not produce a usable result.
Experimental methods
The key requirement for diffusion chronometry is the availability and reliability of diffusion coefficients in silicate systems (mineral-melt). Experiments are performed in order to determine the diffusivity of an element in a mineral.[8] The three most common types of experiments are diffusion couple experiments, thin-film experiments, and powder source (constant surface) experiments.[8] In the diffusion couple experiment, two of the same minerals, with different concentrations of the intended diffusant element, are fused together and put in a high temperature furnace to induce diffusion across the mineral boundaries. Thin film experiments are set up with a thin film (nm to μm thickness) doped with the diffusant element is fused to the surface of the mineral and is put in a high temperature furnace to induce diffusion from the thin film to the mineral. The powder source experiments are set up with the mineral packed into and surrounded by a powder source doped in the diffusant element within an alumina or quartz glass crucible and placed in a high temperature furnace to induce diffusion from the powder source to the mineral. Experiments are typically run at varying temperatures (and to a lesser extent pressure and oxygen fugacity), with the goal of producing an Arrhenius plot. From the Arrhenius plot the frequency factor (D0) and the activation energy (Ea) can be determined for the specific mineral-element pair, these terms are then used in applying the diffusion equation to determine the diffusivity of the element in the mineral at the magmatic conditions of the system.
With the growth of new technology and therefore new experimental methods and analytical methods, the number of available element-mineral diffusivities are growing rapidly.[9]
Measuring diffusion profiles
Samples are typically prepared as thin sections or crystal separates. Thin sections are thin slices of rock (typically 30 μm thick) that allow for in-situ mineral analysis. Crystal separates are produced by crushing rock or sampling a tephra layer and then picking mineral grains, which are subsequently mounted in epoxy for analysis.
Major, trace, or isotopic compositions need to be measured with high precision (>10%) and high spatial resolution (~5 μm).[2] The relative abundance of the element of interest dictates the analytical method used.[10] Major elements (e.g. Fe-Mg in olivine, clinopyroxene, and orthopyroxene; Ca-Na in plagioclase feldspar), present at concentrations on the order of a few weight percent, are commonly analyzed by electron microprobe. Trace elements (e.g. Mg in plagioclase feldspar, H+ in olivine), present at concentrations on the order of parts per million, are typically measured by laser ablation inductively coupled plasma mass spectrometry (LA-ICP-MS) or Fourier-transform infrared spectroscopy (FTIR). Isotopic diffusion is commonly investigated with secondary-ion mass spectrometry (SIMS) or multi-collector LA-ICP-MS. When selecting analytical points for a diffusion profile, the spacing should be based on the ratio of diffusion length to spot size, which should exceed 2 to avoid convolution effects.[11]
Recent developments include the use of nanoscale secondary-ion mass spectrometry (NanoSIMS) for constraining elemental concentrations at sub-μm scale, two-dimensional elemental mapping with LA-ICP-MS, femto-second lasers, the atom probe, and computed tomography.[2]
Application
To apply diffusion chronometry, an appropriate mineral-element pair with a well-constrained diffusion coefficient must be chosen. Different mineral-element pairs exhibit very different diffusion coefficients, which correspond to varying timescales (from seconds to thousands of years) and record distinct magmatic processes. Temperature is the critical parameter, calculated with geothermobarometry, that determines the diffusion coefficient and subsequently the uncertainty of the timescale. Using experimentally derived D0 and Ea, temperature is plugged into the diffusion equation to get the diffusivity of the mineral-element pair in the system of question.
,
where D is the diffusion coefficient, D0 is the frequency factor specific to your mineral element pair, Ea is the activation energy in Joules, R is the gas constant, and T is temperature in Kelvin. This diffusivity (D) is then used in the appropriate analytical or numerical solutions to Fick's second law to calculate a timescale. Diffusion chronometry timescales typically have large uncertainties or ranges of timescales, but this information is critical when forecasting an eruption.[2]
Recent applications
The diffusion profiles of crystals within a single eruption have been used to constrain the time of magmatic processes at a variety of systems. This section will briefly highlight a number of studies where diffusion chronometry was successfully applied. Note that this list is not comprehensive.
Diffusion chronometry was applied to the 1999 eruption of Shishaldin volcano and displayed the connection between volcano monitoring signals and diffusion timescales from Fe-Mg interdiffusion in olivines from the eruptive product.[12] Diffusion timescales showed that eruption run-up started 9 months before the eruption, with more immediate run-up occurring 50 and 10 days prior to the eruption. The 9-month diffusion timescales correlate well with the start of deep earthquakes, a typical precursor to eruption, the ~50 day timescales correlate well with a temperature anomaly (i.e. intruding magma), steam, and a 5.2 magnitude earthquake, and the ~10 day timescales correspond to rapid remobilization of the magma during its final ascent to the surface. This study by Rasmussen and colleagues in 2018,[12] is a prime example of how diffusion chronometry can aid in forecasting volcanic eruptions.
Shamloo and Till (2019)[13] applied Ba and Sr in sanidine and Ti in quartz diffusion chronometry to the Lava Creek Tuff in Yellowstone Caldera, to understand the timing of eruption triggers for super eruptions. Here they determined that the super eruption occurred years to at most a decade after magma rejuvenation occurred, triggering the Lava Creek Tuff super eruption.
Diffusion chronometry profiles helped reconstruct the dynamics of the magma plumbing system underneath Mount Etna during 1991-1993.[14] This study employed Fe-Mg interdiffusion in olivines to determine the timescales of magmatic processes that a number of crystal populations experienced and determined 3 significant timescales. The first timescale tracked magma transfer between differing magmas and occurred 3–6 months before eruption. The second timescale is a short residence time of less than a month which is thought to be the final mixing process. The third and longest timescale, up to 1 year, represents crystals that were recycled through different magmatic environments prior to eruption.
References
- ↑ Rosen, Julia (2016-11-18). "Crystal clocks" (in en). Science 354 (6314): 822–825. doi:10.1126/science.354.6314.822. ISSN 0036-8075. PMID 27856862. https://www.science.org/doi/10.1126/science.354.6314.822.
- ↑ 2.0 2.1 2.2 2.3 Costa, F.; Shea, T.; Ubide, T. (2020-04-01). "Diffusion chronometry and the timescales of magmatic processes" (in en). Nature Reviews Earth & Environment 1 (4): 201–214. doi:10.1038/s43017-020-0038-x. ISSN 2662-138X. https://www.nature.com/articles/s43017-020-0038-x.
- ↑ 3.0 3.1 Chakraborty, Sumit (2008-05-01). "Diffusion in Solid Silicates: A Tool to Track Timescales of Processes Comes of Age" (in en). Annual Review of Earth and Planetary Sciences 36 (1): 153–190. doi:10.1146/annurev.earth.36.031207.124125. ISSN 0084-6597. https://www.annualreviews.org/doi/10.1146/annurev.earth.36.031207.124125.
- ↑ Winson, Annie E G; Costa, Fidel; Newhall, Christopher G; Woo, Gordon (December 2014). "An analysis of the issuance of volcanic alert levels during volcanic crises" (in en). Journal of Applied Volcanology 3 (1): 14. doi:10.1186/s13617-014-0014-6. ISSN 2191-5040.
- ↑ 5.0 5.1 Costa, F.; Shea, T.; Ubide, T. (April 2020). "Diffusion chronometry and the timescales of magmatic processes" (in en). Nature Reviews Earth & Environment 1 (4): 201–214. doi:10.1038/s43017-020-0038-x. ISSN 2662-138X. https://www.nature.com/articles/s43017-020-0038-x.
- ↑ 6.0 6.1 Lasaga, Antonio C. (1998-12-31). Kinetic Theory in the Earth Sciences. Princeton University Press. doi:10.1515/9781400864874. ISBN 978-1-4008-6487-4. https://www.degruyter.com/document/doi/10.1515/9781400864874/html.
- ↑ Crank, John (1979). The Mathematics of Diffusion (1st ed.). Oxford Science Publications. ISBN 9780198534112.
- ↑ 8.0 8.1 Watson, E. Bruce; Baker, Don R. (1991), Perchuk, Leonid L.; Kushiro, Ikuo, eds., "Chemical Diffusion in Magmas: An Overview of Experimental Results and Geochemical Applications", Physical Chemistry of Magmas, Advances in Physical Geochemistry (New York, NY: Springer New York) 9: pp. 120–151, doi:10.1007/978-1-4612-3128-8_4, ISBN 978-1-4612-7806-1, http://link.springer.com/10.1007/978-1-4612-3128-8_4, retrieved 2023-05-11
- ↑ Brady, J. B.; Cherniak, D. J. (2010-01-01). "Diffusion in Minerals: An Overview of Published Experimental Diffusion Data" (in en). Reviews in Mineralogy and Geochemistry 72 (1): 899–920. doi:10.2138/rmg.2010.72.20. ISSN 1529-6466. https://pubs.geoscienceworld.org/rimg/article/72/1/899-920/140905.
- ↑ Cherniak, D. J.; Hervig, R.; Koepke, J.; Zhang, Y.; Zhao, D. (2010-01-01). "Analytical Methods in Diffusion Studies" (in en). Reviews in Mineralogy and Geochemistry 72 (1): 107–170. doi:10.2138/rmg.2010.72.4. ISSN 1529-6466. https://pubs.geoscienceworld.org/rimg/article/72/1/107-170/140878.
- ↑ Bradshaw, Richard W.; Kent, Adam J.R. (September 2017). "The analytical limits of modeling short diffusion timescales" (in en). Chemical Geology 466: 667–677. doi:10.1016/j.chemgeo.2017.07.018. https://linkinghub.elsevier.com/retrieve/pii/S0009254117304163.
- ↑ 12.0 12.1 Rasmussen, Daniel J.; Plank, Terry A.; Roman, Diana C.; Power, John A.; Bodnar, Robert J.; Hauri, Erik H. (March 2018). "When does eruption run-up begin? Multidisciplinary insight from the 1999 eruption of Shishaldin volcano" (in en). Earth and Planetary Science Letters 486: 1–14. doi:10.1016/j.epsl.2018.01.001. https://linkinghub.elsevier.com/retrieve/pii/S0012821X18300050.
- ↑ Shamloo, Hannah I.; Till, Christy B. (April 2019). "Decadal transition from quiescence to supereruption: petrologic investigation of the Lava Creek Tuff, Yellowstone Caldera, WY" (in en). Contributions to Mineralogy and Petrology 174 (4): 32. doi:10.1007/s00410-019-1570-x. ISSN 0010-7999. http://link.springer.com/10.1007/s00410-019-1570-x.
- ↑ Kahl, Maren; Chakraborty, Sumit; Costa, Fidel; Pompilio, Massimo (August 2011). "Dynamic plumbing system beneath volcanoes revealed by kinetic modeling, and the connection to monitoring data: An example from Mt. Etna" (in en). Earth and Planetary Science Letters 308 (1–2): 11–22. doi:10.1016/j.epsl.2011.05.008. https://linkinghub.elsevier.com/retrieve/pii/S0012821X11002792.
 |
