Engineering:Differentiator

Short description: Type of circuit

In electronics, a differentiator is a circuit designed to produce an output approximately proportional to the rate of change (the time derivative) of the input. A true differentiator cannot be physically realized, because it has infinite gain at infinite frequency. A similar effect can be achieved, however, by limiting the gain above some frequency. The differentiator circuit is essentially a high-pass filter. An active differentiator includes some form of amplifier, while a passive differentiator is made only of resistors, capacitors and inductors.

Passive differentiator

The simple four-terminal passive circuits depicted in figure, consisting of a resistor and a capacitor, or alternatively a resistor and an inductor, behave as differentiators.

Capacitive differentiator

Inductive differentiator

Indeed, according to Ohm's law, the voltages at the two ends of the capacitive differentiator are related by a transfer function that has a zero in the origin and a pole in −[math]\displaystyle{ \tfrac{1}{RC} }[/math] and that is consequently a good approximation of an ideal differentiator at frequencies below the natural frequency of the pole:

[math]\displaystyle{ Y=\frac{Z_R}{Z_R+Z_C}X =\frac{R}{R+\frac{1}{sC}}X =\frac{sRC}{1+sRC}X \implies Y\approx sRCX \quad \text{for} \ |s|\ll \frac{1}{RC} }[/math]

Similarly, the transfer function of the inductive differentiator has a zero in the origin and a pole in −[math]\displaystyle{ \tfrac{R}{L} }[/math].

Frequency response function of the passive differentiator circuits. [math]\displaystyle{ \omega_0 =\tfrac{1}{RC} }[/math] for the capacitive circuit, while [math]\displaystyle{ \omega_0 =\tfrac{R}{L} }[/math] for the inductive circuit

Active differentiator

Ideal differentiator

Ideal differentiator.

A differentiator circuit (also known as a differentiating amplifier or inverting differentiator) consists of an ideal operational amplifier with a resistor R providing negative feedback and a capacitor C at the input, such that:

• [math]\displaystyle{ V_\text{in} }[/math] is the voltage across C (from the op amp's virtual ground negative terminal).
• [math]\displaystyle{ V_\text{out} }[/math] is the voltage across R (also from the op amp's virtual ground negative terminal).
• [math]\displaystyle{ I }[/math] is the current flowing from the output through both R and C to the circuit's input.
  • No current flows into the ideal op amp's inputs because they have very high input impedance.

By utilizing the capacitor's current–voltage relation, this circuit's current [math]\displaystyle{ I }[/math] flowing from the output to the input will be proportional to the derivative of the voltage across the capacitor:

[math]\displaystyle{ I = C \, \frac{dV_\text{in}}{dt} \, , }[/math]

This same current [math]\displaystyle{ I }[/math] is converted into a voltage when it passes through the resistor according to ohm's law:

[math]\displaystyle{ V_\text{out} = -IR \, , }[/math]

Inserting the capacitor's equation for [math]\displaystyle{ I }[/math] provides the output voltage as a function of the input voltage:

[math]\displaystyle{ V_\text{out} = -RC \frac{dV_\text{in}}{dt}. }[/math]

Consequently,

• The output voltage is proportional to the time derivative of the input voltage with a gain of [math]\displaystyle{ RC . }[/math] Hence, the circuit acts as a differentiator and amplifier.
• The negative sign indicates the output has a 180° phase shift (inversion) with respect to the input.
• The equation is true for any frequency signal, assuming an ideal op amp (though a real op-amp has limited bandwidth).

The op amp's low-impedance output isolates the load of the succeeding stages, so this circuit has the same response independent of its load.

If a constant DC voltage is applied as input, the output voltage is zero. If the input voltage changes from zero to negative, the output voltage is positive. If the applied input voltage changes from zero to positive, the output voltage is negative. If a square-wave input is applied to a differentiator, then a spike waveform is obtained at the output.

Operation as high pass filter

Treating the capacitor as an impedance with capacitive reactance of X_c = 1/2πfC allows analyzing the differentiator as a high pass filter. The inverse-proportionality to frequency means that at low frequency, the reactance of a capacitor is high, and at high frequency reactance is low. Since the feedback configuration provides a gain of R_f/X_c, that means the gain is low at low frequencies (or for slow changing input), and higher at higher frequencies (or for fast changing input).

Frequency response

The transfer function of an ideal differentiator is [math]\displaystyle{ \frac{V_\text{out}}{V_\text{in}} = -sRC }[/math], and the Bode plot of its magnitude is:

Advantages

A small time constant is sufficient to cause differentiation of the input signal

Limitations

At high frequencies:

• this simple differentiator circuit becomes unstable and starts to oscillate;
• the circuit becomes sensitive to noise, that is, when amplified, noise dominates the input/message signal.

Practical differentiator

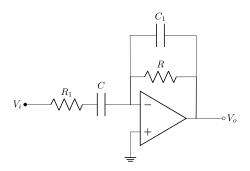
In order to overcome the limitations of the ideal differentiator, an additional small-value capacitor C₁ is connected in parallel with the feedback resistor R, which prevents the differentiator circuit from oscillating, and a resistor R₁ is connected in series with the capacitor C, which limits the increase in gain to a ratio of R/R₁.

Since negative feedback is present through the resistor R, we can apply the virtual ground concept, that is, the voltage at the inverting terminal = voltage at the non-inverting terminal = 0.

Applying nodal analysis, we get

[math]\displaystyle{ \frac{0 - V_o}{R} + \frac{0 - V_o}{\frac{1}{sC_1}} + \frac{0 - V_i}{R_1 + \frac{1}{sC}} = 0, }[/math]

[math]\displaystyle{ -V_o \left(\frac{1}{R} + sC_1\right) = \frac{V_i}{R_1 + \frac{1}{sC}}. }[/math]

Therefore,

[math]\displaystyle{ \frac{V_o}{V_i} = \frac{-sRC}{(1 + sR_1C)(1 + sRC_1)}. }[/math]

Hence, there occurs one zero at [math]\displaystyle{ s = 0 }[/math] and two poles at [math]\displaystyle{ s = f_1 = \tfrac{1}{2\pi R_1C} }[/math] and [math]\displaystyle{ s = f_2 = \tfrac{1}{2\pi RC_1} }[/math].

Frequency response

This practical differentiator's frequency response is a band-pass filter:

From the above plot, it can be seen that:

• Below [math]\displaystyle{ \omega_1 }[/math], the circuit attenuates and acts as a differentiator.
• Between [math]\displaystyle{ \omega_1 }[/math] and [math]\displaystyle{ \omega_2 }[/math], the circuit acts as a voltage follower or buffer.
• Above [math]\displaystyle{ \omega_2 }[/math], the circuit attenuates and acts as an integrator.

Setting [math]\displaystyle{ RC_1 = R_1C = RC }[/math] will produce one zero at [math]\displaystyle{ s = 0 }[/math] and two poles at [math]\displaystyle{ s = f_a = \tfrac{1}{2\pi RC} }[/math], resulting in the following frequency response:

From the above plot, we observe that:

• Below [math]\displaystyle{ \omega_1 }[/math], the circuit acts as a differentiator;
• Above [math]\displaystyle{ \omega_1 }[/math], the circuit acts as an integrator.

Applications

The differentiator circuit is essentially a high-pass filter. It can generate a square wave from a triangle wave input and produce alternating-direction voltage spikes when a square wave is applied. In ideal cases, a differentiator reverses the effects of an integrator on a waveform, and conversely. Hence, they are most commonly used in wave-shaping circuits to detect high-frequency components in an input signal. Differentiators are an important part of electronic analogue computers and analogue PID controllers. They are also used in frequency modulators as rate-of-change detectors.

A passive differentiator circuit is one of the basic electronic circuits, being widely used in circuit analysis based on the equivalent circuit method.

See also

• Integrator
• Inverting differentiator at op amp applications