Engineering:Intrinsic bond orbitals
Intrinsic bond orbitals (IBO) are localized molecular orbitals giving exact and non-empirical representations of wave functions. They are obtained by unitary transformation and form an orthogonal set of orbitals localized on a minimal number of atoms. IBOs present an intuitive and unbiased interpretation of chemical bonding with naturally arising Lewis structures.[1] For this reason IBOs have been successfully employed for the elucidation of molecular structures[1] and electron flow along the intrinsic reaction coordinate (IRC).[2] IBOs have also found application as Wannier functions in the study of solids.[3][4]
Theory
The IBO method entails molecular wave-functions calculated using self-consistent field (SCF) methods such as Kohn-Sham density functional theory (DFT) which are expressed as linear combinations of localized molecular orbitals.[1][5]
In order to arrive at IBOs, intrinsic atomic orbitals (IAOs) are first calculated as representations of a molecular wave function for which each IAO can be assigned to a specific atom. This allows for a chemically intuitive orbital picture as opposed to the commonly used large and diffuse basis sets for the construction of more complex molecular wavefunctions.[5]
IAOs are constructed from tabulated free-atom AOs of standard basis-sets under consideration of the molecular environment. This yields polarized atomic orbitals that resemble the free-atom AOs as much as possible, before orthonormalization of the polarized AOs results in the set of IAOs. IAOs are thus a minimal basis for a given molecule in which atomic contributions can be distinctly assigned. The sum of all IAOs spans exactly over the molecular orbitals which renders them an exact representation of the wavefunction.[5] Since IAOs are associated with a specific atom, they can provide atom specific properties such as the partial charge. Compared to other charges, such as the Mulliken charge, the IAO charges are independent of the employed basis set.[1]
IBOs are constructed as a linear combination over IAOs with the condition of minimizing the number of atoms over which the orbital charge is spread. Each IBO can thereby be divided into the contributions of the atoms as the electronic occupation of orbital on atom . The localization is performed in the spirit of the Pipek-Mezey localization scheme, maximizing a localization functional .[1]
with or . While the choice of the exponent does not affect the resulting IBOs in most cases, the choice of localizes the orbitals in aromatic systems unlike .[1]
The process of IBO construction is performed by unitary tranfomation of canonical MOs, which ensures that the IBOs remain an exact and physically accurate representation of the molecular wavefunction due to the invariance of Slater determinant wavefunctions towards unitary rotations.
The unitary matrix , which produces the localized IBOs upon matrix multiplication with set of occupied MOs , is thereby chosen to effectively minimize spread of IBOs over the atoms of a molecule. The product is a set of localized IBOs, closely resembling the chemically intuitive shapes of molecular orbitals, allowing for distinction of bond types, atomic contributions and polarization.[1]
Application in structure and bonding
In his original paper introducing IBOs, Knizia showed the versatility of his method for describing not only classical bonding situations, such as the σ and π bond, but also aromatic systems and non-trivial bonds. The differentiation of σ and π bonds in acrylic acid is possible based on IBO geometries, as are the identification of the IBOs corresponding to the oxygen lone pairs. Benzene provided an example of a delocalized aromatic system to test the IBO method. Apart from the C-C and C-H σ-bonds, the six electron π-system is expressed as three delocalized IBOs. Representation of non-Lewis bonding was demonstrated on diborane B2H6, with one IBO stretching over B-H-B, corresponding to the 3-center-2-electron bond.[1]


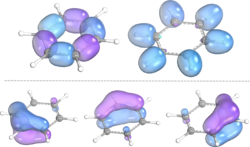
Transition metal compounds
IBO analysis was used to explain the stability of electron rich gold-carbene complexes, mimicking reactive intermediates in gold catalysis. While these complexes are sometimes depicted with a Au-C double bond, representing the sigma donation of the carbene and π backbonding of Au, IBO analysis points towards a minimal amount of π-backbonding with the respective orbital mainly localized on Au. The σ-donating carbene orbital is likewise strongly polarized towards C. Stabilization of the compound thus occurs through strong donation of the aromatic carbene substituents into the carbene carbon p-orbitals, outcompeting the Au-π-backdonation. IBO analysis was thus able to negate the double bond character of the gold-carbene complexes and provided deep insight into the electronic structure of Cy3P-Au-C(4-OMe-C6H4)2) (Cy = cyclohexyl).[5]
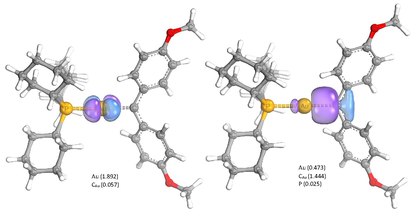
The π-backbonding character was again evaluated for gold-vinylidene complexes, as another common type of gold catalysis intermediates. IBO analysis revealed significantly stronger π-backbonding for the gold-vinylidenes compared to the gold-carbenes. This was attributed to the geometric inability of aromatic vinylidene substituents to compete with Au for π-interactions since the respective orbitals are perpendicular to each other.[6]
Knizia and Klein similarly employed IBO for the analysis of [Fe(CO)3NO]–. The even polarization of IBOs between Fe and N points towards a covalently bonded NO ligand. The double bond occurs via two d-p π-interactions and results in a formal Fe0 center. Confirmed by further calculations, IBO proved as a fast and straightforward method to interpret bonding in this case.[7] Making use of the low computational cost, a Cloke-Wilson rearrangement catalyzed by [Fe(CO)3NO]– was investigated by constructing the IBOs for every stationary point along the IRC. It was found that one of the Fe-NO π bonds takes active part in catalysis by electron transfer to and from the substrate, explaining the unique catalytic activity of [Fe(CO)3NO]– compared to the isoelectronic [Fe(CO)4]2–.[8]
Apart from the above mentioned compounds, the IBO method has been employed to investigate various other transition metal complexes, such as gold-diarylallenylidenes[5] or diplatinum diboranyl complexes,[9] proving as a valuable tool to gain insight into the extent and nature of bonding.
Main group compounds

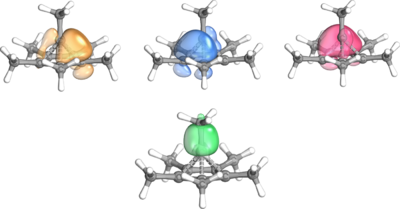
IBO analysis has been employed in main group chemistry to elucidate oftentimes non-trivial electronic structure. The bonding of phosphaaluminirenes was, for example, investigated showing a 3-center-2π-electron bond of the AlCP cycle.[12] Further application was found for confirming the distonic nature of a phosphorus containing radical cation reported by Chen et al. (see figure). While the IAO charge analysis yielded a positive charge on the chelated P, IBOs showed the localization of the unpaired electron on the other P atom, confirming the spatial separation of radical site and charge.[13]
Another example is the elucidation of the electronic structure of the hexamethylbenzene dication. Three π bonding IBOs were found between the basal C5Me5 plane and the apical C, reminiscent of Cp* coordination complexes. The three π bonds are thereby polarized towards the apical C, which in turn coordinates to a CH3+ cation with its lone pair. IBO analysis therefore revealed the Lewis-acidic and Lewis-basic character of the apical C.[14]
Applications of IBO for cluster compounds have included zirconium doped boron clusters. IBO analysis showed, that the unusual stability of the neutral ZrB12 cluster stems from several multicenter σ bonds. The B-B σ bonding orbitals extend to the central Zr atom, forming the mulicenter bonds. This example displays the method's aptitude to analyze cluster compounds and multicenter bonding.[15]
Valence virtual intrinsic bond orbitals
Although IBOs typically describe occupied orbitals, the description of unoccupied orbitals can likewise be of value for interpreting chemical interactions. Valence virtual IBOs (vvIBOs) were introduced with the investigation of high valent formal Ni(IV) complexes. The bonding and antibonding manifold of the compound were described using IBOs and vvIBOs respectively. Compared to the widely used HOMO/LUMOs which are often spread over the whole molecule and can be difficult to interpret, vvIBOs allow for more direct interpretation of chemical interactions with unoccupied orbitals.[16]
Electron flow along the IRC
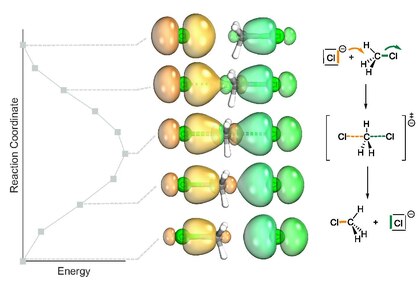
In 2015, Knizia and Klein introduced the analysis of electron flow in reactions with IBO as a non-empirical and straight-forward method of evaluating curly arrow mechanisms. Since IBOs are exact representations of Kohn-Sham wavefunctions, they can provide physical confirmation for curly arrows mechanisms based on first-principles. IBOs usually represent chemical bonds and lone pairs, this method allows for elucidation of bond rearrangements in terms of the elemental steps and their sequence. By calculating the root mean square deviations of the partial charge distributions compared to the initial charge distribution, IBOs taking active part in a reaction can be distinguished from those that remain unchanged along the IRC.[2]
Knizia and Klein demonstrate the versatility of this method in their original report, first presenting a simple SN2-type self-exchange reaction of H3CCl and Cl–, followed by the migration of π bonds in a substitution reaction (SN2) and π- to σ-bond transformations in a Claisen rearrangement. Electron flow can be easily followed by observing the migration of an IBO and bond types are easily distinguished based on the geometries of the IBOs. The value of IBO analysis along the IRC[2] especially shows for complex reactions, such as a cyclopropanation reaction with only one transition state and without intermediates, reported by Haven et al.[17] Calculations by Knizia and Klein yielded a precise curly arrow mechanism for this reaction.[2]
Closed-shell systems
Examples of IBO analysis along the IRC included the investigation of C-H bond activation by gold-vinylidene complexes. Through this method, it is possible to discern between concerted and stepwise reactions. The previously thought single step C-H activation reaction was in this case revealed to consist of three distinct phases: i) hydride transfer, ii) C-C bond formation and iii) sigma to pi rearrangement of the lone pair coordinated to Au.[18]
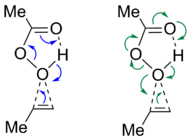
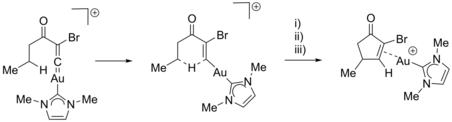
Other reports of IBO analysis along the IRC include the elucidation and confirmation of a previously proposed mechanism for a [3,3]-sigmatropic rearrangement of a Au(I)-vinyl species[20] or the epoxidation of alkene by peracids.[19] For the latter, the textbook four curly arrow mechanism was found to be physically inaccurate. Instead, seven changing IBOs were found, yielding an ideal mechanism featuring seven curly arrows.[19] The combination of IBO analysis with other computational methods, such as natural bond orbital (NBO) analysis for a Ti-catalyzed pyrrole synthesis[21] or natural localized molecular orbital (NLMO) analysis for an intramolecular cycloaddition of a phosphaalkene to an arene has likewise led to insightful results regarding the specifics of the reaction mechanisms.[22]

Open-shell systems
Klein and Knizia furthermore introduced the first examples of IBOs used for analysis of open-shell systems during proton-coupled electron transfer (PCET) and hydrogen atom transfer (HAT). The differentiation between pCET, a separate but concerted electron and proton transfer, and HAT, the transfer of a hydrogen atom, were shown for two well-studied model systems of enzymatic Fe-oxo active sites. IBOs along the IRC were calculated for the alpha and beta spin manifold respectively. While the IBO of the alpha spin electron travelled together with the proton to take part in the formation of a new H-O bond in case of HAT, the electron was transferred to the Fe-center separated from the transferred proton for PCET. The successful application of the IBO method for these two examples of open-shell systems was suggested to pave the way for broader applications to similar problems.[23]
See also
References
- ↑ 1.00 1.01 1.02 1.03 1.04 1.05 1.06 1.07 1.08 1.09 1.10 Knizia, Gerald (2013-11-12). "Intrinsic Atomic Orbitals: An Unbiased Bridge between Quantum Theory and Chemical Concepts" (in en). Journal of Chemical Theory and Computation 9 (11): 4834–4843. doi:10.1021/ct400687b. ISSN 1549-9618. PMID 26583402. https://pubs.acs.org/doi/10.1021/ct400687b.
- ↑ 2.0 2.1 2.2 2.3 2.4 Knizia, Gerald; Klein, Johannes E. M. N. (2015-04-27). "Electron Flow in Reaction Mechanisms-Revealed from First Principles" (in en). Angewandte Chemie International Edition 54 (18): 5518–5522. doi:10.1002/anie.201410637. PMID 25737294. https://onlinelibrary.wiley.com/doi/10.1002/anie.201410637.
- ↑ Schäfer, Tobias; Gallo, Alejandro; Irmler, Andreas; Hummel, Felix; Grüneis, Andreas (28 December 2021). "Surface science using coupled cluster theory via local Wannier functions and in-RPA-embedding: The case of water on graphitic carbon nitride". The Journal of Chemical Physics 155 (24). doi:10.1063/5.0074936.
- ↑ Wöckinger, Benjamin; Rumpf, Alexander; Schäfer, Tobias (16 October 2025). "Convergence and Properties of Intrinsic Bond Orbitals in Solids". Journal of Chemical Theory and Computation. doi:10.1021/acs.jctc.5c00130. https://pubs.acs.org/doi/10.1021/acs.jctc.5c00130.
- ↑ 5.0 5.1 5.2 5.3 5.4 5.5 Nunes dos Santos Comprido, Laura; Klein, Johannes E. M. N.; Knizia, Gerald; Kästner, Johannes; Hashmi, A. Stephen K. (2015-08-24). "The Stabilizing Effects in Gold Carbene Complexes" (in en). Angewandte Chemie International Edition 54 (35): 10336–10340. doi:10.1002/anie.201412401. PMID 25951142. https://onlinelibrary.wiley.com/doi/10.1002/anie.201412401.
- ↑ Nunes dos Santos Comprido, Laura; Klein, Johannes E. M. N.; Knizia, Gerald; Kästner, Johannes; Hashmi, A. Stephen K. (2016-02-24). "Gold(I) Vinylidene Complexes as Reactive Intermediates and Their Tendency to π-Backbond" (in en). Chemistry - A European Journal 22 (9): 2892–2895. doi:10.1002/chem.201504511. PMID 26711532. https://onlinelibrary.wiley.com/doi/10.1002/chem.201504511.
- ↑ Klein, Johannes E. M. N.; Miehlich, Burkhard; Holzwarth, Michael S.; Bauer, Matthias; Milek, Magdalena; Khusniyarov, Marat M.; Knizia, Gerald; Werner, Hans-Joachim et al. (2014-02-10). "The Electronic Ground State of [Fe(CO) 3 (NO) − : A Spectroscopic and Theoretical Study"] (in en). Angewandte Chemie International Edition 53 (7): 1790–1794. doi:10.1002/anie.201309767. PMID 24482198. https://onlinelibrary.wiley.com/doi/10.1002/anie.201309767.
- ↑ Klein, Johannes E. M. N.; Knizia, Gerald; Miehlich, Burkhard; Kästner, Johannes; Plietker, Bernd (2014-06-10). "Fe or FeNO Catalysis? A Quantum Chemical Investigation of the [Fe(CO) 3 (NO) − -Catalyzed Cloke-Wilson Rearrangement"] (in en). Chemistry - A European Journal 20 (24): 7254–7257. doi:10.1002/chem.201402716. PMID 24817507. https://onlinelibrary.wiley.com/doi/10.1002/chem.201402716.
- ↑ Braunschweig, Holger; Dewhurst, Rian D.; Jiménez-Halla, J. Oscar C.; Matito, Eduard; Muessig, Jonas H. (2018-01-08). "Transition-Metal π-Ligation of a Tetrahalodiborane" (in en). Angewandte Chemie International Edition 57 (2): 412–416. doi:10.1002/anie.201709515. PMID 29134749. https://onlinelibrary.wiley.com/doi/10.1002/anie.201709515.
- ↑ Liu, Liu Leo; Zhou, Jiliang; Cao, Levy L.; Stephan, Douglas W. (2019-10-23). "Phosphaaluminirenes: Synthons for Main Group Heterocycles" (in en). Journal of the American Chemical Society 141 (42): 16971–16982. doi:10.1021/jacs.9b09330. ISSN 0002-7863. PMID 31557435. https://pubs.acs.org/doi/10.1021/jacs.9b09330.
- ↑ Chen, Xiaodan; Liu, Liu Leo; Liu, Shihua; Grützmacher, Hansjörg; Li, Zhongshu (2020-10-19). "A Room‐Temperature Stable Distonic Radical Cation". Angewandte Chemie 132 (52): 24038–24043. doi:10.1002/ange.202011677. ISSN 0044-8249. http://dx.doi.org/10.1002/ange.202011677.
- ↑ Liu, Liu Leo; Zhou, Jiliang; Cao, Levy L.; Stephan, Douglas W. (2019-10-23). "Phosphaaluminirenes: Synthons for Main Group Heterocycles" (in en). Journal of the American Chemical Society 141 (42): 16971–16982. doi:10.1021/jacs.9b09330. ISSN 0002-7863. PMID 31557435. https://pubs.acs.org/doi/10.1021/jacs.9b09330.
- ↑ Chen, Xiaodan; Liu, Liu Leo; Liu, Shihua; Grützmacher, Hansjörg; Li, Zhongshu (2020-10-19). "A Room‐Temperature Stable Distonic Radical Cation". Angewandte Chemie 132 (52): 24038–24043. doi:10.1002/ange.202011677. ISSN 0044-8249. http://dx.doi.org/10.1002/ange.202011677.
- ↑ 14.0 14.1 Klein, Johannes E. M. N.; Havenith, Remco W. A.; Knizia, Gerald (2018-08-22). "The Pentagonal-Pyramidal Hexamethylbenzene Dication: Many Shades of Coordination Chemistry at Carbon" (in en). Chemistry - A European Journal 24 (47): 12340–12345. doi:10.1002/chem.201705812. PMID 29341342.
- ↑ Sun, Weiguo; Xia, Xinxin; Lu, Cheng; Kuang, Xiaoyu; Hermann, Andreas (2018). "Probing the structural and electronic properties of zirconium doped boron clusters: Zr distorted B 12 ligand framework" (in en). Physical Chemistry Chemical Physics 20 (36): 23740–23746. doi:10.1039/C8CP03384F. ISSN 1463-9076. PMID 30198528. Bibcode: 2018PCCP...2023740S. http://xlink.rsc.org/?DOI=C8CP03384F.
- ↑ Steen, Jelte S.; Knizia, Gerald; Klein, Johannes E. M. N. (2019-09-09). "σ‐Noninnocence: Masked Phenyl‐Cation Transfer at Formal Ni IV" (in en). Angewandte Chemie 131 (37): 13267–13273. doi:10.1002/ange.201906658. ISSN 0044-8249.
- ↑ Haven, Tobias; Kubik, Grzegorz; Haubenreisser, Stefan; Niggemann, Meike (2013-04-02). "Calcium-Catalyzed Cyclopropanation" (in en). Angewandte Chemie International Edition 52 (14): 4016–4019. doi:10.1002/anie.201209053. PMID 23450731. https://onlinelibrary.wiley.com/doi/10.1002/anie.201209053.
- ↑ 18.0 18.1 Klein, Johannes E. M. N.; Knizia, Gerald; Nunes dos Santos Comprido, Laura; Kästner, Johannes; Hashmi, A. Stephen K. (2017-11-13). "C(sp 3 )−H Bond Activation by Vinylidene Gold(I) Complexes: A Concerted Asynchronous or Stepwise Process?" (in en). Chemistry - A European Journal 23 (63): 16097–16103. doi:10.1002/chem.201703815. PMID 28922498. https://onlinelibrary.wiley.com/doi/10.1002/chem.201703815.
- ↑ 19.0 19.1 19.2 Klein, Johannes E. M. N.; Knizia, Gerald; Rzepa, Henry S. (October 2019). "Epoxidation of Alkenes by Peracids: From Textbook Mechanisms to a Quantum Mechanically Derived Curly‐Arrow Depiction" (in en). ChemistryOpen 8 (10): 1244–1250. doi:10.1002/open.201900099. ISSN 2191-1363. PMID 31592408.
- ↑ Nunes dos Santos Comprido, Laura; Klein, Johannes E. M. N.; Knizia, Gerald; Kästner, Johannes; Hashmi, A. Stephen K. (2017-08-10). "On the Accessible Reaction Channels of Vinyl Gold(I) Species: π- and σ-Pathways" (in en). Chemistry - A European Journal 23 (45): 10901–10905. doi:10.1002/chem.201702023. PMID 28593697. https://onlinelibrary.wiley.com/doi/10.1002/chem.201702023.
- ↑ Davis-Gilbert, Zachary W.; Wen, Xuelan; Goodpaster, Jason D.; Tonks, Ian A. (2018-06-13). "Mechanism of Ti-Catalyzed Oxidative Nitrene Transfer in [2 + 2 + 1 Pyrrole Synthesis from Alkynes and Azobenzene"] (in en). Journal of the American Chemical Society 140 (23): 7267–7281. doi:10.1021/jacs.8b03546. ISSN 0002-7863. PMID 29763560.
- ↑ Liu, Liu Leo; Zhou, Jiliang; Cao, Levy L.; Kim, Youngsuk; Stephan, Douglas W. (2019-05-22). "Reversible Intramolecular Cycloaddition of Phosphaalkene to an Arene Ring" (in en). Journal of the American Chemical Society 141 (20): 8083–8087. doi:10.1021/jacs.9b03721. ISSN 0002-7863. PMID 31055918. https://pubs.acs.org/doi/10.1021/jacs.9b03721.
- ↑ 23.0 23.1 Klein, Johannes E. M. N.; Knizia, Gerald (2018-09-10). "cPCET versus HAT: A Direct Theoretical Method for Distinguishing X-H Bond-Activation Mechanisms" (in en). Angewandte Chemie 130 (37): 12089–12093. doi:10.1002/ange.201805511. Bibcode: 2018AngCh.13012089K.
 |
