Engineering:Passive integrator circuit

Circuit 1

Circuit 2

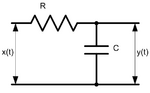
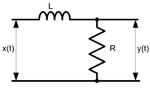
Passive integrator circuit is a simple four-terminal network consisting of two passive elements. It is also the simplest (first-order) low-pass filter.

We'll analyze only the first circuit; the second is very similar.

Transfer function

A transfer ratio is a gain factor for the sinusoidal input signal with given frequency.

A transfer function shows the dependence of the transfer ratio from the signal frequency, given that the input signal is sinusoidal.

According to Ohm's law,

$Y=X\frac{Z_C}{Z_C+Z_R}=X\frac{\frac{1}{j\omega C}}{\frac{1}{j\omega C}+R}=X\frac{1}{1+j\omega RC},$

where $X$ and $Y$ are input and output signals' amplitudes respectively, and $Z_R$ and $Z_C$ are the resistor's and capacitor's impedances.
Therefore, the complex transfer function is

$K(j\omega )=\frac{1}{1+j\omega RC}=\frac{1}{1+\frac{j\omega }{{\omega }_0}},$

where

${\omega }_0=\frac{1}{RC}.$

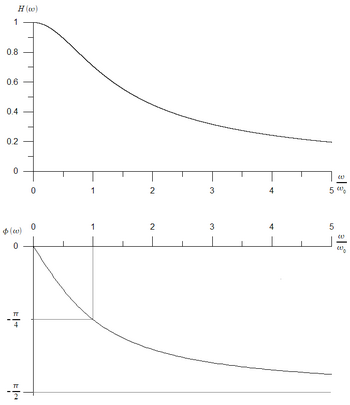
Amplitude transfer function

$H(\omega )=|K(j\omega )|=\frac{1}{\sqrt{1+{\left(\frac{\omega }{{\omega }_0}\right)}^2}}.$

Phase transfer function

$\varphi (\omega )=\arg K(j\omega )=-\arctan \frac{\omega }{{\omega }_0}.$

Amplitude and phase transfer functions for a passive integrator circuit

Transfer functions for the second circuit are the same (with ${\omega }_0=\frac{R}{L}$).

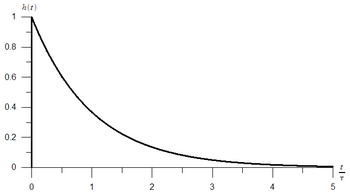
Impulse response

The circuit's Impulse response can be derived as an inverse Laplace transform of the complex transfer function:

$h(t)={{ℒ}}^{-1}\{K(p)\}=\underset{\beta -j\mathrm{\infty }}{\overset{\beta +j\mathrm{\infty }}{\int }}K(p)e^{pt}dp={\omega }_0{e}^{-{\omega }_{0}t}=\frac{1}{\tau }{e}^{-\frac{t}{\tau }},$

where $\tau =\frac{1}{{\omega }_0}$ is a time constant.

An impulse response of a passive integrator circuit

Applications

A passive integrator circuit can serve as a simple integrator. It is also one of the basic electronic circuits, being widely used in circuit analysis based on the equivalent circuit method.

It is often used in cheap digital audio systems (i.e. cheap soundcards) as a reconstruction filter.

See also

• Differentiator
• Electronic filter
• Op amp integrator
• RC circuit