Fat-tailed distribution
A fat-tailed distribution is a probability distribution that exhibits a large skewness or kurtosis, relative to that of either a normal distribution or an exponential distribution.[when defined as?] In common usage, the terms fat-tailed and heavy-tailed are sometimes synonymous; fat-tailed is sometimes also defined as a subset of heavy-tailed. Different research communities favor one or the other largely for historical reasons, and may have differences in the precise definition of either.
Fat-tailed distributions have been empirically encountered in a variety of areas: physics, earth sciences, economics and political science. The class of fat-tailed distributions includes those whose tails decay like a power law, which is a common point of reference in their use in the scientific literature. However, fat-tailed distributions also include other slowly-decaying distributions, such as the log-normal.[1]
The extreme case: a power-law distribution
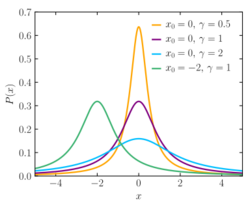
The most extreme case of a fat tail is given by a distribution whose tail decays like a power law.
That is, if the complementary cumulative distribution of a random variable X can be expressed as[citation needed]
- [math]\displaystyle{ \Pr \left\{\ X \gt x\ \right\} \sim x^{- \alpha} \quad }[/math] as [math]\displaystyle{ \quad x \to \infty \quad }[/math] for [math]\displaystyle{ \quad \alpha \gt 0 \; , }[/math]
then the distribution is said to have a fat tail if [math]\displaystyle{ \alpha\lt 2 }[/math]. For such values the variance and the skewness of the tail are mathematically undefined (a special property of the power-law distribution), and hence larger than any normal or exponential distribution. For values of [math]\displaystyle{ \ \alpha \gt 2\ , }[/math] the claim of a fat tail is more ambiguous, because in this parameter range, the variance, skewness, and kurtosis can be finite, depending on the precise value of [math]\displaystyle{ \ \alpha\ , }[/math] and thus potentially smaller than a high-variance normal or exponential tail. This ambiguity often leads to disagreements about precisely what is, or is not, a fat-tailed distribution. For [math]\displaystyle{ \ k \gt \alpha - 1\ , }[/math] the [math]\displaystyle{ \ k^\mathsf{th}\ }[/math] moment is infinite, so for every power law distribution, some moments are undefined.[2]
- Note
- Here the tilde notation "[math]\displaystyle{ \sim }[/math]" means that the tail of the distribution decays like a power law; more technically, it refers to the asymptotic equivalence of functions – meaning that their ratio asymptotically tends to a constant.[citation needed]
Fat tails and risk estimate distortions
Compared to fat-tailed distributions, in the normal distribution, events that deviate from the mean by five or more standard deviations ("5-sigma events") have lower probability, meaning that in the normal distribution extreme events are less likely than for fat-tailed distributions. Fat-tailed distributions such as the Cauchy distribution (and all other stable distributions with the exception of the normal distribution) have "undefined sigma" (more technically, the variance is undefined).
As a consequence, when data arise from an underlying fat-tailed distribution, shoehorning in the "normal distribution" model of risk—and estimating sigma based (necessarily) on a finite sample size—would understate the true degree of predictive difficulty (and of risk). Many—notably Benoît Mandelbrot as well as Nassim Taleb—have noted this shortcoming of the normal distribution model and have proposed that fat-tailed distributions such as the stable distributions govern asset returns frequently found in finance.[3][4][5]
The Black–Scholes model of option pricing is based on a normal distribution. If the distribution is actually a fat-tailed one, then the model will under-price options that are far out of the money, since a 5- or 7-sigma event is much more likely than the normal distribution would predict.[6]
Applications in economics
In finance, fat tails often occur but are considered undesirable because of the additional risk they imply. For example, an investment strategy may have an expected return, after one year, that is five times its standard deviation. Assuming a normal distribution, the likelihood of its failure (negative return) is less than one in a million; in practice, it may be higher. Normal distributions that emerge in finance generally do so because the factors influencing an asset's value or price are mathematically "well-behaved", and the central limit theorem provides for such a distribution. However, traumatic "real-world" events (such as an oil shock, a large corporate bankruptcy, or an abrupt change in a political situation) are usually not mathematically well-behaved.
Historical examples include the Wall Street Crash of 1929, Black Monday (1987), Dot-com bubble, Late-2000s financial crisis, 2010 flash crash, the 2020 stock market crash and the unpegging of some currencies.[7]
Fat tails in market return distributions also have some behavioral origins (investor excessive optimism or pessimism leading to large market moves) and are therefore studied in behavioral finance.
In marketing, the familiar 80-20 rule frequently found (e.g. "20% of customers account for 80% of the revenue") is a manifestation of a fat tail distribution underlying the data.[8]
The "fat tails" are also observed in commodity markets or in the record industry, especially in phonographic markets. The probability density function for logarithm of weekly record sales changes is highly leptokurtic and characterized by a narrower and larger maximum, and by a fatter tail than in the normal distribution case. On the other hand, this distribution has only one fat tail associated with an increase in sales due to promotion of the new records that enter the charts.[9]
See also
References
- ↑ Bahat; Rabinovich; Frid (2005). Tensile Fracturing in Rocks. Springer. https://books.google.com/books?id=A9KumbRohY4C&pg=PA487.
- ↑ Thomas, Mikosch (1999). Regular variation subexponentiality and their applications in probability theory (Report). Workshop Centre in the area of Stochastics, Department of Mathematics and Computer Science. Eindhoven, NL: Eindhoven University of Technology. https://www.eurandom.tue.nl/reports/1999/013-report.pdf.
- ↑ Taleb, N. N. (2007). The Black Swan. Random House and Penguin. ISBN 9781400063512. https://archive.org/details/blackswanimpacto00tale.
- ↑ Mandelbrot, B. (1997). Fractals and Scaling in Finance: Discontinuity, Concentration, Risk. Springer.
- ↑ Mandelbrot, B. (1963). "The Variation of Certain Speculative Prices". The Journal of Business 36 (4): 394. doi:10.1086/294632. http://web.williams.edu/Mathematics/sjmiller/public_html/341Fa09/econ/Mandelbroit_VariationCertainSpeculativePrices.pdf.
- ↑ Steven R. Dunbar, Limitations of the Black-Scholes Model, Stochastic Processes and Advanced Mathematical Finance 2009 http://www.math.unl.edu/~sdunbar1/MathematicalFinance/Lessons/BlackScholes/Limitations/limitations.xml
- ↑ Dash, Jan W. (2004). Quantitative Finance and Risk Management: A Physicist's Approach. World Scientific Pub. https://books.google.com/books?id=jy0WU884hW0C&pg=PA288.
- ↑ Koch, Richard, 1950- (2008). The 80/20 principle : the secret of achieving more with less (Rev. and updated ed.). New York: Doubleday. ISBN 9780385528313. OCLC 429075591.
- ↑ Buda, A. (2012). "Does pop music exist? Hierarchical structure in phonographic markets". Physica A 391 (21): 5153–5159. doi:10.1016/j.physa.2012.05.057.
External links
 |  |
