Log-normal distribution

Short description: Probability distribution

Log-normal

Probability density function 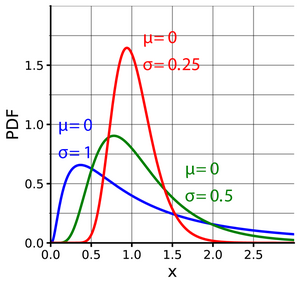Identical parameter [math]\displaystyle{ \ \mu\ }[/math] but differing parameters [math]\displaystyle{ \sigma }[/math]
Cumulative distribution function 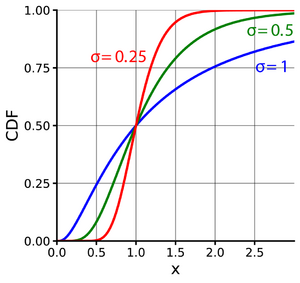[math]\displaystyle{ \ \mu = 0\ }[/math]
Notation	[math]\displaystyle{ \ \operatorname{Lognormal}\left(\ \mu,\,\sigma^2\ \right)\ }[/math]
Parameters	[math]\displaystyle{ \ \mu \in (\ -\infty, +\infty\ )\ }[/math] (logarithm of scale), [math]\displaystyle{ \ \sigma \gt 0\ }[/math]
Support	[math]\displaystyle{ \ x \in (\ 0, +\infty\ )\ }[/math]
PDF	[math]\displaystyle{ \ \frac{ 1 }{\ x\sigma\sqrt{2\pi\ }\ }\ \exp\left( - \frac{ \left( \ln x - \mu\ \right)^2}{ 2 \sigma^2 } \right) }[/math]
CDF	[math]\displaystyle{ \ \frac{\ 1\ }{2}\left[1 + \operatorname{erf}\left( \frac{\ \ln x - \mu\ }{\sigma\sqrt{2\ }} \right)\right] = \Phi\left(\frac{\ln(x) -\mu}{\sigma} \right) }[/math]
Quantile	[math]\displaystyle{ \ \exp\left( \mu + \sqrt{2\sigma^2}\operatorname{erf}^{-1}(2 p - 1) \right)\ }[/math]
Mean	[math]\displaystyle{ \ \exp\left(\ \mu + \frac{\sigma^2}{2}\ \right)\ }[/math]
Median	[math]\displaystyle{ \ \exp(\ \mu\ )\ }[/math]
Mode	[math]\displaystyle{ \ \exp\left(\ \mu - \sigma^2\ \right)\ }[/math]
Variance	[math]\displaystyle{ \ \left[\ \exp(\sigma^2) - 1\ \right]\ \exp\left( 2\ \mu + \sigma^2\right )\ }[/math]
Skewness	[math]\displaystyle{ \ \left[\ \exp\left( \sigma^2 \right) + 2\ \right] \sqrt{\exp(\sigma^2) - 1 \;} }[/math]
Kurtosis	[math]\displaystyle{ \ 1\ \exp\left( 4\ \sigma^2 \right) + 2\ \exp\left( 3\ \sigma^2 \right) + 3\ \exp\left( 2\sigma^2 \right) - 6\ }[/math]
Entropy	[math]\displaystyle{ \ \log_2 \left(\ \sqrt{2\pi\ }\ \sigma\ e^{ \mu + \tfrac{1}{2} }\ \right)\ }[/math]
MGF	defined only for numbers with a  non-positive real part, see text
CF	representation [math]\displaystyle{ \ \sum_{n=0}^{\infty} \frac{\ (i\ t)^n\ }{ n! }e^{\ n \mu + n^2 \sigma^2/2}\ }[/math]  is asymptotically divergent, but adequate  for most numerical purposes
Fisher information	[math]\displaystyle{ \ \begin{pmatrix} \frac{ 1 }{\ \sigma^2\ } & 0 \\ 0 & \frac{2}{\ \sigma^2\ } \end{pmatrix}\ }[/math]

In probability theory, a log-normal (or lognormal) distribution is a continuous probability distribution of a random variable whose logarithm is normally distributed. Thus, if the random variable X is log-normally distributed, then Y = ln(X) has a normal distribution. Equivalently, if Y has a normal distribution, then the exponential function of Y, X = exp(Y) , has a log-normal distribution. A random variable which is log-normally distributed takes only positive real values. It is a convenient and useful model for measurements in exact and engineering sciences, as well as medicine, economics and other topics (e.g., energies, concentrations, lengths, prices of financial instruments, and other metrics).

The distribution is occasionally referred to as the Galton distribution or Galton's distribution, after Francis Galton. The log-normal distribution has also been associated with other names, such as McAlister, Gibrat and Cobb–Douglas.

A log-normal process is the statistical realization of the multiplicative product of many independent random variables, each of which is positive. This is justified by considering the central limit theorem in the log domain (sometimes called Gibrat's law). The log-normal distribution is the maximum entropy probability distribution for a random variate X—for which the mean and variance of ln(X) are specified.

Definitions

Generation and parameters

Let [math]\displaystyle{ \ Z\ }[/math] be a standard normal variable, and let [math]\displaystyle{ \mu }[/math] and [math]\displaystyle{ \sigma }[/math] be two real numbers, with [math]\displaystyle{ \sigma \gt 0 }[/math]. Then, the distribution of the random variable

[math]\displaystyle{ X = e^{\mu + \sigma Z} }[/math]

is called the log-normal distribution with parameters [math]\displaystyle{ \mu }[/math] and [math]\displaystyle{ \sigma }[/math]. These are the expected value (or mean) and standard deviation of the variable's natural logarithm, not the expectation and standard deviation of [math]\displaystyle{ \ X\ }[/math] itself.

Relation between normal and log-normal distribution. If [math]\displaystyle{ \ Y = \mu + \sigma Z\ }[/math] is normally distributed, then [math]\displaystyle{ \ X \sim e^{Y}\ }[/math] is log-normally distributed.

This relationship is true regardless of the base of the logarithmic or exponential function: If [math]\displaystyle{ \ \log_a(X)\ }[/math] is normally distributed, then so is [math]\displaystyle{ \ \log_b(X)\ }[/math] for any two positive numbers [math]\displaystyle{ \ a, b \neq 1 ~. }[/math] Likewise, if [math]\displaystyle{ \ e^Y\ }[/math] is log-normally distributed, then so is [math]\displaystyle{ \ a^Y\ , }[/math] where [math]\displaystyle{ 0 \lt a \neq 1 }[/math].

In order to produce a distribution with desired mean [math]\displaystyle{ \mu_X }[/math] and variance [math]\displaystyle{ \ \sigma_X^2\ , }[/math] one uses [math]\displaystyle{ \ \mu = \ln\left( \frac{ \mu_X^2 }{\ \sqrt{ \mu_X^2 + \sigma_X^2\ }\ }\right)\ }[/math] and [math]\displaystyle{ \ \sigma^2 = \ln\left( 1 + \frac{\ \sigma_X^2\ }{ \mu_X^2 } \right) ~. }[/math]

Alternatively, the "multiplicative" or "geometric" parameters [math]\displaystyle{ \ \mu^* = e^\mu\ }[/math] and [math]\displaystyle{ \ \sigma^* = e^\sigma\ }[/math] can be used. They have a more direct interpretation: [math]\displaystyle{ \ \mu^*\ }[/math] is the median of the distribution, and [math]\displaystyle{ \ \sigma^*\ }[/math] is useful for determining "scatter" intervals, see below.

Probability density function

A positive random variable [math]\displaystyle{ \ X\ }[/math] is log-normally distributed (i.e., [math]\displaystyle{ \ X \sim \operatorname{Lognormal}\left(\ \mu_x, \sigma_x^2\ \right)\ }[/math]), if the natural logarithm of [math]\displaystyle{ \ X\ }[/math] is normally distributed with mean [math]\displaystyle{ \mu }[/math] and variance [math]\displaystyle{ \ \sigma^2\ : }[/math]

[math]\displaystyle{ \ln(X) \sim \mathcal{N}(\mu,\sigma^2) }[/math]

Let [math]\displaystyle{ \ \Phi\ }[/math] and [math]\displaystyle{ \ \varphi\ }[/math] be respectively the cumulative probability distribution function and the probability density function of the [math]\displaystyle{ \ \mathcal{N}(\ 0, 1\ )\ }[/math] standard normal distribution, then we have that the probability density function of the log-normal distribution is given by:

[math]\displaystyle{ \begin{align} f_X(x) & = \frac{ \rm{d} }{ {\rm d} x }\ \operatorname{\mathbb{P}_\mathit{X}}\,\!\bigl[\ X \le x\ \bigr] \\[6pt] & = \frac{ \rm{d} }{ {\rm d} x }\ \operatorname{\mathbb{P}_\mathit{X}}\,\!\bigl[\ \ln X \le \ln x\ \bigr] \\[6pt] & = \frac{ \rm{d} }{ {\rm d} x } \operatorname{\Phi}\!\!\left( \frac{\ \ln x -\mu\ }{ \sigma } \right) \\[6pt] & = \operatorname{\varphi}\!\left( \frac{\ln x - \mu} \sigma \right) \frac{ \rm{d} }{ {\rm d} x } \left( \frac{\ \ln x - \mu\ }{ \sigma }\right) \\[6pt] & = \operatorname{\varphi}\!\left( \frac{\ \ln x - \mu\ }{ \sigma } \right) \frac{ 1 }{\ \sigma\ x\ } \\[6pt] & = \frac{ 1 }{\ x\ \sigma\sqrt{2\ \pi\ }\ } \exp\left( -\frac{\ (\ln x-\mu)^2\ }{2\ \sigma^2} \right) ~. \end{align} }[/math]

Cumulative distribution function

The cumulative distribution function is

[math]\displaystyle{ F_X(x) = \Phi\left( \frac{(\ln x) - \mu} \sigma \right) }[/math]

where [math]\displaystyle{ \ \Phi\ }[/math] is the cumulative distribution function of the standard normal distribution (i.e., [math]\displaystyle{ \ \operatorname\mathcal{N}(\ 0,\ 1 )\ }[/math]).

This may also be expressed as follows:

[math]\displaystyle{ \frac12 \left[ 1 + \operatorname{erf} \left(\frac{\ln x - \mu}{\sigma\sqrt{2}}\right) \right] = \frac12 \operatorname{erfc} \left(-\frac{\ln x - \mu}{\sigma\sqrt{2}}\right) }[/math]

where erfc is the complementary error function.

Multivariate log-normal

If [math]\displaystyle{ \boldsymbol X \sim \mathcal{N}(\boldsymbol\mu,\,\boldsymbol\Sigma) }[/math] is a multivariate normal distribution, then [math]\displaystyle{ Y_i=\exp(X_i) }[/math] has a multivariate log-normal distribution. The exponential is applied elementwise to the random vector [math]\displaystyle{ \boldsymbol X }[/math]. The mean of [math]\displaystyle{ \boldsymbol Y }[/math] is

[math]\displaystyle{ \operatorname{E}[\boldsymbol Y]_i=e^{\mu_i+\frac{1}{2}\Sigma_{ii}} , }[/math]

and its covariance matrix is

[math]\displaystyle{ \operatorname{Var}[\boldsymbol Y]_{ij}=e^{\mu_i+\mu_j + \frac{1}{2}(\Sigma_{ii}+\Sigma_{jj}) }( e^{\Sigma_{ij}} - 1) . }[/math]

Since the multivariate log-normal distribution is not widely used, the rest of this entry only deals with the univariate distribution.

Characteristic function and moment generating function

All moments of the log-normal distribution exist and

[math]\displaystyle{ \operatorname{E}[X^n]= e^{n\mu+n^2\sigma^2/2} }[/math]

This can be derived by letting [math]\displaystyle{ z=\tfrac{\ln(x) - (\mu+n\sigma^2)}{\sigma} }[/math] within the integral. However, the log-normal distribution is not determined by its moments. This implies that it cannot have a defined moment generating function in a neighborhood of zero. Indeed, the expected value [math]\displaystyle{ \operatorname{E}[e^{t X}] }[/math] is not defined for any positive value of the argument [math]\displaystyle{ t }[/math], since the defining integral diverges.

The characteristic function [math]\displaystyle{ \operatorname{E}[e^{i t X}] }[/math] is defined for real values of t, but is not defined for any complex value of t that has a negative imaginary part, and hence the characteristic function is not analytic at the origin. Consequently, the characteristic function of the log-normal distribution cannot be represented as an infinite convergent series. In particular, its Taylor formal series diverges:

[math]\displaystyle{ \sum_{n=0}^\infty \frac{(it)^n}{n!}e^{n\mu+n^2\sigma^2/2} }[/math]

However, a number of alternative divergent series representations have been obtained.

A closed-form formula for the characteristic function [math]\displaystyle{ \varphi(t) }[/math] with [math]\displaystyle{ t }[/math] in the domain of convergence is not known. A relatively simple approximating formula is available in closed form, and is given by

[math]\displaystyle{ \varphi(t)\approx\frac{\exp\left(-\frac{W^2(-it\sigma^2e^\mu) + 2W(-it\sigma^2e^\mu)}{2\sigma^2} \right)}{\sqrt{1+W(-it\sigma^2e^\mu)}} }[/math]

where [math]\displaystyle{ W }[/math] is the Lambert W function. This approximation is derived via an asymptotic method, but it stays sharp all over the domain of convergence of [math]\displaystyle{ \varphi }[/math].

Properties

a. [math]\displaystyle{ y }[/math] is a log-normal variable with [math]\displaystyle{ \mu=1, \sigma=0.5 }[/math]. [math]\displaystyle{ p(\sin y\gt 0) }[/math] is computed by transforming to the normal variable [math]\displaystyle{ x = \ln y }[/math], then integrating its density over the domain defined by [math]\displaystyle{ \sin e^x\gt 0 }[/math] (blue regions), using the numerical method of ray-tracing. b & c. The pdf and cdf of the function [math]\displaystyle{ \sin y }[/math] of the log-normal variable can also be computed in this way.

Probability in different domains

The probability content of a log-normal distribution in any arbitrary domain can be computed to desired precision by first transforming the variable to normal, then numerically integrating using the ray-trace method. (Matlab code)

Probabilities of functions of a log-normal variable

Since the probability of a log-normal can be computed in any domain, this means that the cdf (and consequently pdf and inverse cdf) of any function of a log-normal variable can also be computed. (Matlab code)

Geometric or multiplicative moments

The geometric or multiplicative mean of the log-normal distribution is [math]\displaystyle{ \operatorname{GM}[X] = e^\mu = \mu^* }[/math]. It equals the median. The geometric or multiplicative standard deviation is [math]\displaystyle{ \operatorname{GSD}[X] = e^{\sigma} = \sigma^* }[/math].

By analogy with the arithmetic statistics, one can define a geometric variance, [math]\displaystyle{ \operatorname{GVar}[X] = e^{\sigma^2} }[/math], and a geometric coefficient of variation, [math]\displaystyle{ \operatorname{GCV}[X] = e^{\sigma} - 1 }[/math], has been proposed. This term was intended to be analogous to the coefficient of variation, for describing multiplicative variation in log-normal data, but this definition of GCV has no theoretical basis as an estimate of [math]\displaystyle{ \operatorname{CV} }[/math] itself (see also Coefficient of variation).

Note that the geometric mean is smaller than the arithmetic mean. This is due to the AM–GM inequality and is a consequence of the logarithm being a concave function. In fact,

[math]\displaystyle{ \operatorname{E}[X] = e^{\mu + \frac12 \sigma^2} = e^{\mu} \cdot \sqrt{e^{\sigma^2}} = \operatorname{GM}[X] \cdot \sqrt{\operatorname{GVar}[X]}. }[/math]

In finance, the term [math]\displaystyle{ e^{-\frac12\sigma^2} }[/math] is sometimes interpreted as a convexity correction. From the point of view of stochastic calculus, this is the same correction term as in Itō's lemma for geometric Brownian motion.

Arithmetic moments

For any real or complex number n, the n-th moment of a log-normally distributed variable X is given by

[math]\displaystyle{ \operatorname{E}[X^n] = e^{n\mu + \frac12n^2\sigma^2}. }[/math]

Specifically, the arithmetic mean, expected square, arithmetic variance, and arithmetic standard deviation of a log-normally distributed variable X are respectively given by:

[math]\displaystyle{ \begin{align} \operatorname{E}[X] & = e^{\mu + \tfrac{1}{2}\sigma^2}, \\[4pt] \operatorname{E}[X^2] & = e^{2\mu + 2\sigma^2}, \\[4pt] \operatorname{Var}[X] & = \operatorname{E}[X^2] - \operatorname{E}[X]^2 = (\operatorname{E}[X])^2(e^{\sigma^2} - 1) = e^{2\mu + \sigma^2} (e^{\sigma^2} - 1), \\[4pt] \operatorname{SD}[X] & = \sqrt{\operatorname{Var}[X]} = \operatorname{E}[X] \sqrt{e^{\sigma^2} - 1} = e^{\mu + \tfrac{1}{2}\sigma^2}\sqrt{e^{\sigma^2} - 1}, \end{align} }[/math]

The arithmetic coefficient of variation [math]\displaystyle{ \operatorname{CV}[X] }[/math] is the ratio [math]\displaystyle{ \tfrac{\operatorname{SD}[X]}{\operatorname{E}[X]} }[/math]. For a log-normal distribution it is equal to

[math]\displaystyle{ \operatorname{CV}[X] = \sqrt{e^{\sigma^2} - 1}. }[/math]

This estimate is sometimes referred to as the "geometric CV" (GCV), due to its use of the geometric variance. Contrary to the arithmetic standard deviation, the arithmetic coefficient of variation is independent of the arithmetic mean.

The parameters μ and σ can be obtained, if the arithmetic mean and the arithmetic variance are known:

[math]\displaystyle{ \begin{align} \mu &= \ln \left(\frac{\operatorname{E}[X]^2}{\sqrt{\operatorname{E}[X^2]}}\right) = \ln \left( \frac{\operatorname{E}[X]^2}{\sqrt{\operatorname{Var}[X] + \operatorname{E}[X]^2}} \right), \\[4pt] \sigma^2 &= \ln \left(\frac{\operatorname{E}[X^2]}{\operatorname{E}[X]^2}\right) = \ln \left(1 + \frac{\operatorname{Var}[X]}{\operatorname{E}[X]^2}\right). \end{align} }[/math]

A probability distribution is not uniquely determined by the moments E[Xⁿ] = e^{nμ + 1/2n2σ2} for n ≥ 1. That is, there exist other distributions with the same set of moments. In fact, there is a whole family of distributions with the same moments as the log-normal distribution.

Mode, median, quantiles

Comparison of mean, median and mode of two log-normal distributions with different skewness.

The mode is the point of global maximum of the probability density function. In particular, by solving the equation [math]\displaystyle{ (\ln f)'=0 }[/math], we get that:

[math]\displaystyle{ \operatorname{Mode}[X] = e^{\mu - \sigma^2}. }[/math]

Since the log-transformed variable [math]\displaystyle{ Y = \ln X }[/math] has a normal distribution, and quantiles are preserved under monotonic transformations, the quantiles of [math]\displaystyle{ X }[/math] are

[math]\displaystyle{ q_X(\alpha) = e^{\mu+\sigma q_\Phi(\alpha)} =\mu^* (\sigma^*)^{q_\Phi(\alpha)}, }[/math]

where [math]\displaystyle{ q_\Phi(\alpha) }[/math] is the quantile of the standard normal distribution.

Specifically, the median of a log-normal distribution is equal to its multiplicative mean,

[math]\displaystyle{ \operatorname{Med}[X] = e^\mu = \mu^* ~. }[/math]

Partial expectation

The partial expectation of a random variable [math]\displaystyle{ X }[/math] with respect to a threshold [math]\displaystyle{ k }[/math] is defined as

[math]\displaystyle{ g(k) = \int_k^\infty x f_X(x \mid X \gt k)\, dx . }[/math]

Alternatively, by using the definition of conditional expectation, it can be written as [math]\displaystyle{ g(k)=\operatorname{E}[X\mid X\gt k] P(X\gt k) }[/math]. For a log-normal random variable, the partial expectation is given by:

[math]\displaystyle{ g(k) = \int_k^\infty x f_X(x \mid X \gt k)\, dx = e^{\mu+\tfrac{1}{2} \sigma^2}\, \Phi\!\left(\frac{\mu+\sigma^2-\ln k} \sigma \right) }[/math]

where [math]\displaystyle{ \Phi }[/math] is the normal cumulative distribution function. The derivation of the formula is provided in the Talk page. The partial expectation formula has applications in insurance and economics, it is used in solving the partial differential equation leading to the Black–Scholes formula.

Conditional expectation

The conditional expectation of a log-normal random variable [math]\displaystyle{ X }[/math]—with respect to a threshold [math]\displaystyle{ k }[/math]—is its partial expectation divided by the cumulative probability of being in that range:

[math]\displaystyle{ \begin{align} E[X\mid X\lt k] & =e^{\mu +\frac{\sigma^2}{2}}\cdot \frac{\Phi \left[\frac{\ln(k)-\mu -\sigma^2}{\sigma} \right]}{\Phi \left[\frac{\ln(k)-\mu}{\sigma} \right]} \\[8pt] E[X\mid X\geqslant k] &=e^{\mu +\frac{\sigma^2}{2}}\cdot \frac{\Phi \left[\frac{\mu +\sigma^2-\ln(k)} \sigma \right]}{1-\Phi \left[\frac{\ln(k)-\mu}{\sigma}\right]} \\ [8pt] E[X\mid X\in [k_1,k_2]] &=e^{\mu +\frac{\sigma^2}{2}}\cdot \frac{ \Phi \left[\frac{\ln(k_2)-\mu -\sigma^2} \sigma \right]-\Phi \left[\frac{\ln(k_1)-\mu -\sigma^2} \sigma \right] }{ \Phi \left[\frac{\ln(k_2)-\mu}{\sigma}\right]-\Phi \left[\frac{\ln(k_1)-\mu}{\sigma}\right] } \end{align} }[/math]

Alternative parameterizations

In addition to the characterization by [math]\displaystyle{ \mu, \sigma }[/math] or [math]\displaystyle{ \mu^*, \sigma^* }[/math], here are multiple ways how the log-normal distribution can be parameterized. ProbOnto, the knowledge base and ontology of probability distributions lists seven such forms:

Overview of parameterizations of the log-normal distributions.

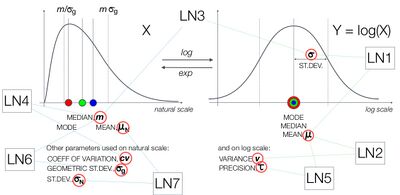
• LogNormal1(μ,σ) with mean, μ, and standard deviation, σ, both on the log-scale

  [math]\displaystyle{ P(x;\boldsymbol\mu,\boldsymbol\sigma)=\frac{1}{x \sigma \sqrt{2 \pi}} \exp\left[-\frac{(\ln x - \mu)^2}{2 \sigma^2}\right] }[/math]

• LogNormal2(μ,υ) with mean, μ, and variance, υ, both on the log-scale

  [math]\displaystyle{ P(x;\boldsymbol\mu,\boldsymbol {v})=\frac{1}{x \sqrt{v} \sqrt{2 \pi}} \exp\left[-\frac{(\ln x - \mu)^2}{2 v}\right] }[/math]

• LogNormal3(m,σ) with median, m, on the natural scale and standard deviation, σ, on the log-scale

  [math]\displaystyle{ P(x;\boldsymbol m,\boldsymbol \sigma) =\frac{1}{x \sigma \sqrt{2 \pi}} \exp\left[-\frac{\ln^2(x/m)}{2 \sigma^2}\right] }[/math]

• LogNormal4(m,cv) with median, m, and coefficient of variation, cv, both on the natural scale

  [math]\displaystyle{ P(x;\boldsymbol m,\boldsymbol {cv})= \frac{1}{x \sqrt{\ln(cv^2+1)} \sqrt{2 \pi}} \exp\left[-\frac{\ln^2(x/m)}{2\ln(cv^2+1)}\right] }[/math]

• LogNormal5(μ,τ) with mean, μ, and precision, τ, both on the log-scale

  [math]\displaystyle{ P(x;\boldsymbol\mu,\boldsymbol \tau)=\sqrt{\frac{\tau}{2 \pi}} \frac{1}{x} \exp\left[-\frac{\tau}{2}(\ln x-\mu)^2\right] }[/math]

• LogNormal6(m,σ_g) with median, m, and geometric standard deviation, σ_g, both on the natural scale

  [math]\displaystyle{ P(x;\boldsymbol m,\boldsymbol {\sigma_g})=\frac{1}{x \ln(\sigma_g)\sqrt{2 \pi}} \exp\left[-\frac{\ln^2(x/m)}{2 \ln^2(\sigma_g)}\right] }[/math]

• LogNormal7(μ_N,σ_N) with mean, μ_N, and standard deviation, σ_N, both on the natural scale

  [math]\displaystyle{ P(x;\boldsymbol {\mu_N},\boldsymbol {\sigma_N})= \frac{1}{x \sqrt{2 \pi \ln\left(1+\sigma_N^2/\mu_N^2\right)}} \exp\left(-\frac{\Big[ \ln x - \ln\frac{\mu_N}{\sqrt{1+\sigma_N^2/\mu_N^2}}\Big]^2}{2\ln(1+\sigma_N^2/\mu_N^2)}\right) }[/math]

Examples for re-parameterization

Consider the situation when one would like to run a model using two different optimal design tools, for example PFIM and PopED. The former supports the LN2, the latter LN7 parameterization, respectively. Therefore, the re-parameterization is required, otherwise the two tools would produce different results.

For the transition [math]\displaystyle{ \operatorname{LN2}(\mu, v) \to \operatorname{LN7}(\mu_N, \sigma_N) }[/math] following formulas hold [math]\displaystyle{ \mu_N = \exp(\mu+v/2) }[/math] and [math]\displaystyle{ \sigma_N = \exp(\mu+v/2)\sqrt{\exp(v)-1} }[/math].

For the transition [math]\displaystyle{ \operatorname{LN7}(\mu_N, \sigma_N) \to \operatorname{LN2}(\mu, v) }[/math] following formulas hold [math]\displaystyle{ \mu = \ln\left( \mu_N / \sqrt{1+\sigma_N^2/\mu_N^2} \right) }[/math] and [math]\displaystyle{ v = \ln(1+\sigma_N^2/\mu_N^2) }[/math].

All remaining re-parameterisation formulas can be found in the specification document on the project website.

Multiple, reciprocal, power

• Multiplication by a constant: If [math]\displaystyle{ X \sim \operatorname{Lognormal}(\mu, \sigma^2) }[/math] then [math]\displaystyle{ a X \sim \operatorname{Lognormal}( \mu + \ln a,\ \sigma^2) }[/math] for [math]\displaystyle{ a \gt 0. }[/math]
• Reciprocal: If [math]\displaystyle{ X \sim \operatorname{Lognormal}(\mu, \sigma^2) }[/math] then [math]\displaystyle{ \tfrac{1}{X} \sim \operatorname{Lognormal}(-\mu,\ \sigma^2). }[/math]
• Power: If [math]\displaystyle{ X \sim \operatorname{Lognormal}(\mu, \sigma^2) }[/math] then [math]\displaystyle{ X^a \sim \operatorname{Lognormal}(a\mu,\ a^2 \sigma^2) }[/math] for [math]\displaystyle{ a \neq 0. }[/math]

Multiplication and division of independent, log-normal random variables

If two independent, log-normal variables [math]\displaystyle{ X_1 }[/math] and [math]\displaystyle{ X_2 }[/math] are multiplied [divided], the product [ratio] is again log-normal, with parameters [math]\displaystyle{ \mu=\mu_1+\mu_2 }[/math] [[math]\displaystyle{ \mu=\mu_1-\mu_2 }[/math]] and [math]\displaystyle{ \sigma }[/math], where [math]\displaystyle{ \sigma^2=\sigma_1^2+\sigma_2^2 }[/math]. This is easily generalized to the product of [math]\displaystyle{ n }[/math] such variables.

More generally, if [math]\displaystyle{ X_j \sim \operatorname{Lognormal} (\mu_j, \sigma_j^2) }[/math] are [math]\displaystyle{ n }[/math] independent, log-normally distributed variables, then [math]\displaystyle{ Y = \textstyle\prod_{j=1}^n X_j \sim \operatorname{Lognormal} \Big(\textstyle \sum_{j=1}^n\mu_j,\ \sum_{j=1}^n \sigma_j^2 \Big). }[/math]

Multiplicative central limit theorem

The geometric or multiplicative mean of [math]\displaystyle{ n }[/math] independent, identically distributed, positive random variables [math]\displaystyle{ X_i }[/math] shows, for [math]\displaystyle{ n \to\infty }[/math] approximately a log-normal distribution with parameters [math]\displaystyle{ \mu = E[\ln(X_i)] }[/math] and [math]\displaystyle{ \sigma^2 = \mbox{var}[\ln(X_i)]/n }[/math], assuming [math]\displaystyle{ \sigma^2 }[/math] is finite.

In fact, the random variables do not have to be identically distributed. It is enough for the distributions of [math]\displaystyle{ \ln(X_i) }[/math] to all have finite variance and satisfy the other conditions of any of the many variants of the central limit theorem.

This is commonly known as Gibrat's law.

Other

A set of data that arises from the log-normal distribution has a symmetric Lorenz curve (see also Lorenz asymmetry coefficient).

The harmonic [math]\displaystyle{ H }[/math], geometric [math]\displaystyle{ G }[/math] and arithmetic [math]\displaystyle{ A }[/math] means of this distribution are related; such relation is given by

[math]\displaystyle{ H = \frac{G^2} A. }[/math]

Log-normal distributions are infinitely divisible, but they are not stable distributions, which can be easily drawn from.

Related distributions

• If [math]\displaystyle{ X \sim \mathcal{N}(\mu, \sigma^2) }[/math] is a normal distribution, then [math]\displaystyle{ \exp(X) \sim \operatorname{Lognormal}(\mu, \sigma^2). }[/math]
• If [math]\displaystyle{ X \sim \operatorname{Lognormal}(\mu, \sigma^2) }[/math] is distributed log-normally, then [math]\displaystyle{ \ln(X) \sim \mathcal{N}(\mu, \sigma^2) }[/math] is a normal random variable.
• Let [math]\displaystyle{ X_j \sim \operatorname{Lognormal}(\mu_j, \sigma_j^2) }[/math] be independent log-normally distributed variables with possibly varying [math]\displaystyle{ \sigma }[/math] and [math]\displaystyle{ \mu }[/math] parameters, and [math]\displaystyle{ Y = \sum_{j=1}^n X_j }[/math]. The distribution of [math]\displaystyle{ Y }[/math] has no closed-form expression, but can be reasonably approximated by another log-normal distribution [math]\displaystyle{ Z }[/math] at the right tail. Its probability density function at the neighborhood of 0 has been characterized and it does not resemble any log-normal distribution. A commonly used approximation due to L.F. Fenton (but previously stated by R.I. Wilkinson and mathematically justified by Marlow) is obtained by matching the mean and variance of another log-normal distribution: [math]\displaystyle{ \begin{align} \sigma^2_Z &= \ln\!\left[ \frac{\sum e^{2\mu_j+\sigma_j^2}(e^{\sigma_j^2}-1)}{(\sum e^{\mu_j+\sigma_j^2/2})^2} + 1\right], \\ \mu_Z &= \ln\!\left[ \sum e^{\mu_j+\sigma_j^2/2} \right] - \frac{\sigma^2_Z}{2}. \end{align} }[/math] In the case that all [math]\displaystyle{ X_j }[/math] have the same variance parameter [math]\displaystyle{ \sigma_j=\sigma }[/math], these formulas simplify to [math]\displaystyle{ \begin{align} \sigma^2_Z &= \ln\!\left[ (e^{\sigma^2}-1)\frac{\sum e^{2\mu_j}}{(\sum e^{\mu_j})^2} + 1\right], \\ \mu_Z &= \ln\!\left[ \sum e^{\mu_j} \right] + \frac{\sigma^2}{2} - \frac{\sigma^2_Z}{2}. \end{align} }[/math]

For a more accurate approximation, one can use the Monte Carlo method to estimate the cumulative distribution function, the pdf and the right tail.

The sum of correlated log-normally distributed random variables can also be approximated by a log-normal distribution [math]\displaystyle{ \begin{align} S_+ &= \operatorname{E}\left[\sum_i X_i \right] = \sum_i \operatorname{E}[X_i] = \sum_i e^{\mu_i + \sigma_i^2/2} \\ \sigma^2_{Z} &= 1/S_+^2 \, \sum_{i,j} \operatorname{cor}_{ij} \sigma_i \sigma_j \operatorname{E}[X_i] \operatorname{E}[X_j] = 1/S_+^2 \, \sum_{i,j} \operatorname{cor}_{ij} \sigma_i \sigma_j e^{\mu_i+\sigma_i^2/2} e^{\mu_j+\sigma_j^2/2} \\ \mu_Z &= \ln\left( S_+ \right) - \sigma_{Z}^2/2 \end{align} }[/math]

• If [math]\displaystyle{ X \sim \operatorname{Lognormal}(\mu, \sigma^2) }[/math] then [math]\displaystyle{ X+c }[/math] is said to have a Three-parameter log-normal distribution with support [math]\displaystyle{ x\in (c, +\infty) }[/math]. [math]\displaystyle{ \operatorname{E}[X+c] = \operatorname{E}[X] + c }[/math], [math]\displaystyle{ \operatorname{Var}[X+c] = \operatorname{Var}[X] }[/math].
• The log-normal distribution is a special case of the semi-bounded Johnson's SU-distribution.
• If [math]\displaystyle{ X\mid Y \sim \operatorname{Rayleigh}(Y) }[/math] with [math]\displaystyle{ Y \sim \operatorname{Lognormal}(\mu, \sigma^2) }[/math], then [math]\displaystyle{ X \sim \operatorname{Suzuki}(\mu, \sigma) }[/math] (Suzuki distribution).
• A substitute for the log-normal whose integral can be expressed in terms of more elementary functions can be obtained based on the logistic distribution to get an approximation for the CDF [math]\displaystyle{ F(x;\mu,\sigma) = \left[\left(\frac{e^\mu}{x}\right)^{\pi/(\sigma \sqrt{3})} + 1\right]^{-1}. }[/math] This is a log-logistic distribution.

Statistical inference

Estimation of parameters

For determining the maximum likelihood estimators of the log-normal distribution parameters μ and σ, we can use the same procedure as for the normal distribution. Note that [math]\displaystyle{ L(\mu, \sigma) = \prod_{i=1}^n \frac 1 {x_i} \varphi_{\mu,\sigma} (\ln x_i), }[/math] where [math]\displaystyle{ \varphi }[/math] is the density function of the normal distribution [math]\displaystyle{ \mathcal N(\mu,\sigma^2) }[/math]. Therefore, the log-likelihood function is [math]\displaystyle{ \ell (\mu,\sigma \mid x_1, x_2, \ldots, x_n) = - \sum _i \ln x_i + \ell_N (\mu, \sigma \mid \ln x_1, \ln x_2, \dots, \ln x_n). }[/math]

Since the first term is constant with regard to μ and σ, both logarithmic likelihood functions, [math]\displaystyle{ \ell }[/math] and [math]\displaystyle{ \ell_N }[/math], reach their maximum with the same [math]\displaystyle{ \mu }[/math] and [math]\displaystyle{ \sigma }[/math]. Hence, the maximum likelihood estimators are identical to those for a normal distribution for the observations [math]\displaystyle{ \ln x_1, \ln x_2, \dots, \ln x_n) }[/math], [math]\displaystyle{ \widehat \mu = \frac {\sum_i \ln x_i}{n}, \qquad \widehat \sigma^2 = \frac {\sum_i \left( \ln x_i - \widehat \mu \right)^2} {n}. }[/math]

For finite n, the estimator for [math]\displaystyle{ \mu }[/math] is unbiased, but the one for [math]\displaystyle{ \sigma }[/math] is biased. As for the normal distribution, an unbiased estimator for [math]\displaystyle{ \sigma }[/math] can be obtained by replacing the denominator n by n−1 in the equation for [math]\displaystyle{ \widehat\sigma^2 }[/math].

When the individual values [math]\displaystyle{ x_1, x_2, \ldots, x_n }[/math] are not available, but the sample's mean [math]\displaystyle{ \bar x }[/math] and standard deviation s is, then the Method of moments can be used. The corresponding parameters are determined by the following formulas, obtained from solving the equations for the expectation [math]\displaystyle{ \operatorname{E}[X] }[/math] and variance [math]\displaystyle{ \operatorname{Var}[X] }[/math] for [math]\displaystyle{ \mu }[/math] and [math]\displaystyle{ \sigma }[/math]: [math]\displaystyle{ \mu = \ln\left(\frac{ \bar x} {\sqrt{1+\widehat\sigma^2/\bar x^2} } \right), \qquad \sigma^2 = \ln\left(1 + {\widehat\sigma^2} / \bar x^2 \right). }[/math]

Interval estimates

The most efficient way to obtain interval estimates when analyzing log-normally distributed data consists of applying the well-known methods based on the normal distribution to logarithmically transformed data and then to back-transform results if appropriate.

Prediction intervals

A basic example is given by prediction intervals: For the normal distribution, the interval [math]\displaystyle{ [\mu-\sigma,\mu+\sigma] }[/math] contains approximately two thirds (68%) of the probability (or of a large sample), and [math]\displaystyle{ [\mu-2\sigma,\mu+2\sigma] }[/math] contain 95%. Therefore, for a log-normal distribution, [math]\displaystyle{ [\mu^*/\sigma^*,\mu^*\cdot\sigma^*]=[\mu^* {}^\times\!\!/ \sigma^*] }[/math] contains 2/3, and [math]\displaystyle{ [\mu^*/(\sigma^*)^2,\mu^*\cdot(\sigma^*)^2] = [\mu^* {}^\times\!\!/ (\sigma^*)^2] }[/math] contains 95% of the probability. Using estimated parameters, then approximately the same percentages of the data should be contained in these intervals.

Confidence interval for μ^*

Using the principle, note that a confidence interval for [math]\displaystyle{ \mu }[/math] is [math]\displaystyle{ [\widehat\mu \pm q \cdot \widehat\mathop{se}] }[/math], where [math]\displaystyle{ \mathop{se} = \widehat\sigma / \sqrt{n} }[/math] is the standard error and q is the 97.5% quantile of a t distribution with n-1 degrees of freedom. Back-transformation leads to a confidence interval for [math]\displaystyle{ \mu^* }[/math], [math]\displaystyle{ [\widehat\mu^* {}^\times\!\!/ (\operatorname{sem}^*)^q] }[/math] with [math]\displaystyle{ \operatorname{sem}^*=(\widehat\sigma^*)^{1/\sqrt{n}} }[/math]

Extremal principle of entropy to fix the free parameter σ

In applications, [math]\displaystyle{ \sigma }[/math] is a parameter to be determined. For growing processes balanced by production and dissipation, the use of an extremal principle of Shannon entropy shows that [math]\displaystyle{ \sigma = \frac 1 \sqrt{6} }[/math]

This value can then be used to give some scaling relation between the inflexion point and maximum point of the log-normal distribution. This relationship is determined by the base of natural logarithm, [math]\displaystyle{ e = 2.718\ldots }[/math], and exhibits some geometrical similarity to the minimal surface energy principle. These scaling relations are useful for predicting a number of growth processes (epidemic spreading, droplet splashing, population growth, swirling rate of the bathtub vortex, distribution of language characters, velocity profile of turbulences, etc.). For example, the log-normal function with such [math]\displaystyle{ \sigma }[/math] fits well with the size of secondarily produced droplets during droplet impact and the spreading of an epidemic disease.

The value [math]\displaystyle{ \sigma = 1 \big/ \sqrt{6} }[/math] is used to provide a probabilistic solution for the Drake equation.

Occurrence and applications

The log-normal distribution is important in the description of natural phenomena. Many natural growth processes are driven by the accumulation of many small percentage changes which become additive on a log scale. Under appropriate regularity conditions, the distribution of the resulting accumulated changes will be increasingly well approximated by a log-normal, as noted in the section above on "Multiplicative Central Limit Theorem". This is also known as Gibrat's law, after Robert Gibrat (1904–1980) who formulated it for companies. If the rate of accumulation of these small changes does not vary over time, growth becomes independent of size. Even if this assumption is not true, the size distributions at any age of things that grow over time tends to be log-normal. Consequently, reference ranges for measurements in healthy individuals are more accurately estimated by assuming a log-normal distribution than by assuming a symmetric distribution about the mean.

A second justification is based on the observation that fundamental natural laws imply multiplications and divisions of positive variables. Examples are the simple gravitation law connecting masses and distance with the resulting force, or the formula for equilibrium concentrations of chemicals in a solution that connects concentrations of educts and products. Assuming log-normal distributions of the variables involved leads to consistent models in these cases.

Specific examples are given in the following subsections. contains a review and table of log-normal distributions from geology, biology, medicine, food, ecology, and other areas. is a review article on log-normal distributions in neuroscience, with annotated bibliography.

Human behavior

• The length of comments posted in Internet discussion forums follows a log-normal distribution.
• Users' dwell time on online articles (jokes, news etc.) follows a log-normal distribution.
• The length of chess games tends to follow a log-normal distribution.
• Onset durations of acoustic comparison stimuli that are matched to a standard stimulus follow a log-normal distribution.

Biology and medicine

• Measures of size of living tissue (length, skin area, weight).
• Incubation period of diseases.
• Diameters of banana leaf spots, powdery mildew on barley.
• For highly communicable epidemics, such as SARS in 2003, if public intervention control policies are involved, the number of hospitalized cases is shown to satisfy the log-normal distribution with no free parameters if an entropy is assumed and the standard deviation is determined by the principle of maximum rate of entropy production.
• The length of inert appendages (hair, claws, nails, teeth) of biological specimens, in the direction of growth.
• The normalised RNA-Seq readcount for any genomic region can be well approximated by log-normal distribution.
• The PacBio sequencing read length follows a log-normal distribution.
• Certain physiological measurements, such as blood pressure of adult humans (after separation on male/female subpopulations).
• Several pharmacokinetic variables, such as C_max, elimination half-life and the elimination rate constant.
• In neuroscience, the distribution of firing rates across a population of neurons is often approximately log-normal. This has been first observed in the cortex and striatum and later in hippocampus and entorhinal cortex, and elsewhere in the brain. Also, intrinsic gain distributions and synaptic weight distributions appear to be log-normal as well.
• Neuron densities in the cerebral cortex, due to the noisy cell division process during neurodevelopment.
• In operating-rooms management, the distribution of surgery duration.
• In the size of avalanches of fractures in the cytoskeleton of living cells, showing log-normal distributions, with significantly higher size in cancer cells than healthy ones.

Chemistry

• Particle size distributions and molar mass distributions.
• The concentration of rare elements in minerals.
• Diameters of crystals in ice cream, oil drops in mayonnaise, pores in cocoa press cake.

File:FitLogNormDistr.tif

Hydrology

• In hydrology, the log-normal distribution is used to analyze extreme values of such variables as monthly and annual maximum values of daily rainfall and river discharge volumes.

The image on the right, made with CumFreq, illustrates an example of fitting the log-normal distribution to ranked annually maximum one-day rainfalls showing also the 90% confidence belt based on the binomial distribution.

The rainfall data are represented by plotting positions as part of a cumulative frequency analysis.

Social sciences and demographics

• In economics, there is evidence that the income of 97%–99% of the population is distributed log-normally. (The distribution of higher-income individuals follows a Pareto distribution).
• If an income distribution follows a log-normal distribution with standard deviation [math]\displaystyle{ \sigma }[/math], then the Gini coefficient, commonly use to evaluate income inequality, can be computed as [math]\displaystyle{ G = \operatorname{erf}\left(\frac{\sigma }{2 }\right) }[/math] where [math]\displaystyle{ \operatorname{erf} }[/math] is the error function, since [math]\displaystyle{ G=2 \Phi \left(\frac{\sigma }{\sqrt{2}}\right)-1 }[/math], where [math]\displaystyle{ \Phi(x) }[/math] is the cumulative distribution function of a standard normal distribution.
• In finance, in particular the Black–Scholes model, changes in the logarithm of exchange rates, price indices, and stock market indices are assumed normal (these variables behave like compound interest, not like simple interest, and so are multiplicative). However, some mathematicians such as Benoit Mandelbrot have argued that log-Lévy distributions, which possesses heavy tails would be a more appropriate model, in particular for the analysis for stock market crashes. Indeed, stock price distributions typically exhibit a fat tail. The fat tailed distribution of changes during stock market crashes invalidate the assumptions of the central limit theorem.
• In scientometrics, the number of citations to journal articles and patents follows a discrete log-normal distribution.
• City sizes (population) satisfy Gibrat's Law. The growth process of city sizes is proportionate and invariant with respect to size. From the central limit theorem therefore, the log of city size is normally distributed.
• The number of sexual partners appears to be best described by a log-normal distribution.

Technology

• In reliability analysis, the log-normal distribution is often used to model times to repair a maintainable system.
• In wireless communication, "the local-mean power expressed in logarithmic values, such as dB or neper, has a normal (i.e., Gaussian) distribution." Also, the random obstruction of radio signals due to large buildings and hills, called shadowing, is often modeled as a log-normal distribution.
• Particle size distributions produced by comminution with random impacts, such as in ball milling.
• The file size distribution of publicly available audio and video data files (MIME types) follows a log-normal distribution over five orders of magnitude.
• File sizes of 140 million files on personal computers running the Windows OS, collected in 1999.
• Sizes of text-based emails (1990s) and multimedia-based emails (2000s).
• In computer networks and Internet traffic analysis, log-normal is shown as a good statistical model to represent the amount of traffic per unit time. This has been shown by applying a robust statistical approach on a large groups of real Internet traces. In this context, the log-normal distribution has shown a good performance in two main use cases: (1) predicting the proportion of time traffic will exceed a given level (for service level agreement or link capacity estimation) i.e. link dimensioning based on bandwidth provisioning and (2) predicting 95th percentile pricing.
• in physical testing when the test produces a time-to-failure of an item under specified conditions, the data is often best analyzed using a lognormal distribution.

See also

• Heavy-tailed distribution
• Log-distance path loss model
• Modified lognormal power-law distribution
• Slow fading

Further reading

• Crow, Edwin L., ed. (1988), Lognormal Distributions, Theory and Applications, Statistics: Textbooks and Monographs, 88, New York: Marcel Dekker, Inc., pp. xvi+387, ISBN 978-0-8247-7803-3 
• Aitchison, J. and Brown, J.A.C. (1957) The Lognormal Distribution, Cambridge University Press.
• Limpert, E; Stahel, W; Abbt, M (2001). "Lognormal distributions across the sciences: keys and clues". BioScience 51 (5): 341–352. doi:10.1641/0006-3568(2001)051[0341:LNDATS2.0.CO;2]. 
• Holgate, P. (1989). "The lognormal characteristic function". Communications in Statistics - Theory and Methods 18 (12): 4539–4548. doi:10.1080/03610928908830173. 
• Brooks, Robert; Corson, Jon; Donal, Wales (1994). "The Pricing of Index Options When the Underlying Assets All Follow a Lognormal Diffusion". Advances in Futures and Options Research 7. 

External links

• The normal distribution is the log-normal distribution