Fiber bundle construction theorem

Short description: Constructs a fiber bundle from a base space, fiber and a set of transition functions

The Möbius strip can be constructed by a non-trivial gluing of two trivial bundles on open subsets U and V of the circle S¹. When glued trivially (with g_UV=1) one obtains the trivial bundle, but with the non-trivial gluing of g_UV=1 on one overlap and g_UV=-1 on the second overlap, one obtains the non-trivial bundle E, the Möbius strip. This can be visualised as a "twisting" of one of the local charts.

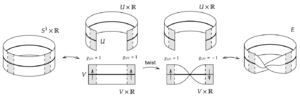
In mathematics, the fiber bundle construction theorem is a theorem which constructs a fiber bundles with a structure group from a given base space, fiber, group, and a suitable set of transition functions. The theorem also gives conditions under which two such bundles are isomorphic.

The theorem is used in the associated bundle construction, where one starts with a given bundle and changes just the fiber, while keeping all other data the same.

Formal statement

Existence

Let X and F be topological spaces and let G be a topological group with a continuous left action on F. Given an open cover {U_i} of X and a set of continuous functions

$t_{ij}:U_i\cap U_j\to G$

defined on each nonempty overlap, such that the cocycle condition

$t_{ik}(x)=t_{ij}(x)t_{jk}(x)\mathrm{\forall }x\in U_i\cap U_j\cap U_k$

holds, there exists a fiber bundle E → X with fiber F and structure group G that is trivializable over {U_i} with transition functions t_ij.

Isomorphism

Let E′ be another fiber bundle with the same base space, fiber, structure group, and trivializing neighborhoods, but transition functions t′_ij. If the action of G on F is faithful, then E′ and E are isomorphic if and only if there exist functions

$t_i:U_i\to G$

such that

$t{\text{'}}_{ij}(x)=t_i(x{)}^{-1}{t}_{ij}(x)t_j(x)\mathrm{\forall }x\in U_i\cap U_j.$

i.e. a gauge transformation on transition data.

In particular, given a base, fiber, structure group, group action on the fiber, trivializing neighborhoods, and a set of transition functions, if the action is faithful, then any two fiber bundles constructed are isomorphic. To see it, use the "if" direction of the isomorphism theorem with $t_i(x)=1_G$, where $1_G\in G$ is the identity element of $G$. In other words, the construction is unique up to isomorphism.

Smooth category

The above pair of theorems hold in the topological category. A similar pair of theorems hold in the smooth category, where X and Y are smooth manifolds, G is a Lie group with a smooth left action on Y and the maps t_ij are all smooth.

Construction

Existence is proven constructively by the standard coequalizer construction in category theory.

Take the disjoint union of the product spaces $U_i\times F$

$T=\coprod _{i\in I}{U}_i\times F=\{(i,x,y):i\in I,x\in U_i,y\in F\}.$

Define the equivalence relation

$(j,x,y)\sim (i,x,t_{ij}(x)\cdot y)\mathrm{\forall }x\in U_i\cap U_j,y\in F.$

Take the quotient $E:=T/\sim$, with the projection map $$\pi :E\to X,\pi ([(i,x,y)])=x$$The local trivializations are

${\varphi }_i:{\pi }^{-1}(U_i)\to U_i\times F,{\varphi }_i^{-1}(x,y)=[(i,x,y)].$

Associated bundle

Let E → X a fiber bundle with fiber F and structure group G, and let F′ be another left G-space. One can form an associated bundle E′ → X with a fiber F′ and structure group G by taking any local trivialization of E and replacing F by F′ in the construction theorem. If one takes F′ to be G with the action of left multiplication then one obtains the associated principal bundle.

References

• Sharpe, R. W. (1997). Differential Geometry: Cartan's Generalization of Klein's Erlangen Program. New York: Springer. ISBN 0-387-94732-9. 
• Steenrod, Norman (1951). The Topology of Fibre Bundles. Princeton: Princeton University Press. ISBN 0-691-00548-6. https://archive.org/details/topologyoffibreb0000stee.  See Part I, §2.10 and §3.