Principal bundle

Short description: Fiber bundle whose fibers are group torsors

In mathematics, a principal bundle is a mathematical object that formalizes some of the essential features of the Cartesian product [math]\displaystyle{ X \times G }[/math] of a space [math]\displaystyle{ X }[/math] with a group [math]\displaystyle{ G }[/math]. In the same way as with the Cartesian product, a principal bundle [math]\displaystyle{ P }[/math] is equipped with

1. An action of [math]\displaystyle{ G }[/math] on [math]\displaystyle{ P }[/math], analogous to [math]\displaystyle{ (x, g)h = (x, gh) }[/math] for a product space.
2. A projection onto [math]\displaystyle{ X }[/math]. For a product space, this is just the projection onto the first factor, [math]\displaystyle{ (x,g) \mapsto x }[/math].

Unless it is the product space [math]\displaystyle{ X \times G }[/math], a principal bundle lacks a preferred choice of identity cross-section; it have no preferred analog of [math]\displaystyle{ x \mapsto (x,e) }[/math]. Likewise, there is not generally a projection onto [math]\displaystyle{ G }[/math] generalizing the projection onto the second factor, [math]\displaystyle{ X \times G \to G }[/math] that exists for the Cartesian product. They may also have a complicated topology that prevents them from being realized as a product space even if a number of arbitrary choices are made to try to define such a structure by defining it on smaller pieces of the space.

A common example of a principal bundle is the frame bundle [math]\displaystyle{ F(E) }[/math] of a vector bundle [math]\displaystyle{ E }[/math], which consists of all ordered bases of the vector space attached to each point. The group [math]\displaystyle{ G, }[/math] in this case, is the general linear group, which acts on the right in the usual way: by changes of basis. Since there is no natural way to choose an ordered basis of a vector space, a frame bundle lacks a canonical choice of identity cross-section.

Principal bundles have important applications in topology and differential geometry and mathematical gauge theory. They have also found application in physics where they form part of the foundational framework of physical gauge theories.

Formal definition

A principal [math]\displaystyle{ G }[/math]-bundle, where [math]\displaystyle{ G }[/math] denotes any topological group, is a fiber bundle [math]\displaystyle{ \pi:P \to X }[/math] together with a continuous right action [math]\displaystyle{ P \times G \to P }[/math] such that [math]\displaystyle{ G }[/math] preserves the fibers of [math]\displaystyle{ P }[/math] (i.e. if [math]\displaystyle{ y \in P_x }[/math] then [math]\displaystyle{ yg \in P_x }[/math] for all [math]\displaystyle{ g \in G }[/math]) and acts freely and transitively (meaning each fiber is a G-torsor) on them in such a way that for each [math]\displaystyle{ x \in X }[/math] and [math]\displaystyle{ y \in P_x }[/math], the map [math]\displaystyle{ G \to P_x }[/math] sending [math]\displaystyle{ g }[/math] to [math]\displaystyle{ yg }[/math] is a homeomorphism. In particular each fiber of the bundle is homeomorphic to the group [math]\displaystyle{ G }[/math] itself. Frequently, one requires the base space [math]\displaystyle{ X }[/math] to be Hausdorff and possibly paracompact.

Since the group action preserves the fibers of [math]\displaystyle{ \pi:P \to X }[/math] and acts transitively, it follows that the orbits of the [math]\displaystyle{ G }[/math]-action are precisely these fibers and the orbit space [math]\displaystyle{ P/G }[/math] is homeomorphic to the base space [math]\displaystyle{ X }[/math]. Because the action is free and transitive, the fibers have the structure of G-torsors. A [math]\displaystyle{ G }[/math]-torsor is a space that is homeomorphic to [math]\displaystyle{ G }[/math] but lacks a group structure since there is no preferred choice of an identity element.

An equivalent definition of a principal [math]\displaystyle{ G }[/math]-bundle is as a [math]\displaystyle{ G }[/math]-bundle [math]\displaystyle{ \pi:P \to X }[/math] with fiber [math]\displaystyle{ G }[/math] where the structure group acts on the fiber by left multiplication. Since right multiplication by [math]\displaystyle{ G }[/math] on the fiber commutes with the action of the structure group, there exists an invariant notion of right multiplication by [math]\displaystyle{ G }[/math] on [math]\displaystyle{ P }[/math]. The fibers of [math]\displaystyle{ \pi }[/math] then become right [math]\displaystyle{ G }[/math]-torsors for this action.

The definitions above are for arbitrary topological spaces. One can also define principal [math]\displaystyle{ G }[/math]-bundles in the category of smooth manifolds. Here [math]\displaystyle{ \pi:P \to X }[/math] is required to be a smooth map between smooth manifolds, [math]\displaystyle{ G }[/math] is required to be a Lie group, and the corresponding action on [math]\displaystyle{ P }[/math] should be smooth.

Examples

Trivial bundle and sections

Over an open ball [math]\displaystyle{ U \subset \mathbb{R}^n }[/math], or [math]\displaystyle{ \mathbb{R}^n }[/math], with induced coordinates [math]\displaystyle{ x_1,\ldots,x_n }[/math], any principal [math]\displaystyle{ G }[/math]-bundle is isomorphic to a trivial bundle

[math]\displaystyle{ \pi:U\times G \to U }[/math]

and a smooth section [math]\displaystyle{ s \in \Gamma(\pi) }[/math] is equivalently given by a (smooth) function [math]\displaystyle{ \hat{s}: U \to G }[/math] since

[math]\displaystyle{ s(u) = (u,\hat{s}(u)) \in U\times G }[/math]

for some smooth function. For example, if [math]\displaystyle{ G=U(2) }[/math], the Lie group of [math]\displaystyle{ 2\times 2 }[/math] unitary matrices, then a section can be constructed by considering four real-valued functions

[math]\displaystyle{ \phi(x),\psi(x),\Delta(x),\theta(x) : U \to \mathbb{R} }[/math]

and applying them to the parameterization

[math]\displaystyle{ U = e^{i\phi(x) /2}\begin{bmatrix} e^{i\psi(x)} & 0 \\ 0 & e^{-i\psi(x)} \end{bmatrix} \begin{bmatrix} \cos \theta(x) & \sin \theta(x) \\ -\sin \theta(x) & \cos \theta(x) \\ \end{bmatrix} \begin{bmatrix} e^{i\Delta(x)} & 0 \\ 0 & e^{-i\Delta(x)} \end{bmatrix}. }[/math]This same procedure by taking a parameterization of a collection of matrices defining a Lie group and by considering the set of functions from a patch to [math]\displaystyle{ \mathbb{R} }[/math] and inserting them into the parameterization.

Other examples

Non-trivial Z/2Z principal bundle over the circle. There is no well-defined way to identify which point corresponds to +1 or -1 in each fibre. This bundle is non-trivial as there is no globally defined section of the projection π.

• The prototypical example of a smooth principal bundle is the frame bundle of a smooth manifold [math]\displaystyle{ M }[/math], often denoted [math]\displaystyle{ FM }[/math] or [math]\displaystyle{ GL(M) }[/math]. Here the fiber over a point [math]\displaystyle{ x \in M }[/math] is the set of all frames (i.e. ordered bases) for the tangent space [math]\displaystyle{ T_xM }[/math]. The general linear group [math]\displaystyle{ GL(n,\mathbb{R}) }[/math] acts freely and transitively on these frames. These fibers can be glued together in a natural way so as to obtain a principal [math]\displaystyle{ GL(n,\mathbb{R}) }[/math]-bundle over [math]\displaystyle{ M }[/math].
• Variations on the above example include the orthonormal frame bundle of a Riemannian manifold. Here the frames are required to be orthonormal with respect to the metric. The structure group is the orthogonal group [math]\displaystyle{ O(n) }[/math]. The example also works for bundles other than the tangent bundle; if [math]\displaystyle{ E }[/math] is any vector bundle of rank [math]\displaystyle{ k }[/math] over [math]\displaystyle{ M }[/math], then the bundle of frames of [math]\displaystyle{ E }[/math] is a principal [math]\displaystyle{ GL(k,\mathbb{R}) }[/math]-bundle, sometimes denoted [math]\displaystyle{ F(E) }[/math].
• A normal (regular) covering space [math]\displaystyle{ p:C \to X }[/math] is a principal bundle where the structure group

[math]\displaystyle{ G = \pi_1(X)/p_{*}(\pi_1(C)) }[/math]

acts on the fibres of [math]\displaystyle{ p }[/math] via the monodromy action. In particular, the universal cover of [math]\displaystyle{ X }[/math] is a principal bundle over [math]\displaystyle{ X }[/math] with structure group [math]\displaystyle{ \pi_1(X) }[/math] (since the universal cover is simply connected and thus [math]\displaystyle{ \pi_1(C) }[/math] is trivial).

• Let [math]\displaystyle{ G }[/math] be a Lie group and let [math]\displaystyle{ H }[/math] be a closed subgroup (not necessarily normal). Then [math]\displaystyle{ G }[/math] is a principal [math]\displaystyle{ H }[/math]-bundle over the (left) coset space [math]\displaystyle{ G/H }[/math]. Here the action of [math]\displaystyle{ H }[/math] on [math]\displaystyle{ G }[/math] is just right multiplication. The fibers are the left cosets of [math]\displaystyle{ H }[/math] (in this case there is a distinguished fiber, the one containing the identity, which is naturally isomorphic to [math]\displaystyle{ H }[/math]).
• Consider the projection [math]\displaystyle{ \pi:S^1 \to S^1 }[/math] given by [math]\displaystyle{ z \mapsto z^2 }[/math]. This principal [math]\displaystyle{ \mathbb{Z}_2 }[/math]-bundle is the associated bundle of the Möbius strip. Besides the trivial bundle, this is the only principal [math]\displaystyle{ \mathbb{Z}_2 }[/math]-bundle over [math]\displaystyle{ S^1 }[/math].
• Projective spaces provide some more interesting examples of principal bundles. Recall that the [math]\displaystyle{ n }[/math]-sphere [math]\displaystyle{ S^n }[/math] is a two-fold covering space of real projective space [math]\displaystyle{ \mathbb{R}\mathbb{P}^n }[/math]. The natural action of [math]\displaystyle{ O(1) }[/math] on [math]\displaystyle{ S^n }[/math] gives it the structure of a principal [math]\displaystyle{ O(1) }[/math]-bundle over [math]\displaystyle{ \mathbb{R}\mathbb{P}^n }[/math]. Likewise, [math]\displaystyle{ S^{2n+1} }[/math] is a principal [math]\displaystyle{ U(1) }[/math]-bundle over complex projective space [math]\displaystyle{ \mathbb{C}\mathbb{P}^n }[/math] and [math]\displaystyle{ S^{4n+3} }[/math] is a principal [math]\displaystyle{ Sp(1) }[/math]-bundle over quaternionic projective space [math]\displaystyle{ \mathbb{H}\mathbb{P}^n }[/math]. We then have a series of principal bundles for each positive [math]\displaystyle{ n }[/math]:

[math]\displaystyle{ \mbox{O}(1) \to S(\mathbb{R}^{n+1}) \to \mathbb{RP}^n }[/math]

[math]\displaystyle{ \mbox{U}(1) \to S(\mathbb{C}^{n+1}) \to \mathbb{CP}^n }[/math]

[math]\displaystyle{ \mbox{Sp}(1) \to S(\mathbb{H}^{n+1}) \to \mathbb{HP}^n. }[/math]

Here [math]\displaystyle{ S(V) }[/math] denotes the unit sphere in [math]\displaystyle{ V }[/math] (equipped with the Euclidean metric). For all of these examples the [math]\displaystyle{ n = 1 }[/math] cases give the so-called Hopf bundles.

Basic properties

Trivializations and cross sections

One of the most important questions regarding any fiber bundle is whether or not it is trivial, i.e. isomorphic to a product bundle. For principal bundles there is a convenient characterization of triviality:

Proposition. A principal bundle is trivial if and only if it admits a global section.

The same is not true for other fiber bundles. For instance, vector bundles always have a zero section whether they are trivial or not and sphere bundles may admit many global sections without being trivial.

The same fact applies to local trivializations of principal bundles. Let π : P → X be a principal G-bundle. An open set U in X admits a local trivialization if and only if there exists a local section on U. Given a local trivialization

[math]\displaystyle{ \Phi : \pi^{-1}(U) \to U \times G }[/math]

one can define an associated local section

[math]\displaystyle{ s:U \to \pi^{-1}(U);s(x) = \Phi^{-1}(x,e)\, }[/math]

where e is the identity in G. Conversely, given a section s one defines a trivialization Φ by

[math]\displaystyle{ \Phi^{-1}(x,g) = s(x)\cdot g. }[/math]

The simple transitivity of the G action on the fibers of P guarantees that this map is a bijection, it is also a homeomorphism. The local trivializations defined by local sections are G-equivariant in the following sense. If we write

[math]\displaystyle{ \Phi : \pi^{-1}(U) \to U \times G }[/math]

in the form

[math]\displaystyle{ \Phi(p) = (\pi(p), \varphi(p)), }[/math]

then the map

[math]\displaystyle{ \varphi : P \to G }[/math]

satisfies

[math]\displaystyle{ \varphi(p\cdot g) = \varphi(p)g. }[/math]

Equivariant trivializations therefore preserve the G-torsor structure of the fibers. In terms of the associated local section s the map φ is given by

[math]\displaystyle{ \varphi(s(x)\cdot g) = g. }[/math]

The local version of the cross section theorem then states that the equivariant local trivializations of a principal bundle are in one-to-one correspondence with local sections.

Given an equivariant local trivialization ({U_i}, {Φ_i}) of P, we have local sections s_i on each U_i. On overlaps these must be related by the action of the structure group G. In fact, the relationship is provided by the transition functions

[math]\displaystyle{ t_{ij} : U_i \cap U_j \to G\,. }[/math]

By gluing the local trivializations together using these transition functions, one may reconstruct the original principal bundle. This is an example of the fiber bundle construction theorem. For any x ∈ U_i ∩ U_j we have

[math]\displaystyle{ s_j(x) = s_i(x)\cdot t_{ij}(x). }[/math]

Characterization of smooth principal bundles

If [math]\displaystyle{ \pi : P \to X }[/math] is a smooth principal [math]\displaystyle{ G }[/math]-bundle then [math]\displaystyle{ G }[/math] acts freely and properly on [math]\displaystyle{ P }[/math] so that the orbit space [math]\displaystyle{ P/G }[/math] is diffeomorphic to the base space [math]\displaystyle{ X }[/math]. It turns out that these properties completely characterize smooth principal bundles. That is, if [math]\displaystyle{ P }[/math] is a smooth manifold, [math]\displaystyle{ G }[/math] a Lie group and [math]\displaystyle{ \mu : P \times G \to P }[/math] a smooth, free, and proper right action then

• [math]\displaystyle{ P/G }[/math] is a smooth manifold,
• the natural projection [math]\displaystyle{ \pi : P \to P/G }[/math] is a smooth submersion, and
• [math]\displaystyle{ P }[/math] is a smooth principal [math]\displaystyle{ G }[/math]-bundle over [math]\displaystyle{ P/G }[/math].

Use of the notion

Reduction of the structure group

Given a subgroup H of G one may consider the bundle [math]\displaystyle{ P/H }[/math] whose fibers are homeomorphic to the coset space [math]\displaystyle{ G/H }[/math]. If the new bundle admits a global section, then one says that the section is a reduction of the structure group from [math]\displaystyle{ G }[/math] to [math]\displaystyle{ H }[/math] . The reason for this name is that the (fiberwise) inverse image of the values of this section form a subbundle of [math]\displaystyle{ P }[/math] that is a principal [math]\displaystyle{ H }[/math]-bundle. If [math]\displaystyle{ H }[/math] is the identity, then a section of [math]\displaystyle{ P }[/math] itself is a reduction of the structure group to the identity. Reductions of the structure group do not in general exist.

Many topological questions about the structure of a manifold or the structure of bundles over it that are associated to a principal [math]\displaystyle{ G }[/math]-bundle may be rephrased as questions about the admissibility of the reduction of the structure group (from [math]\displaystyle{ G }[/math] to [math]\displaystyle{ H }[/math]). For example:

The frame bundle [math]\displaystyle{ \mathcal{F}(E) }[/math] of the Möbius strip [math]\displaystyle{ E }[/math] is a non-trivial principal [math]\displaystyle{ \mathbb{Z}/2\mathbb{Z} }[/math]-bundle over the circle.

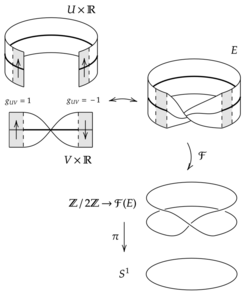
• A [math]\displaystyle{ 2n }[/math]-dimensional real manifold admits an almost-complex structure if the frame bundle on the manifold, whose fibers are [math]\displaystyle{ GL(2n,\mathbb{R}) }[/math], can be reduced to the group [math]\displaystyle{ \mathrm{GL}(n,\mathbb{C}) \subseteq \mathrm{GL}(2n,\mathbb{R}) }[/math].
• An [math]\displaystyle{ n }[/math]-dimensional real manifold admits a [math]\displaystyle{ k }[/math]-plane field if the frame bundle can be reduced to the structure group [math]\displaystyle{ \mathrm{GL}(k,\mathbb{R}) \subseteq \mathrm{GL}(n,\mathbb{R}) }[/math].
• A manifold is orientable if and only if its frame bundle can be reduced to the special orthogonal group, [math]\displaystyle{ \mathrm{SO}(n) \subseteq \mathrm{GL}(n,\mathbb{R}) }[/math].
• A manifold has spin structure if and only if its frame bundle can be further reduced from [math]\displaystyle{ \mathrm{SO}(n) }[/math] to [math]\displaystyle{ \mathrm{Spin}(n) }[/math] the Spin group, which maps to [math]\displaystyle{ \mathrm{SO}(n) }[/math] as a double cover.

Also note: an [math]\displaystyle{ n }[/math]-dimensional manifold admits [math]\displaystyle{ n }[/math] vector fields that are linearly independent at each point if and only if its frame bundle admits a global section. In this case, the manifold is called parallelizable.

Associated vector bundles and frames

If [math]\displaystyle{ P }[/math] is a principal [math]\displaystyle{ G }[/math]-bundle and [math]\displaystyle{ V }[/math] is a linear representation of [math]\displaystyle{ G }[/math], then one can construct a vector bundle [math]\displaystyle{ E=P\times_G V }[/math] with fibre [math]\displaystyle{ V }[/math], as the quotient of the product [math]\displaystyle{ P }[/math]×[math]\displaystyle{ V }[/math] by the diagonal action of [math]\displaystyle{ G }[/math]. This is a special case of the associated bundle construction, and [math]\displaystyle{ E }[/math] is called an associated vector bundle to [math]\displaystyle{ P }[/math]. If the representation of [math]\displaystyle{ G }[/math] on [math]\displaystyle{ V }[/math] is faithful, so that [math]\displaystyle{ G }[/math] is a subgroup of the general linear group GL([math]\displaystyle{ V }[/math]), then [math]\displaystyle{ E }[/math] is a [math]\displaystyle{ G }[/math]-bundle and [math]\displaystyle{ P }[/math] provides a reduction of structure group of the frame bundle of [math]\displaystyle{ E }[/math] from [math]\displaystyle{ GL(V) }[/math] to [math]\displaystyle{ G }[/math]. This is the sense in which principal bundles provide an abstract formulation of the theory of frame bundles.

Classification of principal bundles

Any topological group G admits a classifying space BG: the quotient by the action of G of some weakly contractible space, e.g., a topological space with vanishing homotopy groups. The classifying space has the property that any G principal bundle over a paracompact manifold B is isomorphic to a pullback of the principal bundle EG → BG. In fact, more is true, as the set of isomorphism classes of principal G bundles over the base B identifies with the set of homotopy classes of maps B → BG.

See also

• Associated bundle
• Vector bundle
• G-structure
• Reduction of the structure group
• Gauge theory
• Connection (principal bundle)
• G-fibration

Sources

• Bleecker, David (1981). Gauge Theory and Variational Principles. Addison-Wesley Publishing. ISBN 0-486-44546-1. https://archive.org/details/gaugetheoryvaria00blee_0. 
• Jost, Jürgen (2005). Riemannian Geometry and Geometric Analysis ((4th ed.) ed.). New York: Springer. ISBN 3-540-25907-4. 
• Husemoller, Dale (1994). Fibre Bundles (Third ed.). New York: Springer. ISBN 978-0-387-94087-8. 
• Sharpe, R. W. (1997). Differential Geometry: Cartan's Generalization of Klein's Erlangen Program. New York: Springer. ISBN 0-387-94732-9. 
• Steenrod, Norman (1951). The Topology of Fibre Bundles. Princeton: Princeton University Press. ISBN 0-691-00548-6. https://archive.org/details/topologyoffibreb0000stee.