Edmonds–Karp algorithm

Short description: Algorithm to compute the maximum flow in a flow network

In computer science, the Edmonds–Karp algorithm is an implementation of the Ford–Fulkerson method for computing the maximum flow in a flow network in [math]\displaystyle{ O(|V||E|^2) }[/math] time. The algorithm was first published by Yefim Dinitz in 1970, and independently published by Jack Edmonds and Richard Karp in 1972. Dinitz's algorithm includes additional techniques that reduce the running time to [math]\displaystyle{ O(|V|^2|E|) }[/math].

Algorithm

The algorithm is identical to the Ford–Fulkerson algorithm, except that the search order when finding the augmenting path is defined. The path found must be a shortest path that has available capacity. This can be found by a breadth-first search, where we apply a weight of 1 to each edge. The running time of [math]\displaystyle{ O(|V||E|^2) }[/math] is found by showing that each augmenting path can be found in [math]\displaystyle{ O(|E|) }[/math] time, that every time at least one of the [math]\displaystyle{ E }[/math] edges becomes saturated (an edge which has the maximum possible flow), that the distance from the saturated edge to the source along the augmenting path must be longer than last time it was saturated, and that the length is at most [math]\displaystyle{ |V| }[/math]. Another property of this algorithm is that the length of the shortest augmenting path increases monotonically. There is an accessible proof in Introduction to Algorithms.

Pseudocode

algorithm EdmondsKarp is
    input:
        graph   (graph[v] should be the list of edges coming out of vertex v in the
                 original graph and their corresponding constructed reverse edges
                 which are used for push-back flow.
                 Each edge should have a capacity 'cap', flow, source 's' and sink 't' 
                 as parameters, as well as a pointer to the reverse edge 'rev'.)
        s       (Source vertex)
        t       (Sink vertex)
    output:
        flow    (Value of maximum flow)
    
    flow := 0   (Initialize flow to zero)
    repeat
        (Run a breadth-first search (bfs) to find the shortest s-t path.
         We use 'pred' to store the edge taken to get to each vertex,
         so we can recover the path afterwards)
        q := queue()
        q.push(s)
        pred := array(graph.length)
        while not empty(q) and pred[t] = null
            cur := q.pop()
            for Edge e in graph[cur] do
                if pred[e.t] = null and e.t ≠ s and e.cap > e.flow then
                    pred[e.t] := e
                    q.push(e.t)

        if not (pred[t] = null) then
            (We found an augmenting path.
             See how much flow we can send) 
            df := ∞
            for (e := pred[t]; e ≠ null; e := pred[e.s]) do
                df := min(df, e.cap - e.flow)
            (And update edges by that amount)
            for (e := pred[t]; e ≠ null; e := pred[e.s]) do
                e.flow  := e.flow + df
                e.rev.flow := e.rev.flow - df
            flow := flow + df

    until pred[t] = null  (i.e., until no augmenting path was found)
    return flow

Example

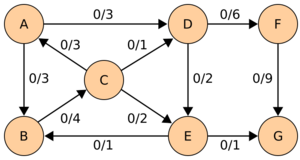
Given a network of seven nodes, source A, sink G, and capacities as shown below:

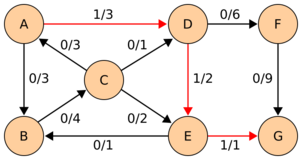
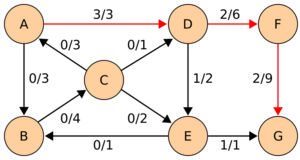
In the pairs [math]\displaystyle{ f/c }[/math] written on the edges, [math]\displaystyle{ f }[/math] is the current flow, and [math]\displaystyle{ c }[/math] is the capacity. The residual capacity from [math]\displaystyle{ u }[/math] to [math]\displaystyle{ v }[/math] is [math]\displaystyle{ c_f(u,v)=c(u,v)-f(u,v) }[/math], the total capacity, minus the flow that is already used. If the net flow from [math]\displaystyle{ u }[/math] to [math]\displaystyle{ v }[/math] is negative, it contributes to the residual capacity.

Capacity	Path	Resulting network
[math]\displaystyle{ \begin{align} & \min(c_f(A,D),c_f(D,E),c_f(E,G)) \\ = & \min(3-0,2-0,1-0) = \\ = & \min(3,2,1) = 1 \end{align} }[/math]	[math]\displaystyle{ A,D,E,G }[/math]
[math]\displaystyle{ \begin{align} & \min(c_f(A,D),c_f(D,F),c_f(F,G)) \\ = & \min(3-1,6-0,9-0) \\ = & \min(2,6,9) = 2 \end{align} }[/math]	[math]\displaystyle{ A,D,F,G }[/math]
[math]\displaystyle{ \begin{align} & \min(c_f(A,B),c_f(B,C),c_f(C,D),c_f(D,F),c_f(F,G)) \\ = & \min(3-0,4-0,1-0,6-2,9-2) \\ = & \min(3,4,1,4,7) = 1 \end{align} }[/math]	[math]\displaystyle{ A,B,C,D,F,G }[/math]
[math]\displaystyle{ \begin{align} & \min(c_f(A,B),c_f(B,C),c_f(C,E),c_f(E,D),c_f(D,F),c_f(F,G)) \\ = & \min(3-1,4-1,2-0,0-(-1),6-3,9-3) \\ = & \min(2,3,2,1,3,6) = 1 \end{align} }[/math]	[math]\displaystyle{ A,B,C,E,D,F,G }[/math]

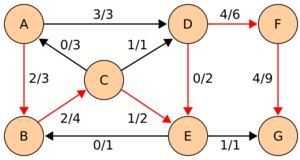
Notice how the length of the augmenting path found by the algorithm (in red) never decreases. The paths found are the shortest possible. The flow found is equal to the capacity across the minimum cut in the graph separating the source and the sink. There is only one minimal cut in this graph, partitioning the nodes into the sets [math]\displaystyle{ \{A,B,C,E\} }[/math] and [math]\displaystyle{ \{D,F,G\} }[/math], with the capacity

[math]\displaystyle{ c(A,D)+c(C,D)+c(E,G)=3+1+1=5.\ }[/math]

References

1. Algorithms and Complexity (see pages 63–69). https://web.archive.org/web/20061005083406/http://www.cis.upenn.edu/~wilf/AlgComp3.html