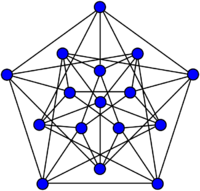
Frankl–Rödl graph
In graph theory and computational complexity theory, a Frankl–Rödl graph is a graph defined by connecting pairs of vertices of a hypercube that are at a specified even distance from each other. The graphs of this type are parameterized by the dimension of the hypercube and by the distance between adjacent vertices.
Frankl–Rödl graphs are named after Péter Frankl and Vojtěch Rödl, who proved in 1987 that (for certain ranges of the graph parameters) they have small independence number and high chromatic number.[1] They have since become of interest to computational complexity theorists, as difficult examples for semidefinite programming based approximation algorithms for the vertex cover and graph coloring problems. Their properties with respect to these algorithms have been used to call into question the unique games conjecture.
Definition and examples
Let n be a positive integer, and let γ be a real number in the unit interval 0 ≤ γ ≤ 1. Suppose additionally that (1 − γ)n is an even number. Then the Frankl–Rödl graph [math]\displaystyle{ \operatorname{FR}_{\gamma}^{n} }[/math] is the graph on the 2n vertices of an n-dimensional unit hypercube [0,1]n in which two vertices are adjacent when their Hamming distance (the number of coordinates in which the two differ) is exactly (1 − γ)n.[2] Here, the requirement that (1 − γ)n be even is necessary in order to prevent the result from being a bipartite graph. The Frankl–Rödl graph will necessarily be disconnected (with at least one connected component for each of the two sides of the bipartition of the corresponding hypercube graph) but this is non-problematic for its applications.
As an example, the Frankl–Rödl graph [math]\displaystyle{ \operatorname{FR}_{1/3}^{3} }[/math] connects vertices two steps apart in an ordinary three-dimensional cube, as shown in the illustration. Geometrically, this connection pattern forms a shape known as the stella octangula; graph-theoretically, it forms two connected components, each of which is a four-vertex complete graph. Similarly, the Frankl–Rödl graph [math]\displaystyle{ \operatorname{FR}_{1/2}^{4} }[/math] connects vertices two steps apart in a four-dimensional hypercube, and results in a graph consisting of two copies of the cocktail party graph K2,2,2,2. The two Frankl–Rödl graphs of dimension five, [math]\displaystyle{ \operatorname{FR}_{1/5}^{5} }[/math] and [math]\displaystyle{ \operatorname{FR}_{3/5}^{5} }[/math], are each formed from two copies of the two complementary Clebsch graphs of degree five and ten respectively.
Properties
The Frankl–Rödl graph [math]\displaystyle{ \operatorname{FR}_{\gamma}^{n} }[/math] is a regular graph, of degree
- [math]\displaystyle{ \binom{n}{(1-\gamma)n}. }[/math]
It inherits the symmetries of its underlying hypercube, making it a symmetric graph.
As (Frankl Rödl) showed,[3] when γ ≤ 1/4, the size of a maximum independent set in a Frankl–Rödl graph [math]\displaystyle{ \operatorname{FR}_{\gamma}^{n} }[/math] is
- [math]\displaystyle{ n(2-\Omega(\gamma)^2)^n. }[/math]
The Ω in this formula is an instance of big Ω notation. For constant values of γ and variable n, this independent set size is a small fraction of the 2n vertices of the graph. More precisely, this fraction is inversely proportional to an exponential function of n and a polynomial function of the graph size. Because each color in proper coloring of the Frankl–Rödl graph forms an independent set with few vertices, the number of colors must be large (again, a polynomial function of the graph size).
In computational complexity
The vertex cover problem involves finding a set of vertices that touches every edge of the graph. It is NP-hard but can be approximated to within an approximation ratio of two, for instance by taking the endpoints of the matched edges in any maximal matching. Evidence that this is the best possible approximation ratio of a polynomial-time approximation algorithm is provided by the fact that, when represented as a semidefinite program, the problem has an integrality gap of two; this gap is the ratio between the solution value of the integer solution (a valid vertex cover) and of its semidefinite relaxation. According to the unique games conjecture, for many problems such as this the optimal approximation ratio is provided by the integrality gap of their semidefinite relaxation. However, the Frankl–Rödl graphs provide the only known instances of vertex cover for which the integrality gap can be as bad as two.[4]
Frankl–Rödl graphs have also been used to study semidefinite approximations for graph coloring. In this application, in particular, researchers have studied graph 3-colorability in connection with the Frankl–Rödl graphs with parameter γ = 1/4. Even though the Frankl–Rödl graphs with this parameter value have high chromatic number, semidefinite programming is unable to distinguish them from 3-colorable graphs.[5][6][7] However, for these graphs, algebraic methods based on polynomial sums of squares can provide stronger bounds that certify their need for many colors. This result challenges the optimality of semidefinite programming and the correctness of the unique games conjecture.[2]
References
- ↑ "Forbidden intersections", Transactions of the American Mathematical Society 300 (1): 259–286, 1987, doi:10.2307/2000598.
- ↑ 2.0 2.1 Tan, Li-Yang; Zhou, Yuan; O'Donnell, Ryan (2016), "Hypercontractive inequalities via SOS, and the Frankl–Rödl graph", Discrete Analysis 2016:4: 20pp, doi:10.19086/da.612.
- ↑ See also Georgiou, Konstantinos (2010), "Integrality gaps of 2 − o(1) for vertex cover SDPs in the Lovász–Schrijver hierarchy", SIAM Journal on Computing 39 (8): 3553–3570, doi:10.1137/080721479, http://www.cs.toronto.edu/~toni/Papers/vc.pdf.
- ↑ (Georgiou Magen); (Tan Zhou).
- ↑ "Approximate graph coloring by semidefinite programming", Journal of the ACM 45 (2): 246–265, 1998, doi:10.1145/274787.274791.
- ↑ "The Lovász theta function and a semidefinite programming relaxation of vertex cover", SIAM Journal on Discrete Mathematics 11 (2): 196–204, 1998, doi:10.1137/S0895480195287541.
- ↑ Charikar, Moses (2002), "On semidefinite programming relaxations for graph coloring and vertex cover", Proceedings of the Thirteenth Annual ACM-SIAM Symposium on Discrete Algorithms (SODA '02), Philadelphia, PA, USA: Society for Industrial and Applied Mathematics, pp. 616–620, ISBN 978-0-89871-513-2, http://dl.acm.org/citation.cfm?id=545381.545462.
 |