Clebsch graph
| Clebsch graph | |
|---|---|
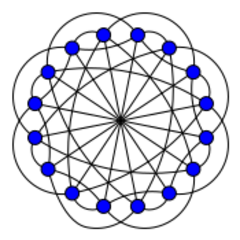 | |
| Named after | Alfred Clebsch |
| Vertices | 16 |
| Edges | 40 |
| Radius | 2 |
| Diameter | 2 |
| Girth | 4 |
| Automorphisms | 1920 |
| Chromatic number | 4[1] |
| Chromatic index | 5 |
| Book thickness | 4 |
| Queue number | 3 |
| Properties | Strongly regular Hamiltonian Cayley graph Vertex-transitive Edge-transitive Distance-transitive. |
| Table of graphs and parameters | |
In the mathematical field of graph theory, the Clebsch graph is either of two complementary graphs on 16 vertices, a 5-regular graph with 40 edges and a 10-regular graph with 80 edges. The 80-edge graph is the dimension-5 halved cube graph; it was called the Clebsch graph name by Seidel (1968)[2] because of its relation to the configuration of 16 lines on the quartic surface discovered in 1868 by the German mathematician Alfred Clebsch. The 40-edge variant is the dimension-5 folded cube graph; it is also known as the Greenwood–Gleason graph after the work of Robert E. Greenwood and Andrew M. Gleason (1955), who used it to evaluate the Ramsey number R(3,3,3) = 17.[3][4][5]
Construction
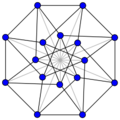
The dimension-5 folded cube graph (the 5-regular Clebsch graph) may be constructed by adding edges between opposite pairs of vertices in a 4-dimensional hypercube graph. (In an n-dimensional hypercube, a pair of vertices are opposite if the shortest path between them has n edges.) Alternatively, it can be formed from a 5-dimensional hypercube graph by identifying together (or contracting) every opposite pair of vertices.
Another construction, leading to the same graph, is to create a vertex for each element of the finite field GF(16), and connect two vertices by an edge whenever the difference between the corresponding two field elements is a perfect cube.[6]
The dimension-5 halved cube graph (the 10-regular Clebsch graph) is the complement of the 5-regular graph. It may also be constructed from the vertices of a 5-dimensional hypercube, by connecting pairs of vertices whose Hamming distance is exactly two. This construction is an instance of the construction of Frankl–Rödl graphs. It produces two subsets of 16 vertices that are disconnected from each other; both of these half-squares of the hypercube are isomorphic to the 10-regular Clebsch graph. Two copies of the 5-regular Clebsch graph can be produced in the same way from a 5-dimensional hypercube, by connecting pairs of vertices whose Hamming distance is exactly four.
Properties
The 5-regular Clebsch graph is a strongly regular graph of degree 5 with parameters .[7][8] Its complement, the 10-regular Clebsch graph, is therefore also a strongly regular graph,[1][4] with parameters .
The 5-regular Clebsch graph is Hamiltonian, non planar and non Eulerian. It is also both 5-vertex-connected and 5-edge-connected. The subgraph that is induced by the ten non-neighbors of any vertex in this graph forms an isomorphic copy of the Petersen graph.
It has book thickness 4 and queue number 3.[9]

The edges of the complete graph K16 may be partitioned into three disjoint copies of the 5-regular Clebsch graph. Because the Clebsch graph is a triangle-free graph, this shows that there is a triangle-free three-coloring of the edges of K16; that is, that the Ramsey number R(3,3,3) describing the minimum number of vertices in a complete graph without a triangle-free three-coloring is at least 17. (Greenwood Gleason) used this construction as part of their proof that R(3,3,3) = 17.[5][10]
The 5-regular Clebsch graph may be colored with four colors, but not three: its largest independent set has five vertices, not enough to partition the graph into three independent color classes. It contains as an induced subgraph the Grötzsch graph, the smallest triangle-free four-chromatic graph, and every four-chromatic induced subgraph of the Clebsch graph is a supergraph of the Grötzsch graph. More strongly, every triangle-free four-chromatic graph with no induced path of length six or more is an induced subgraph of the Clebsch graph and an induced supergraph of the Grötzsch graph.[11]
The 5-regular Clebsch graph is the Keller graph of dimension two, part of a family of graphs used to find tilings of high-dimensional Euclidean spaces by hypercubes no two of which meet face-to-face.
The 5-regular Clebsch graph can be embedded as a regular map in the orientable manifold of genus 5, forming pentagonal faces; and in the non-orientable surface of genus 6, forming tetragonal faces.
Algebraic properties
The characteristic polynomial of the 5-regular Clebsch graph is . Because this polynomial can be completely factored into linear terms with integer coefficients, the Clebsch graph is an integral graph: its spectrum consists entirely of integers.[4] The Clebsch graph is the only graph with this characteristic polynomial, making it a graph determined by its spectrum.
The 5-regular Clebsch graph is a Cayley graph with an automorphism group of order 1920, isomorphic to the Coxeter group . As a Cayley graph, its automorphism group acts transitively on its vertices, making it vertex transitive. In fact, it is arc transitive, hence edge transitive and distance transitive. It is also connected-homogeneous, meaning that every isomorphism between two connected induced subgraphs can be extended to an automorphism of the whole graph.
Gallery
-
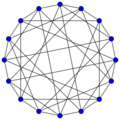
The Clebsch graph is Hamiltonian.
-
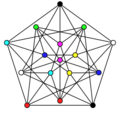
The achromatic number of the Clebsch graph is 8.
-
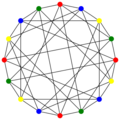
The chromatic number of the Clebsch graph is 4.
-
The chromatic index of the Clebsch graph is 5.
-
Construction of the Clebsch graph from a hypercube graph.
References
- ↑ 1.0 1.1 Weisstein, Eric W.. "Clebsch Graph.". From MathWorld—A Wolfram Web Resource. http://mathworld.wolfram.com/ClebschGraph.html. Retrieved 2009-08-13.
- ↑ J. J. Seidel, Strongly regular graphs with (−1,1,0) adjacency matrix having eigenvalue 3, Lin. Alg. Appl. 1 (1968) 281-298.
- ↑ Clebsch, A. (1868), "Ueber die Flächen vierter Ordnung, welche eine Doppelcurve zweiten Grades besitzen", Journal für die reine und angewandte Mathematik 69: 142–184.
- ↑ 4.0 4.1 4.2 "The Clebsch Graph on Bill Cherowitzo's home page". http://www-math.ucdenver.edu/~wcherowi/courses/m6023/shilpa.pdf.
- ↑ 5.0 5.1 Greenwood, R. E. (1955), "Combinatorial relations and chromatic graphs", Canadian Journal of Mathematics 7: 1–7, doi:10.4153/CJM-1955-001-4.
- ↑ De Clerck, Frank (1997). "Constructions and Characterizations of (Semi)partial Geometries". p. 6. http://cage.ugent.be/~fdc/potenza.ps.
- ↑ Godsil, C.D. (1995). "Problems in algebraic combinatorics". Electronic Journal of Combinatorics 2: 3. doi:10.37236/1224. http://www.combinatorics.org/Volume_2/PDFFiles/v2i1f1.pdf. Retrieved 2009-08-13.
- ↑ Peter J. Cameron Strongly regular graphs on DesignTheory.org, 2001
- ↑ Jessica Wolz, Engineering Linear Layouts with SAT. Master Thesis, University of Tübingen, 2018
- ↑ Sun, Hugo S.; Cohen, M. E. (1984), "An easy proof of the Greenwood–Gleason evaluation of the Ramsey number R(3,3,3)", The Fibonacci Quarterly 22 (3): 235–238, http://www.fq.math.ca/Scanned/22-3/sun.pdf.
- ↑ Randerath, Bert; Schiermeyer, Ingo; Tewes, Meike (2002), "Three-colourability and forbidden subgraphs. II. Polynomial algorithms", Discrete Mathematics 251 (1–3): 137–153, doi:10.1016/S0012-365X(01)00335-1.
 |